2021-2022学年浙教版九年级数学上册1.4 二次函数的应用同步检测(word版附答案)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册1.4 二次函数的应用同步检测(word版附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 18:51:11 | ||
图片预览




文档简介
1.4
二次函数的应用
一、选择题(共4小题;共20分)
1.
下列有关函数
的说法中,正确的是
A.
有最大值
B.
有最大值
,但没有最小值
C.
没有最大值,但有最小值
D.
既有最大值
,又有最小值
2.
烟花厂为扬州“烟花三月经贸旅游节”特别设计制作一种新型礼炮,这种礼炮的升空高度
关于飞行时间
的表达式是
.若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为
A.
B.
C.
D.
3.
将进货单价为
元的某种商品按零售价
元一个售出时,每天能卖出
个.若这种商品的零售价在一定范围内每降价
元,其日销售量就增加
个.为了获得最大利润,则应降价
A.
元
B.
元
C.
元
D.
元
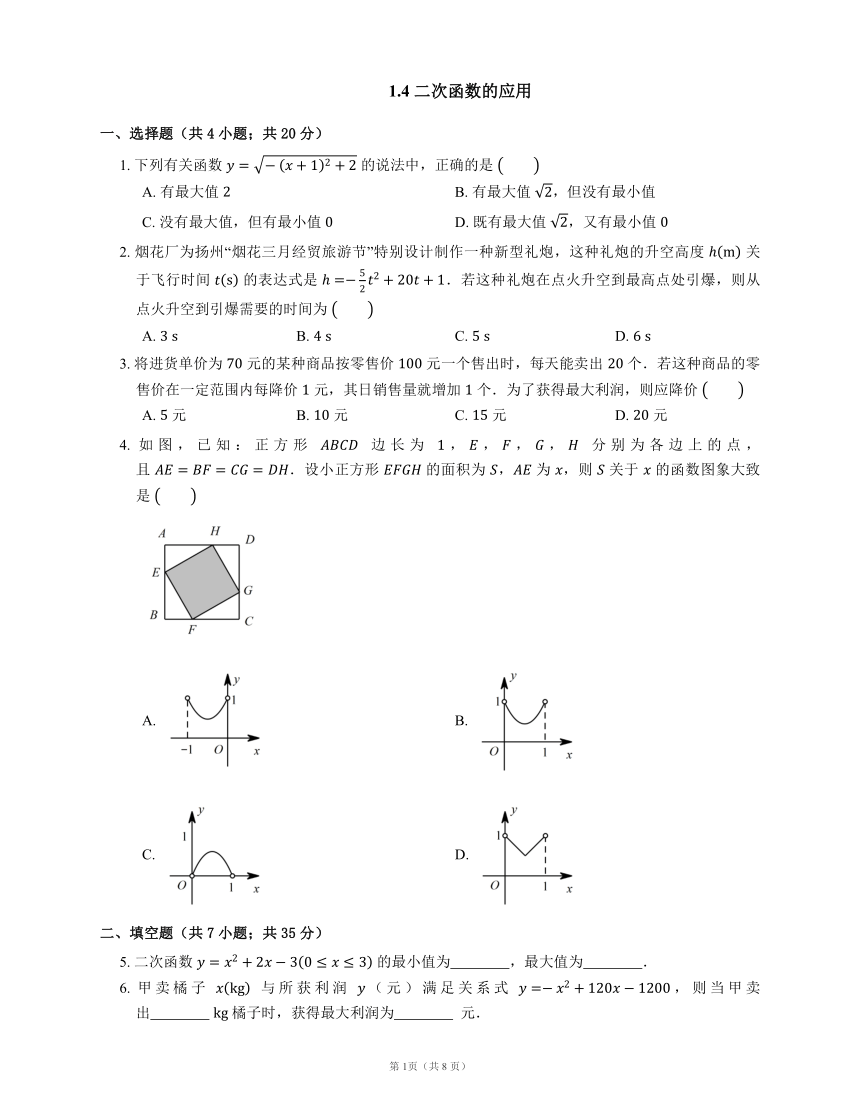
4.
如图,已知:正方形
边长为
,,,,
分别为各边上的点,且
.设小正方形
的面积为
,
为
,则
关于
的函数图象大致是
A.
B.
C.
D.
二、填空题(共7小题;共35分)
5.
二次函数
的最小值为
?,最大值为
?.
6.
甲卖橘子
与所获利润
(元)满足关系式
,则当甲卖出
?
橘子时,获得最大利润为
?
元.
7.
已知函数
,则当
?
时,
取最大值为
?.
8.
如图,
是抛物线
在第一象限上的点,过点
分别向
轴和
轴作垂线,垂足分别为点
,点
,则四边形
周长的最大值为
?.
9.
某种火箭被竖直向上发射时,它的高度
与时间
的关系可以用公式
表示.经过
?
,火箭达到它的最高点.
10.
将一条长为
的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是
?
.
11.
出售某种手工艺品,若每个获利
元,一天可售出
个,则当
?
元,一天出售该种手工艺品的总利润
最大.
三、解答题(共7小题;12,18题各15分,13-17题各13分,共95分)
12.
如图,在
中,,,,两个动点
,
同时从
点出发,点
沿
匀速运动,点
沿
匀速运动,两点同时到达点
.
(1)点
的速度是点
速度的多少倍?
(2)设
,
的面积是
,求
关于
的函数表达式,并写出
的取值范围;
(3)求出
的最大值.
13.
如图,正方形纸片
的边长是
,点
,
分别在
和
上(其中点
不与点
重合),沿直线
折叠该纸片,点
恰好落在
边上点
处.
(1)设
,四边形
的面积为
,求
关于
的函数表达式,并写出
的取值范围;
(2)当
为何值时,四边形
的面积最大?最大值是多少?
14.
某商品的进价为每件
元.当售价为每件
元时,每星期可卖出
件,现需降价处理,且经市场调查:每降价
元,每星期可多卖出
件.在确保盈利的前提下,解答下列问题;
(1)若设每件降价
元,每星期售出商品的利润为
元,请写出
与
的函数表达式,并求出自变量
的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
15.
甲船和乙船分别从
港和
港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是
和
,且
,
两港之间的距离为
.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少(注:题中的“距离”都指直线距离,图中
)?
16.
如图,抛物线的对称轴为直线
,抛物线与
轴交于
,
两点,与
轴交于点
,,.若点
是此抛物线位于
轴上方的一个动点,求
面积的最大值.
17.
某大型酒店有包房
间,在每天晚餐营业时间,每间包房收费
元时,包房便可全部租出;若每间包房收费提高
元,则减少
间包房租出;若每间包房收费再提高
元,则再减少
间包房租出,以每次提高
元的这种方式变化下去.
(1)设每间包房收费提高
(元),则每间包房的收入为
(元),但会减少
间包房租出,请直接写出
,
与
之间的函数表达式;
(2)为了投资少而利润大,每间包房提高
(元)后,设酒店老板每天晚餐包房总收入为
(元),请写出
与
之间的函数表达式,求出每间包房每天晚餐营业时间应提高多少元可获得最大包房费收入,并说明理由.
18.
某商场试销一种成本为每件
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
,经试销发现,销售量
(
件)与销售单价
(元)符合一次函数
,且
时,;
时,.
(1)求一次函数
的表达式;
(2)若该商场获得利润为
元,试写出利润
与销售单价
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于
元,试确定销售单价
的范围.
答案
1.
D
2.
B
3.
A
4.
B
5.
,
6.
,
7.
,
8.
9.
10.
11.
【解析】提示:.
12.
(1)
在
中,,,,
,,而两个动点
,
同时从
点出发,点
沿
匀速运动,点
沿
匀速运动,两点同时到达点
,
的速度是
的速度的
倍.
??????(2)
设
,
的面积是
.
①当
在
上,即
时,;
②当
在
上,即
时,,即:.
??????(3)
对于
,当
时,;
对于
,当
时,.
,
当
时,.
13.
(1)
连接
,,
依题意,点
和点
关于
对称,
则
,由勾股定理得:,
得
,
作
于点
,则
,
且
,
因为
,
所以
,
又因为
,
所以
,
在
和
中,
,,,
所以
,
所以
,,
所以
其中
.
??????(2)
因为
,
所以当
时,,此时,,
所以当
时,四边形
的面积最大,最大值为
.
14.
(1)
,.
??????(2)
,
当降价
元时,每星期的利润最大,最大利润是
元.
15.
设经过
后快艇和轮船之间的距离最短,最短距离是
,
由题意可得,,
当
时,
取得最小值为
,也就是经过
,甲船和乙船之间的距离最短,最短距离为
.
16.
由对称性可知
,,
时,,得
,
所以
,
所以
的最大值为
.
17.
(1)
,.
??????(2)
,即
,
提价前包房费总收入为
,当
时,可获最大包房收入
元,
.
又
每次提价为
元,
每间包房晚餐营业时间应提高
元或
元.
18.
(1)
由题意得
解得
.
??????(2)
.
抛物线的开口向下,
当
时,
随
的增大而增大,
,
当
时,
有最大值
.
当销售单价定为
元时,商场可获得最大利润,最大利润是
元.
??????(3)
当
时,,
.
.
第1页(共7
页)
二次函数的应用
一、选择题(共4小题;共20分)
1.
下列有关函数
的说法中,正确的是
A.
有最大值
B.
有最大值
,但没有最小值
C.
没有最大值,但有最小值
D.
既有最大值
,又有最小值
2.
烟花厂为扬州“烟花三月经贸旅游节”特别设计制作一种新型礼炮,这种礼炮的升空高度
关于飞行时间
的表达式是
.若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为
A.
B.
C.
D.
3.
将进货单价为
元的某种商品按零售价
元一个售出时,每天能卖出
个.若这种商品的零售价在一定范围内每降价
元,其日销售量就增加
个.为了获得最大利润,则应降价
A.
元
B.
元
C.
元
D.
元
4.
如图,已知:正方形
边长为
,,,,
分别为各边上的点,且
.设小正方形
的面积为
,
为
,则
关于
的函数图象大致是
A.
B.
C.
D.
二、填空题(共7小题;共35分)
5.
二次函数
的最小值为
?,最大值为
?.
6.
甲卖橘子
与所获利润
(元)满足关系式
,则当甲卖出
?
橘子时,获得最大利润为
?
元.
7.
已知函数
,则当
?
时,
取最大值为
?.
8.
如图,
是抛物线
在第一象限上的点,过点
分别向
轴和
轴作垂线,垂足分别为点
,点
,则四边形
周长的最大值为
?.
9.
某种火箭被竖直向上发射时,它的高度
与时间
的关系可以用公式
表示.经过
?
,火箭达到它的最高点.
10.
将一条长为
的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是
?
.
11.
出售某种手工艺品,若每个获利
元,一天可售出
个,则当
?
元,一天出售该种手工艺品的总利润
最大.
三、解答题(共7小题;12,18题各15分,13-17题各13分,共95分)
12.
如图,在
中,,,,两个动点
,
同时从
点出发,点
沿
匀速运动,点
沿
匀速运动,两点同时到达点
.
(1)点
的速度是点
速度的多少倍?
(2)设
,
的面积是
,求
关于
的函数表达式,并写出
的取值范围;
(3)求出
的最大值.
13.
如图,正方形纸片
的边长是
,点
,
分别在
和
上(其中点
不与点
重合),沿直线
折叠该纸片,点
恰好落在
边上点
处.
(1)设
,四边形
的面积为
,求
关于
的函数表达式,并写出
的取值范围;
(2)当
为何值时,四边形
的面积最大?最大值是多少?
14.
某商品的进价为每件
元.当售价为每件
元时,每星期可卖出
件,现需降价处理,且经市场调查:每降价
元,每星期可多卖出
件.在确保盈利的前提下,解答下列问题;
(1)若设每件降价
元,每星期售出商品的利润为
元,请写出
与
的函数表达式,并求出自变量
的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
15.
甲船和乙船分别从
港和
港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是
和
,且
,
两港之间的距离为
.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少(注:题中的“距离”都指直线距离,图中
)?
16.
如图,抛物线的对称轴为直线
,抛物线与
轴交于
,
两点,与
轴交于点
,,.若点
是此抛物线位于
轴上方的一个动点,求
面积的最大值.
17.
某大型酒店有包房
间,在每天晚餐营业时间,每间包房收费
元时,包房便可全部租出;若每间包房收费提高
元,则减少
间包房租出;若每间包房收费再提高
元,则再减少
间包房租出,以每次提高
元的这种方式变化下去.
(1)设每间包房收费提高
(元),则每间包房的收入为
(元),但会减少
间包房租出,请直接写出
,
与
之间的函数表达式;
(2)为了投资少而利润大,每间包房提高
(元)后,设酒店老板每天晚餐包房总收入为
(元),请写出
与
之间的函数表达式,求出每间包房每天晚餐营业时间应提高多少元可获得最大包房费收入,并说明理由.
18.
某商场试销一种成本为每件
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
,经试销发现,销售量
(
件)与销售单价
(元)符合一次函数
,且
时,;
时,.
(1)求一次函数
的表达式;
(2)若该商场获得利润为
元,试写出利润
与销售单价
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于
元,试确定销售单价
的范围.
答案
1.
D
2.
B
3.
A
4.
B
5.
,
6.
,
7.
,
8.
9.
10.
11.
【解析】提示:.
12.
(1)
在
中,,,,
,,而两个动点
,
同时从
点出发,点
沿
匀速运动,点
沿
匀速运动,两点同时到达点
,
的速度是
的速度的
倍.
??????(2)
设
,
的面积是
.
①当
在
上,即
时,;
②当
在
上,即
时,,即:.
??????(3)
对于
,当
时,;
对于
,当
时,.
,
当
时,.
13.
(1)
连接
,,
依题意,点
和点
关于
对称,
则
,由勾股定理得:,
得
,
作
于点
,则
,
且
,
因为
,
所以
,
又因为
,
所以
,
在
和
中,
,,,
所以
,
所以
,,
所以
其中
.
??????(2)
因为
,
所以当
时,,此时,,
所以当
时,四边形
的面积最大,最大值为
.
14.
(1)
,.
??????(2)
,
当降价
元时,每星期的利润最大,最大利润是
元.
15.
设经过
后快艇和轮船之间的距离最短,最短距离是
,
由题意可得,,
当
时,
取得最小值为
,也就是经过
,甲船和乙船之间的距离最短,最短距离为
.
16.
由对称性可知
,,
时,,得
,
所以
,
所以
的最大值为
.
17.
(1)
,.
??????(2)
,即
,
提价前包房费总收入为
,当
时,可获最大包房收入
元,
.
又
每次提价为
元,
每间包房晚餐营业时间应提高
元或
元.
18.
(1)
由题意得
解得
.
??????(2)
.
抛物线的开口向下,
当
时,
随
的增大而增大,
,
当
时,
有最大值
.
当销售单价定为
元时,商场可获得最大利润,最大利润是
元.
??????(3)
当
时,,
.
.
第1页(共7
页)
同课章节目录
