1.1二次函数 同步练习（含答案）

中小学教育资源及组卷应用平台
浙教版九上数学-二次函数
一、单选题
1.（2019八下·鼓楼期末）已知二次函数y＝ax2+bx+c的x与y的部分对应值如下表：
x
…
﹣3
﹣2
﹣1
0
1
3
…
y
…
﹣27
﹣13
﹣3
3
5
﹣3
…
下列结论：①a＜0；②方程ax2+bx+c＝3的解为x1＝0，x2＝2；③当x＞2时，y＜0．
其中所有正确结论的序号是（　　）
A.?①②③?????????????????????????????????????B.?①?????????????????????????????????????C.?②③?????????????????????????????????????D.?①②
2.如图，一段抛物线：y=﹣x（x﹣5）（0≤x≤5），记为C1
，
它与x轴交于点O，A1；将C1绕点A1旋转180°得C2
，
交x轴于点A2；将C2绕点A2旋转180°得C3
，
交x轴于点A3；…如此进行下去，得到一“波浪线”，若点P（2018，m）在此“波浪线”上，则m的值为（?
?）
A.?4?????????????????????????????????????????B.?﹣4?????????????????????????????????????????C.?﹣6?????????????????????????????????????????D.?6
3.（2019九上·河东期中）二次函数
的部分图象如图所示，图象过点
，对称轴为直线
，
下列结论：
①
；
②
；
③
；
④若点
，点
，点
在该函数图象上，则
；
⑤若方程
的两根为
和
，且
，则
.
其中正确的结论有（???
）
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
4.如图，OABC是边长为1的正方形，OC与x轴正半轴的夹角为15°，点B在抛物线y=ax2（a＜0）的图象上，则a的值为?（　??　）??
?
A.????????????????????????????????????????B.?-2??????????????????????????????????????C.?-???????????????????????????????????????D.??
二、填空题
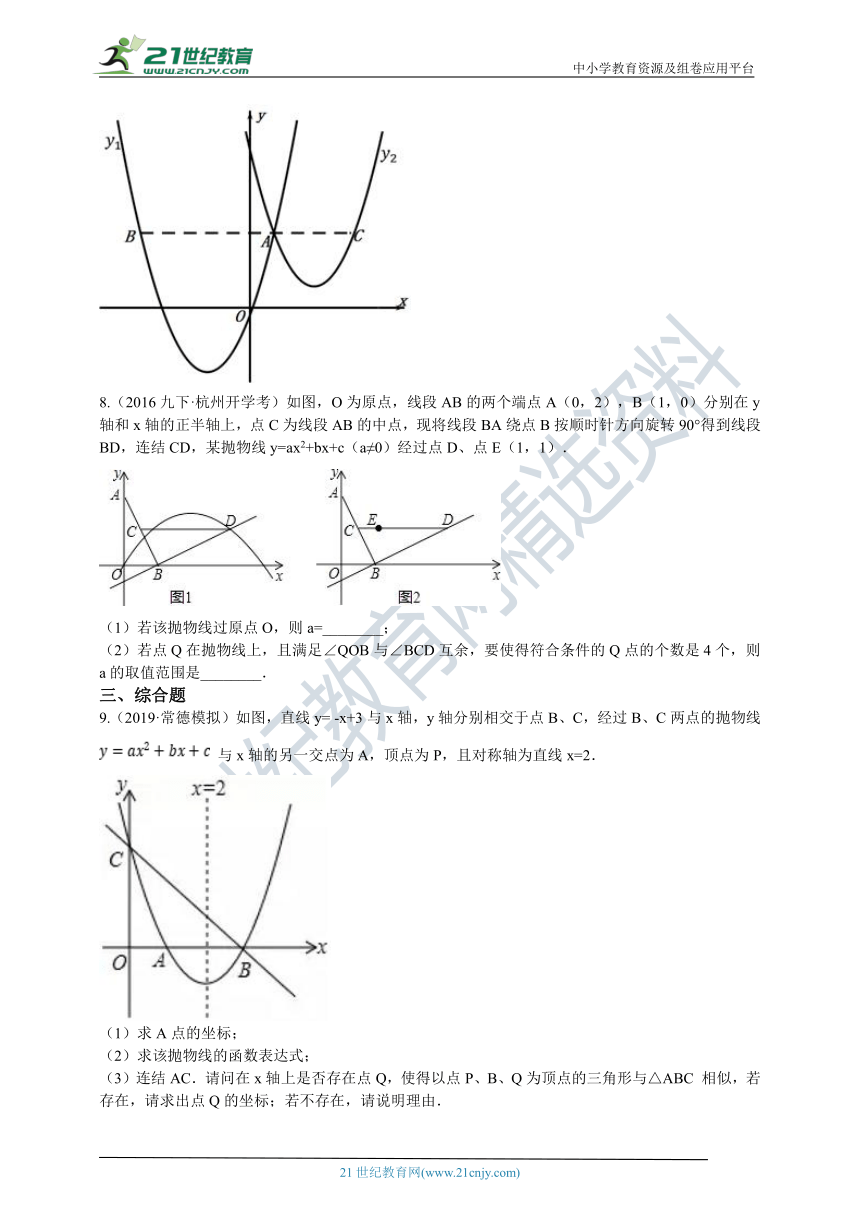
5.（2018九上·重庆月考）如图，平行于x轴的直线AC分别交函数y1＝x2（x≥0）与y2＝
（x≥0）的图象于B、C两点，过点C作y轴的平行线交y1的图象于点D，直线DE∥AC，交y2的图象于点E，则
＝________.
6.（2020·淄博）某快递公司在甲地和乙地之间共设有29个服务驿站（包括甲站、乙站），一辆快递货车由甲站出发，依次途经各站驶往乙站，每停靠一站，均要卸下前面各站发往该站的货包各1个，又要装上该站发往后面各站的货包各1个．在整个行程中，快递货车装载的货包数量最多是________个．
7.（2020九上·广汉期中）如图，抛物线
与
交于点
，过点
作
轴的平行线，分别交两条抛物线于点
，
．则以下结论：①无论
取何值，
2的值总是正数；②
；③当
时，
；④
．其中正确结论是________．
8.（2016九下·杭州开学考）如图，O为原点，线段AB的两个端点A（0，2），B（1，0）分别在y轴和x轴的正半轴上，点C为线段AB的中点，现将线段BA绕点B按顺时针方向旋转90°得到线段BD，连结CD，某抛物线y=ax2+bx+c（a≠0）经过点D、点E（1，1）．
（1）若该抛物线过原点O，则a=________；
（2）若点Q在抛物线上，且满足∠QOB与∠BCD互余，要使得符合条件的Q点的个数是4个，则a的取值范围是________．
三、综合题
9.（2019·常德模拟）如图，直线y=
-x+3与x轴，y轴分别相交于点B、C，经过B、C两点的抛物线
与x轴的另一交点为A，顶点为P，且对称轴为直线x=2．
（1）求A点的坐标；
（2）求该抛物线的函数表达式；
（3）连结AC．请问在x轴上是否存在点Q，使得以点P、B、Q为顶点的三角形与△ABC
相似，若存在，请求出点Q的坐标；若不存在，请说明理由．
10.（2018·宁波模拟）抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（
，0），且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．
11.（2019·义乌模拟）如图1，矩形OABC中，OA＝3，OC＝2，以矩形的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系.在直线OA上取一点D，将△BDA沿BD翻折，点A的对应点为点A'，直线DA'与直线BC的交点为F.
（1）如图2，当点A′恰好落在线段CB上时，取AB的中点E，
①直接写出点E、F的坐标；
②设顶点为F的抛物线交y轴正半轴于点P，且以点E、F、P为顶点的三角形是等腰三角形，求该抛物线的解析式；
③在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由.
（2）在平面内找一点G，连结BG、FG，使四边形A'BGF为正方形，求点D的坐标.
12.（2019九上·温州开学考）如图
，直线
与x轴、y轴分别交于点B，C，抛物线
过B，C两点，且与x轴的另一个交点为点A，连接AC．
（1）求抛物线的解析式；
（2）在抛物线上是否存在点
与点A不重合
，使得
，若存在，求出点D的坐标；若不存在，请说明理由；
（3）有宽度为2，长度足够长的矩形
阴影部分
沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线CB于点M和点N，在矩形平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．
13.（2019九上·凤山期末）如图，直线y=x+3与两坐标轴交于A，B两点，抛物线y=x2+bx+c过A、B两点，且交x轴的正半轴于点C。
（1）直接写出A、B两点的坐标；
（2）求抛物线的解析式和顶点D的坐标；
（3）在抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形?若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．
答案解析部分
一、单选题
1.【答案】
D
2.【答案】
C
3.【答案】
B
4.【答案】
C
二、填空题
5.【答案】
3-
6.【答案】
210
7.【答案】
①④
8.【答案】
（1）﹣
（2）a＜﹣
或a＞
三、综合题
9.【答案】
（1）解：∵直线y=-x+3与x轴相交于点B，
∴当y=0时，x=3，
∴点B的坐标为（3，0）．
又∵抛物线过x轴上的A，B两点，且对称轴为x=2，
根据抛物线的对称性，
∴点A的坐标为（1，0）．
（2）解：∵y=-x+3过点C，易知C（0，3），
∴c=3．
又∵抛物线y=ax2+bx+c过点A（1，0），B（3，0），
，解，得
，
∴y=x2-4x+3．
（3）解：连接PB，由y=x2-4x+3=（x-2）2-1，得P（2，-1），
设抛物线的对称轴交x轴于点M，
∵在Rt△PBM中，PM=MB=1，
，
由点B（3，0），C（0，3）易得OB=OC=3，
在等腰直角三角形OBC中，∠ABC=45°，
由勾股定理，得
，
假设在x轴上存在点Q，使得以点P，B，Q为顶点的三角形与△ABC相似．
①当
时，△PBQ∽△ABC．
即
∴BQ=3，
又∵BO=3，
∴点Q与点O重合，
∴Q1的坐标是（0，0）．
②当
，△QBP∽△ABC．
即
，
，
∵OB=3，
，
∴Q2的坐标是
.
∵∠PBQ=180°-45°=135°，∠BAC＜135°，
∴∠PBQ≠∠BAC．
∴点Q不可能在B点右侧的x轴上
综上所述，在x轴上存在两点
，
能使得以点P，B，Q为顶点的三角形与△ABC相似．
10.【答案】
（1）解：由题意，得
解得
．
∴这条抛物线的表达式为
．
（2）解：作BH⊥AC于点H，∵A点坐标是（－1，0），C点坐标是（0，3），B点坐标是（
，0），∴AC=
，AB=
，OC=3，BC=
．∵
，即
，∴
．Rt△
BCH中，
，BC=
，∠BHC=90?，∴
．
又∵∠ACB是锐角，∴
（3）解：延长CD交x轴于点G，
∵Rt△
AOC中，AO=1，AC=
，
∴
．
∵△DCE∽△AOC，∴只可能∠CAO=∠DCE．
∴AG
=
CG．
∴
．
∴AG=5．∴G点坐标是（4，0）．
∵点C坐标是（0，3），∴
．
∴
?解得
，
（舍）.
∴点D坐标是
11.【答案】
（1）解：①∵矩形OABC中，OA＝3，OC＝2
∴∠BAO＝∠ABC＝90°，AB＝OC＝2，BC＝OA＝3
∴B(3，2)
∵E为AB中点
∴E(3，1)
∵△BDA沿BD翻折得△BDA'，点A'落在BC边上的F处，
∴∠BA'D＝∠BAD＝90°，AD＝A'D
∴四边形ABA'D是正方形
∴A'D＝AD＝A'B＝AB＝2
∴A'C＝BC﹣A'B＝1
∴F(1，2)
②∵抛物线顶点F(1，2)，
∴设抛物线解析式为y＝a(x﹣1)2+2(a≠0)
在Rt△EBF中，∠EBF＝90°，BE＝1，BF＝2
∴EF＝
设点P的坐标为(0，n)，其中n＞0
i)如图1，当EF＝PF时，PF2＝EF2＝5
∴12+(n﹣2)2＝5
解得：n1＝0(舍去)；n2＝4
∴P(0，4)
∴4＝a(0﹣1)2+2
解得：a＝2
∴抛物线的解析式为y＝2(x﹣1)2+2
ii)如图2，当EP＝FP时，EP2＝FP2
，
∴(2﹣n)2+1＝(1﹣n)2+32
解得：n＝-
(舍去)
iii)当EF＝EP时，EP＝
，这种情况不存在.
综上所述，符合条件的抛物线解析式是y＝2(x﹣1)2+2.
③存在点M，N，使得四边形MNFE的周长最小.
如图3，作点E关于x轴的对称点E′，作点F关于y轴的对称点F′，
连接E′F′，分别与x轴、y轴交于点M，N，则点M，N就是所求点
∴E′(3，﹣1)，F′(﹣1，2)，NF＝NF′，ME＝ME′
∴BF′＝4，BE′＝3
∴FN+NM+ME＝F′N+NM+ME′＝E′F′＝
∵EF＝
∴FN+MN+ME+EF＝5+
∴四边形MNFE的周长最小值是5+
（2）解：如图4，过点A'作MN⊥x轴于点N，交BC于点M
∴MN⊥BC，∠A'ND＝90°，四边形OCMN是矩形
∴ON＝CM，MN＝OC＝2
∵四边形A'BGF是正方形
∴A'F＝A'B＝AB＝2
∴BF＝
∴A'M＝BM＝FM＝
BF＝
∴ON＝CM＝BC﹣BM＝3﹣
，A'N＝MN﹣A'M＝2﹣
∵∠A'DN＝∠A'FM＝45°
∴DN＝A'N＝2﹣
∴OD＝ON+DN＝
∴点D坐标为(5﹣2
，0)
12.【答案】
（1）解：由题意C（0，-3），B（6，0），
把C（0，-3），B（6，0）代入y=
+bx+c得到
，
解得
，
∴抛物线的解析式为y=
x2-x-3．
（2）解：如图①中，作AD∥BC交抛物线于D，则S△ABC=S△BCD
．
∵直线BC的解析式为y=
x-3，A（-2，0），
∴直线AD的解析式为y=
x+1，
由
，解得
或
，
∴D（8，5）．
∵直线AD交y轴于E（0，1），
点E关于点C的对称点E′（0，-7），
∴过点E′平行BC的直线的解析式为y=
x-7，
由
，方程组无解，
∴在直线BC的下方不存在满足条件的点D．
∴满足条件的点D（8，5）．
（3）解：设M（m，
m-3），则N（m+2，
m-2），
∴P（m，
m2-m-3），Q[m+2，
（m+2）2-（m+2）-3]，
∴PM=
m-3-（
m2-m-3），NQ=
m-2-[
（m+2）2-（m+2）-3]，
当PM=QN时，点P，Q，M，N为顶点的四边形是平行四边形，
∴|
m-3-（
m2-m-3）|=|
m-2-[
（m+2）2-（m+2）-3]|，
解得：m=2或2±2
，
∴满足条件的点M的坐标为（2，-2）或（2+2
，
-2）或（2-2
，-
-2）
13.【答案】
（1）解：当x=0时，y=3，∴B(0，3)，
当y=0时，x+3=0，x=-3，∴A(-3，0)．
（2）解：把A(-3，0)，B(0，3)分别代入y=-x2+bx+a得：
，解得：
，
∴抛物线解析式为：y=-x2-2x+3．
配方得：y=-(x+1)2+4?
∴顶点D坐标为(-1，4)．
（3）解：存在，设点P的坐标为(x，-x2-2x+3)
∵A(-3，0)，B(0，3)，∴AB2=32+32=18，
AP2=(x+3)2+(-x2-2x+3)2
，
BP2=x2+(-x2-2x)2
当△PAB是以AB为直角边的直角三角形时，可分两种情况：
如图1，
如果点B为直角顶点，那么AB2+BP2=AP2
即18+x2+(-x2-2x)2=(x+3)2+(-x2-2x+3)2
整理得x2+x=0，解得x1=-1，???
x2=0(不合题意舍去)，
则点P的坐标为(-1，4)．
如图2，
如果点A为直角顶点，那么AP2+AB2=BP2
，
即18+(x+3)2+(-x2-2x+3)2=x2+(-x2-2x)2
，
整理得x2+x-6=0，解得x1=2，???
x2=-3(不合题意舍去)，
则点P的坐标为(2，-5)
综上所述，所有符合条件的点P的坐标为(-1，4)或(2，-5)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)