2021-2022学年浙教版版九年级数学上册同步练习附答案:1.2 二次函数的图象
文档属性
| 名称 | 2021-2022学年浙教版版九年级数学上册同步练习附答案:1.2 二次函数的图象 |  | |
| 格式 | zip | ||
| 文件大小 | 525.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:25:07 | ||
图片预览


文档简介
1.2
二次函数的图象
一、选择题(共8小题;共40分)
1.
如果将抛物线
向右平移
个单位,那么所得的抛物线的二次函数的表达式为
A.
B.
C.
D.
2.
二次函数
的图象如图所示,则一次函数
的图象不经过
A.
第四象限
B.
第三象限
C.
第二象限
D.
第一象限
3.
如图所示,抛物线
与直线
交于点
,沿直线
平移抛物线,使得平移后的抛物线顶点恰好为点
,则平移后抛物线的二次函数的表达式为
A.
B.
C.
D.
4.
图象的顶点为
,且经过原点的抛物线的函数表达式为
A.
B.
C.
D.
5.
已知
,,
为实数,且二次函数
在坐标平面内的图形经过
,
两点.若
,,则
的值为
A.
B.
C.
D.
6.
将抛物线
向左平移
个单位,得到的抛物线与
轴的交点坐标是
A.
B.
C.
D.
7.
将抛物线
向右平移
个单位,再向上平移
个单位后,抛物线的函数表达式为
A.
B.
C.
D.
8.
函数
与
在同一平面直角坐标系中的图象可能是
A.
B.
C.
D.
二、填空题(共9小题;共45分)
9.
把二次函数
用配方法化成
的形式是
?,该二次函数图象的顶点坐标是
?.
10.
如果二次函数
的图象经过点
和
,那么
的值为
?.
11.
已知抛物线
,当
时,
?(填“”或“”).
12.
如果抛物线
经过
,
两点,那么
的值是
?.
13.
如图所示,在平面直角坐标系中,抛物线
经过平移得到抛物线
,其对称轴与两条抛物线所围成的阴影部分的面积为
?.
14.
二次函数
的图象如图所示,已知
,,则该抛物线的函数表达式为
?(用顶点式表示).
15.
已知抛物线
的顶点在
轴上,则
?.
16.
如图所示,一段抛物线
与
轴交于点
,;将
向右平移得第
段抛物线
,交
轴于点
,;再将
向右平移得第
段抛物线
交
轴于点
,;又将
向右平移得第
段抛物线
,交
轴于点
,,若
在
上,则
的值是
?.
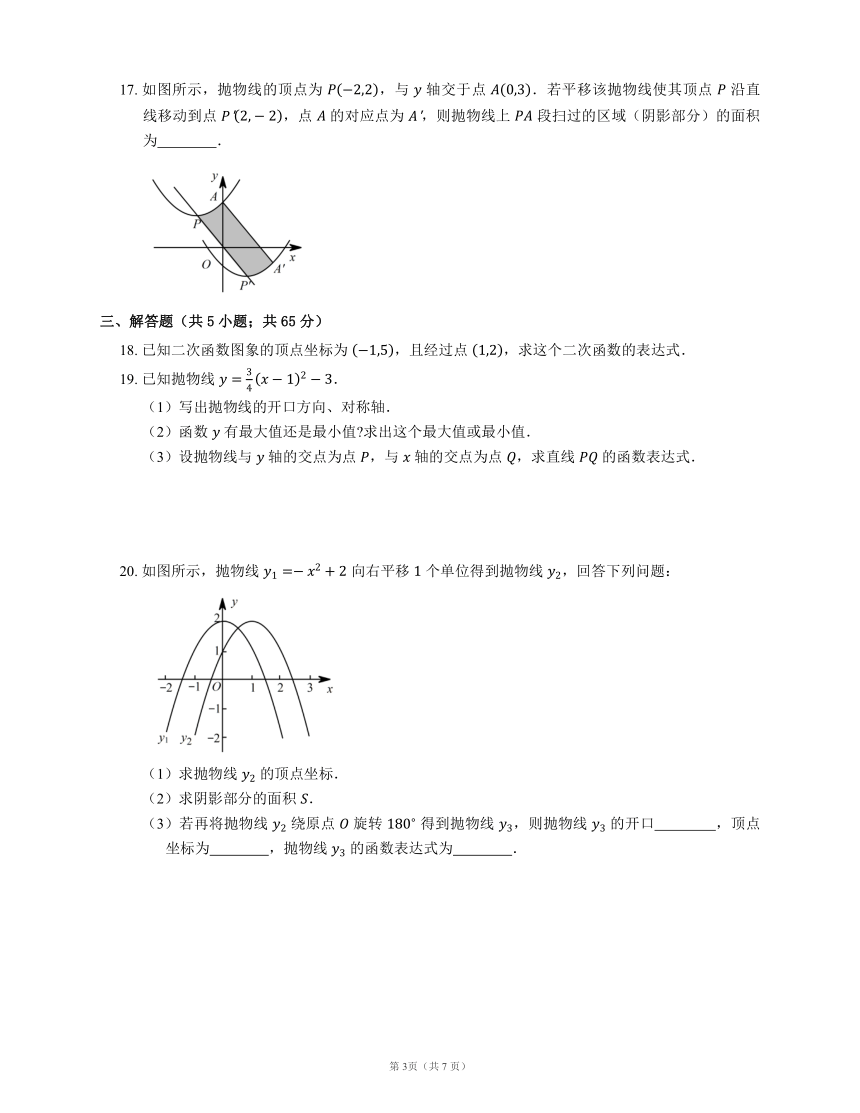
17.
如图所示,抛物线的顶点为
,与
轴交于点
.若平移该抛物线使其顶点
沿直线移动到点
,点
的对应点为
,则抛物线上
段扫过的区域(阴影部分)的面积为
?.
三、解答题(共5小题;共65分)
18.
已知二次函数图象的顶点坐标为
,且经过点
,求这个二次函数的表达式.
19.
已知抛物线
.
(1)写出抛物线的开口方向、对称轴.
(2)函数
有最大值还是最小值?求出这个最大值或最小值.
(3)设抛物线与
轴的交点为点
,与
轴的交点为点
,求直线
的函数表达式.
20.
如图所示,抛物线
向右平移
个单位得到抛物线
,回答下列问题:
(1)求抛物线
的顶点坐标.
(2)求阴影部分的面积
.
(3)若再将抛物线
绕原点
旋转
得到抛物线
,则抛物线
的开口
?,顶点坐标为
?,抛物线
的函数表达式为
?.
21.
已知抛物线
(,
是常数,且
,)的顶点在直线
上,且经过点
.
(1)求这条抛物线的函数表达式.
(2)将此抛物线沿
轴翻折得到抛物线
,求
的函数表达式.
22.
如图所示,直线
与
轴、
轴分别交于点
,,抛物线
经过点
,,并与
轴交于另一点
,其顶点为
.
(1)求
,
的值.
(2)抛物线的对称轴上有一点
,使
是以
为底边的等腰三角形,求点
的坐标.
(3)在抛物线及其对称轴上分别取点
,,使以
,,,
为顶点的四边形为正方形,求此正方形的边长.
答案
1.
C
2.
D
3.
C
4.
A
5.
D
6.
B
7.
B
【解析】根据抛物线的平移规律“左加右减,上加下减“可得答案.
8.
B
9.
,
10.
11.
12.
13.
14.
15.
或
16.
17.
18.
设这个二次函数的表达式为
.将点
代入,得
,解得
.
.
19.
(1)
开口向上,对称轴为直线
.
??????(2)
有最小值.当
时,最小值为
.
??????(3)
与
轴的交点为
,与
轴的交点为
或
.
①当
,
时,直线
的函数表达式为
;
②当
,
时,直线
的函数表达式为
.
20.
(1)
的函数表达式为
,
所以顶点坐标为
.
??????(2)
在第一象限中,将阴影部分去掉,通过平移可得
的正方形方格,
所以阴影部分面积
.
??????(3)
向上;;
21.
(1)
将顶点
代入
,得
,
所求抛物线的函数表达式为
,
将点
代入,得
.
抛物线的函数表达式为
.
??????(2)
.
22.
(1)
因为直线
与
轴、
轴分别交于点
,,
所以
,.
因为抛物线
经过点
,,
所以
解得
所以
,
的值分别为
,.
??????(2)
如图
1
所示,
设点
的坐标为
,对称轴直线
交
轴于点
,过点
作
垂直于直线
于点
.
在
中,,
在
中,.
因为
.
所以
.
所以
.
所以点
的坐标为
.
??????(3)
如图
2所示,
因为当点
在对称轴上时,
与
不垂直,
所以点
应为正方形的对角线.
因为对称轴直线
是
的中垂线,
所以点
与顶点
重合.点
为点
关于
轴的对称点,其坐标为
.此时,,且
,
所以四边形
为正方形.
在
中,.
即正方形的边长为
.
第1页(共7
页)
二次函数的图象
一、选择题(共8小题;共40分)
1.
如果将抛物线
向右平移
个单位,那么所得的抛物线的二次函数的表达式为
A.
B.
C.
D.
2.
二次函数
的图象如图所示,则一次函数
的图象不经过
A.
第四象限
B.
第三象限
C.
第二象限
D.
第一象限
3.
如图所示,抛物线
与直线
交于点
,沿直线
平移抛物线,使得平移后的抛物线顶点恰好为点
,则平移后抛物线的二次函数的表达式为
A.
B.
C.
D.
4.
图象的顶点为
,且经过原点的抛物线的函数表达式为
A.
B.
C.
D.
5.
已知
,,
为实数,且二次函数
在坐标平面内的图形经过
,
两点.若
,,则
的值为
A.
B.
C.
D.
6.
将抛物线
向左平移
个单位,得到的抛物线与
轴的交点坐标是
A.
B.
C.
D.
7.
将抛物线
向右平移
个单位,再向上平移
个单位后,抛物线的函数表达式为
A.
B.
C.
D.
8.
函数
与
在同一平面直角坐标系中的图象可能是
A.
B.
C.
D.
二、填空题(共9小题;共45分)
9.
把二次函数
用配方法化成
的形式是
?,该二次函数图象的顶点坐标是
?.
10.
如果二次函数
的图象经过点
和
,那么
的值为
?.
11.
已知抛物线
,当
时,
?(填“”或“”).
12.
如果抛物线
经过
,
两点,那么
的值是
?.
13.
如图所示,在平面直角坐标系中,抛物线
经过平移得到抛物线
,其对称轴与两条抛物线所围成的阴影部分的面积为
?.
14.
二次函数
的图象如图所示,已知
,,则该抛物线的函数表达式为
?(用顶点式表示).
15.
已知抛物线
的顶点在
轴上,则
?.
16.
如图所示,一段抛物线
与
轴交于点
,;将
向右平移得第
段抛物线
,交
轴于点
,;再将
向右平移得第
段抛物线
交
轴于点
,;又将
向右平移得第
段抛物线
,交
轴于点
,,若
在
上,则
的值是
?.
17.
如图所示,抛物线的顶点为
,与
轴交于点
.若平移该抛物线使其顶点
沿直线移动到点
,点
的对应点为
,则抛物线上
段扫过的区域(阴影部分)的面积为
?.
三、解答题(共5小题;共65分)
18.
已知二次函数图象的顶点坐标为
,且经过点
,求这个二次函数的表达式.
19.
已知抛物线
.
(1)写出抛物线的开口方向、对称轴.
(2)函数
有最大值还是最小值?求出这个最大值或最小值.
(3)设抛物线与
轴的交点为点
,与
轴的交点为点
,求直线
的函数表达式.
20.
如图所示,抛物线
向右平移
个单位得到抛物线
,回答下列问题:
(1)求抛物线
的顶点坐标.
(2)求阴影部分的面积
.
(3)若再将抛物线
绕原点
旋转
得到抛物线
,则抛物线
的开口
?,顶点坐标为
?,抛物线
的函数表达式为
?.
21.
已知抛物线
(,
是常数,且
,)的顶点在直线
上,且经过点
.
(1)求这条抛物线的函数表达式.
(2)将此抛物线沿
轴翻折得到抛物线
,求
的函数表达式.
22.
如图所示,直线
与
轴、
轴分别交于点
,,抛物线
经过点
,,并与
轴交于另一点
,其顶点为
.
(1)求
,
的值.
(2)抛物线的对称轴上有一点
,使
是以
为底边的等腰三角形,求点
的坐标.
(3)在抛物线及其对称轴上分别取点
,,使以
,,,
为顶点的四边形为正方形,求此正方形的边长.
答案
1.
C
2.
D
3.
C
4.
A
5.
D
6.
B
7.
B
【解析】根据抛物线的平移规律“左加右减,上加下减“可得答案.
8.
B
9.
,
10.
11.
12.
13.
14.
15.
或
16.
17.
18.
设这个二次函数的表达式为
.将点
代入,得
,解得
.
.
19.
(1)
开口向上,对称轴为直线
.
??????(2)
有最小值.当
时,最小值为
.
??????(3)
与
轴的交点为
,与
轴的交点为
或
.
①当
,
时,直线
的函数表达式为
;
②当
,
时,直线
的函数表达式为
.
20.
(1)
的函数表达式为
,
所以顶点坐标为
.
??????(2)
在第一象限中,将阴影部分去掉,通过平移可得
的正方形方格,
所以阴影部分面积
.
??????(3)
向上;;
21.
(1)
将顶点
代入
,得
,
所求抛物线的函数表达式为
,
将点
代入,得
.
抛物线的函数表达式为
.
??????(2)
.
22.
(1)
因为直线
与
轴、
轴分别交于点
,,
所以
,.
因为抛物线
经过点
,,
所以
解得
所以
,
的值分别为
,.
??????(2)
如图
1
所示,
设点
的坐标为
,对称轴直线
交
轴于点
,过点
作
垂直于直线
于点
.
在
中,,
在
中,.
因为
.
所以
.
所以
.
所以点
的坐标为
.
??????(3)
如图
2所示,
因为当点
在对称轴上时,
与
不垂直,
所以点
应为正方形的对角线.
因为对称轴直线
是
的中垂线,
所以点
与顶点
重合.点
为点
关于
轴的对称点,其坐标为
.此时,,且
,
所以四边形
为正方形.
在
中,.
即正方形的边长为
.
第1页(共7
页)
同课章节目录
