2021-2022学年浙教版版九年级数学上册同步练习附答案:1.4 二次函数的应用第1课时 利用二次函数解决面积最值问题
文档属性
| 名称 | 2021-2022学年浙教版版九年级数学上册同步练习附答案:1.4 二次函数的应用第1课时 利用二次函数解决面积最值问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 301.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:27:13 | ||
图片预览

文档简介
1.4
二次函数的应用第1课时
利用二次函数解决面积最值问题
一、选择题(共4小题;共20分)
1.
用一根长为
的绳子围成一个矩形,其面积的最大值为
A.
B.
C.
D.
2.
如果二次函数
的最小值为负数,则
的取值范围是
A.
B.
C.
D.
3.
某广场有一喷水池,水从地面喷出,如图,以水平地面为
轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线
(单位:)的一部分,则水喷出的最大高度是
A.
B.
C.
D.
4.
向上发射一枚炮弹,经
后的高度为
,且时间与高度的关系为
,若此炮弹在第
秒与第
秒时的高度相等,则下列时间中,高度最高的是
A.
第
秒
B.
第
秒
C.
第
秒
D.
第
秒
二、填空题(共8小题;共40分)
5.
运用二次函数求实际问题中的最大值或最小值,首先应当求出函数
?
和自变量的
?,然后通过
?,或利用
?
求它的
?,取得最大值或最小值对应的自变量的值必须在
?
内.
6.
二次函数
,当
?
时,
有最
?
值,这个值是
?.
7.
设矩形窗户的周长为
,则窗户面积
与窗户宽
之间的函数表达式是
?,自变量
的取值范围是
?.
8.
正方形的边长为
,若边长增加
,那么面积增加
,则
关于
的函数表达式为
?.
9.
若两数的和为
,则这两个数的积最大可达到
?.
10.
函数
的最小值是
?,最大值是
?.
11.
如图,用
长的木条(厚度忽略不计),做一个有一条横档的矩形窗子框架,为使透进的光线最多,应选择窗子的长、宽各为
?
.
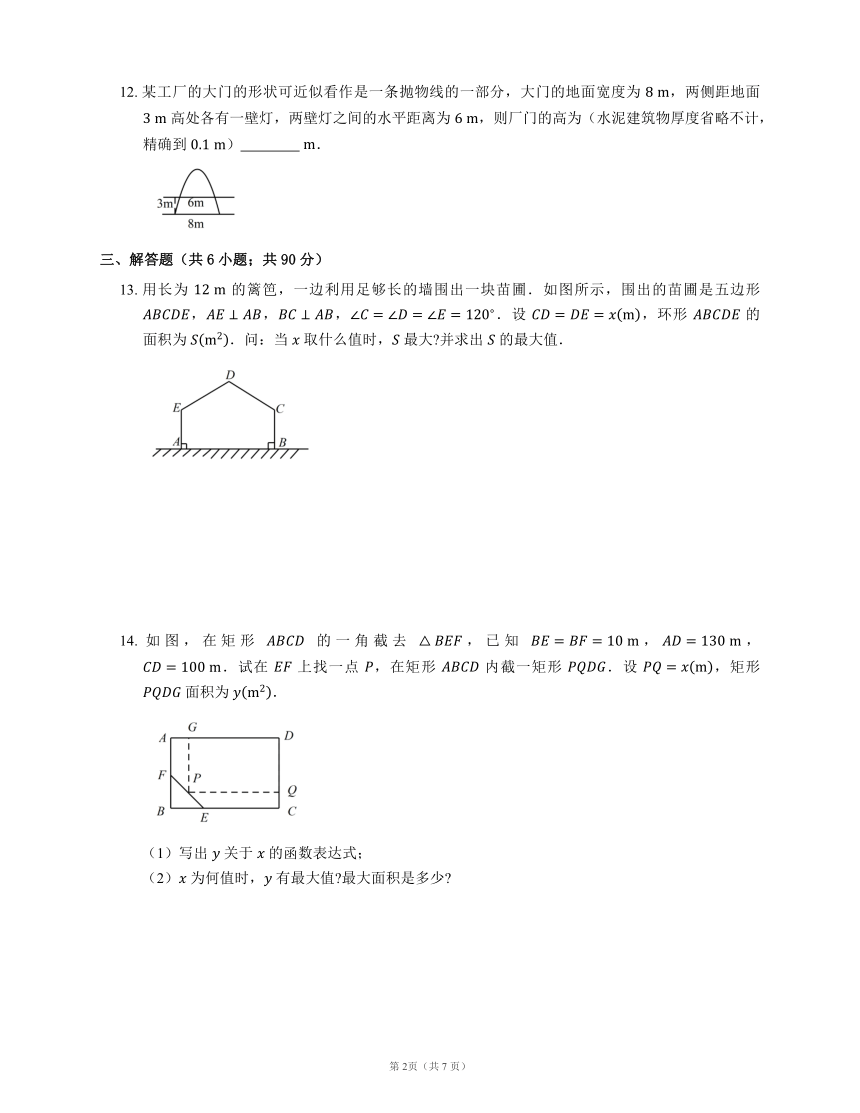
12.
某工厂的大门的形状可近似看作是一条抛物线的一部分,大门的地面宽度为
,两侧距地面
高处各有一壁灯,两壁灯之间的水平距离为
,则厂门的高为(水泥建筑物厚度省略不计,精确到
)
?
.
三、解答题(共6小题;共90分)
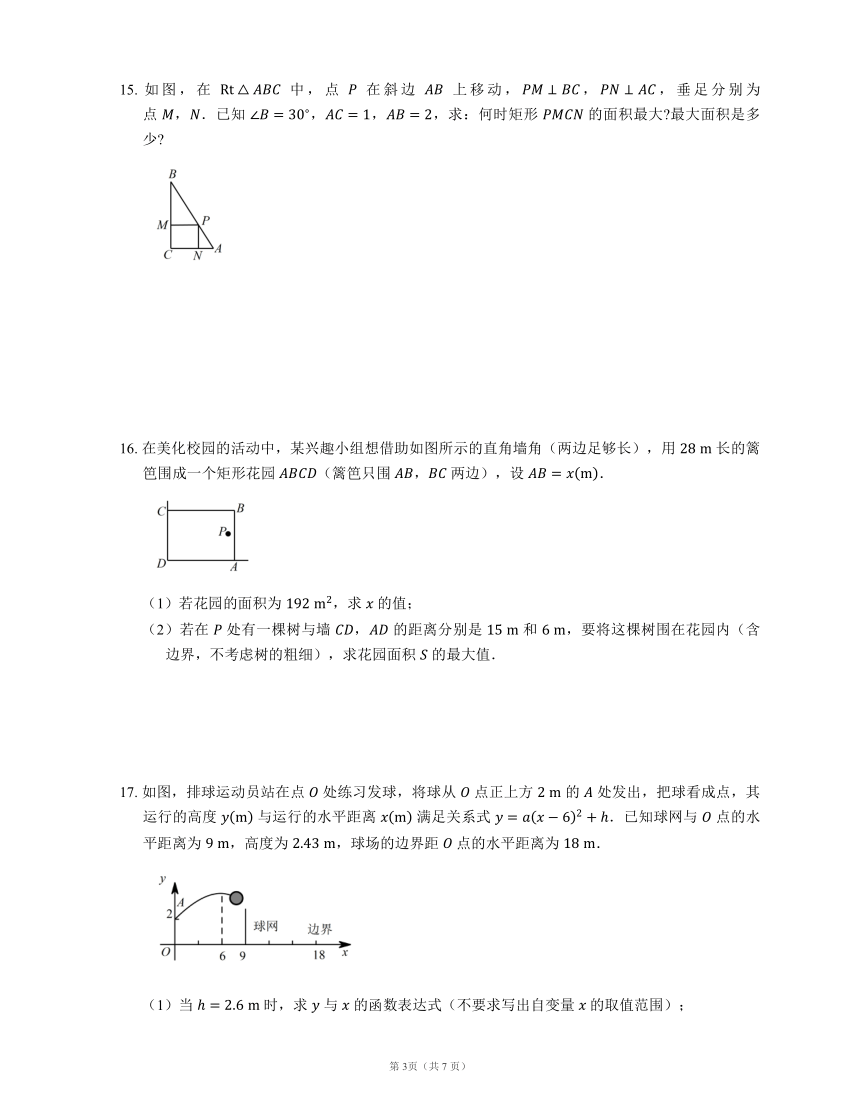
13.
用长为
的篱笆,一边利用足够长的墙围出一块苗圃.如图所示,围出的苗圃是五边形
,,,.设
,环形
的面积为
.问:当
取什么值时,
最大?并求出
的最大值.
14.
如图,在矩形
的一角截去
,已知
,,.试在
上找一点
,在矩形
内截一矩形
.设
,矩形
面积为
.
(1)写出
关于
的函数表达式;
(2)
为何值时,
有最大值?最大面积是多少?
15.
如图,在
中,点
在斜边
上移动,,,垂足分别为点
,.已知
,,,求:何时矩形
的面积最大?最大面积是多少?
16.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用
长的篱笆围成一个矩形花园
(篱笆只围
,
两边),设
.
(1)若花园的面积为
,求
的值;
(2)若在
处有一棵树与墙
,
的距离分别是
和
,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积
的最大值.
17.
如图,排球运动员站在点
处练习发球,将球从
点正上方
的
处发出,把球看成点,其运行的高度
与运行的水平距离
满足关系式
.已知球网与
点的水平距离为
,高度为
,球场的边界距
点的水平距离为
.
(1)当
时,求
与
的函数表达式(不要求写出自变量
的取值范围);
(2)当
时,球能否越过球网?球会不会出界?请说明理由(参考数据:).
18.
如图,有长为
的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度
).
(1)如果所围成的花圃的面积为
,试求宽
的长;
(2)按题目的设计要求,能围成面积比
更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
答案
第一部分
1.
C
2.
A
3.
A
4.
B
第二部分
5.
表达式,取值范围,配方变形,公式,最大值或最小值,自变量的取值范围
6.
,小,
7.
,
8.
9.
10.
,
11.
,
12.
第三部分
13.
连接
,过
作
,
,
,
又
,
,
,
设
,
在
中,,,
在
中,由三线合一得
为
中点,
,
,
当
时,,
当
取
时,
最大,
的最大值为
.
14.
(1)
延长
到
,则
.
在
中,,
,
,
.
??????(2)
,
当
时,
有最大值.
检验:,
不符题意,舍去.
在
时,
随
的增加而减小,
当
时,
有最大值,最大面积为
.
15.
设面积为
,,则以点
为坐标原点,
所在直线为
轴,
所在直线为
轴建立直角坐标系,则
,,,,
直线
的表达式为
,则点
的坐标为
.
.
矩形
的面积
,当
时,.
16.
(1)
,则
,
.
解得
,,
答:
的值为
或
.
??????(2)
,
,
,
在
处有一棵树与墙
,
的距离分别是
和
,,
,
当
时,
取得最大值为:.
答:花园面积
的最大值为
.
17.
(1)
,球从
点正上方
的
处发出,
过点
,
,解得:,
故
与
的表达式为
.
??????(2)
当
时,,
球能过球网;
当
时,,解得:,(舍去),
故会出界.
18.
(1)
设花圃的宽
米,知
应为
米,
故面积
与
的关系式为
.
当
时,,
解出
,.
当
时,,不合题意,舍去;
当
时,,符合题意.
故
长为
米.
??????(2)
能围成面积比
更大的矩形花圃.
由(1)知,.
墙体的最大可用长度
,
,
.
由抛物线
知,
在对称轴
的左侧,
随
的增大而增大,
当
时,
随
的增大而减小.
当
时,
最大值,
且最大值为
,
此时,,,
即围成长为
米,宽为
米的矩形
花圃时,
其最大面积为
.
第1页(共7
页)
二次函数的应用第1课时
利用二次函数解决面积最值问题
一、选择题(共4小题;共20分)
1.
用一根长为
的绳子围成一个矩形,其面积的最大值为
A.
B.
C.
D.
2.
如果二次函数
的最小值为负数,则
的取值范围是
A.
B.
C.
D.
3.
某广场有一喷水池,水从地面喷出,如图,以水平地面为
轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线
(单位:)的一部分,则水喷出的最大高度是
A.
B.
C.
D.
4.
向上发射一枚炮弹,经
后的高度为
,且时间与高度的关系为
,若此炮弹在第
秒与第
秒时的高度相等,则下列时间中,高度最高的是
A.
第
秒
B.
第
秒
C.
第
秒
D.
第
秒
二、填空题(共8小题;共40分)
5.
运用二次函数求实际问题中的最大值或最小值,首先应当求出函数
?
和自变量的
?,然后通过
?,或利用
?
求它的
?,取得最大值或最小值对应的自变量的值必须在
?
内.
6.
二次函数
,当
?
时,
有最
?
值,这个值是
?.
7.
设矩形窗户的周长为
,则窗户面积
与窗户宽
之间的函数表达式是
?,自变量
的取值范围是
?.
8.
正方形的边长为
,若边长增加
,那么面积增加
,则
关于
的函数表达式为
?.
9.
若两数的和为
,则这两个数的积最大可达到
?.
10.
函数
的最小值是
?,最大值是
?.
11.
如图,用
长的木条(厚度忽略不计),做一个有一条横档的矩形窗子框架,为使透进的光线最多,应选择窗子的长、宽各为
?
.
12.
某工厂的大门的形状可近似看作是一条抛物线的一部分,大门的地面宽度为
,两侧距地面
高处各有一壁灯,两壁灯之间的水平距离为
,则厂门的高为(水泥建筑物厚度省略不计,精确到
)
?
.
三、解答题(共6小题;共90分)
13.
用长为
的篱笆,一边利用足够长的墙围出一块苗圃.如图所示,围出的苗圃是五边形
,,,.设
,环形
的面积为
.问:当
取什么值时,
最大?并求出
的最大值.
14.
如图,在矩形
的一角截去
,已知
,,.试在
上找一点
,在矩形
内截一矩形
.设
,矩形
面积为
.
(1)写出
关于
的函数表达式;
(2)
为何值时,
有最大值?最大面积是多少?
15.
如图,在
中,点
在斜边
上移动,,,垂足分别为点
,.已知
,,,求:何时矩形
的面积最大?最大面积是多少?
16.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用
长的篱笆围成一个矩形花园
(篱笆只围
,
两边),设
.
(1)若花园的面积为
,求
的值;
(2)若在
处有一棵树与墙
,
的距离分别是
和
,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积
的最大值.
17.
如图,排球运动员站在点
处练习发球,将球从
点正上方
的
处发出,把球看成点,其运行的高度
与运行的水平距离
满足关系式
.已知球网与
点的水平距离为
,高度为
,球场的边界距
点的水平距离为
.
(1)当
时,求
与
的函数表达式(不要求写出自变量
的取值范围);
(2)当
时,球能否越过球网?球会不会出界?请说明理由(参考数据:).
18.
如图,有长为
的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度
).
(1)如果所围成的花圃的面积为
,试求宽
的长;
(2)按题目的设计要求,能围成面积比
更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
答案
第一部分
1.
C
2.
A
3.
A
4.
B
第二部分
5.
表达式,取值范围,配方变形,公式,最大值或最小值,自变量的取值范围
6.
,小,
7.
,
8.
9.
10.
,
11.
,
12.
第三部分
13.
连接
,过
作
,
,
,
又
,
,
,
设
,
在
中,,,
在
中,由三线合一得
为
中点,
,
,
当
时,,
当
取
时,
最大,
的最大值为
.
14.
(1)
延长
到
,则
.
在
中,,
,
,
.
??????(2)
,
当
时,
有最大值.
检验:,
不符题意,舍去.
在
时,
随
的增加而减小,
当
时,
有最大值,最大面积为
.
15.
设面积为
,,则以点
为坐标原点,
所在直线为
轴,
所在直线为
轴建立直角坐标系,则
,,,,
直线
的表达式为
,则点
的坐标为
.
.
矩形
的面积
,当
时,.
16.
(1)
,则
,
.
解得
,,
答:
的值为
或
.
??????(2)
,
,
,
在
处有一棵树与墙
,
的距离分别是
和
,,
,
当
时,
取得最大值为:.
答:花园面积
的最大值为
.
17.
(1)
,球从
点正上方
的
处发出,
过点
,
,解得:,
故
与
的表达式为
.
??????(2)
当
时,,
球能过球网;
当
时,,解得:,(舍去),
故会出界.
18.
(1)
设花圃的宽
米,知
应为
米,
故面积
与
的关系式为
.
当
时,,
解出
,.
当
时,,不合题意,舍去;
当
时,,符合题意.
故
长为
米.
??????(2)
能围成面积比
更大的矩形花圃.
由(1)知,.
墙体的最大可用长度
,
,
.
由抛物线
知,
在对称轴
的左侧,
随
的增大而增大,
当
时,
随
的增大而减小.
当
时,
最大值,
且最大值为
,
此时,,,
即围成长为
米,宽为
米的矩形
花圃时,
其最大面积为
.
第1页(共7
页)
同课章节目录
