2021-2022学年浙教版版九年级数学上册同步练习附答案:1.4 二次函数的应用第3课时 二次函数与一元二次方程
文档属性
| 名称 | 2021-2022学年浙教版版九年级数学上册同步练习附答案:1.4 二次函数的应用第3课时 二次函数与一元二次方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 10:27:11 | ||
图片预览



文档简介
1.4
二次函数的应用第3课时
二次函数与一元二次方程
一、选择题(共5小题;共25分)
1.
已知函数
的图象如图所示,那么关于
的方程
的根的情况是
A.
无实数根
B.
有两个相等的实数根
C.
有两个不相等的实数根
D.
无法确定
2.
二次函数
的图象如图所示,判断方程
的两根,下列叙述正确的是
A.
两根相异,且均为正根
B.
两根相异,且只有一个正根
C.
两根相同,且为正根
D.
两根相同,且为负根
3.
如图是小王用铁丝围成的面积为
的平行四边形
,其中
,.若他将此铁丝围成了一个矩形,则此矩形的面积不可能是
A.
B.
C.
D.
4.
现定义某种运算
,若
,那么
的取值范围是
A.
B.
或
C.
D.
5.
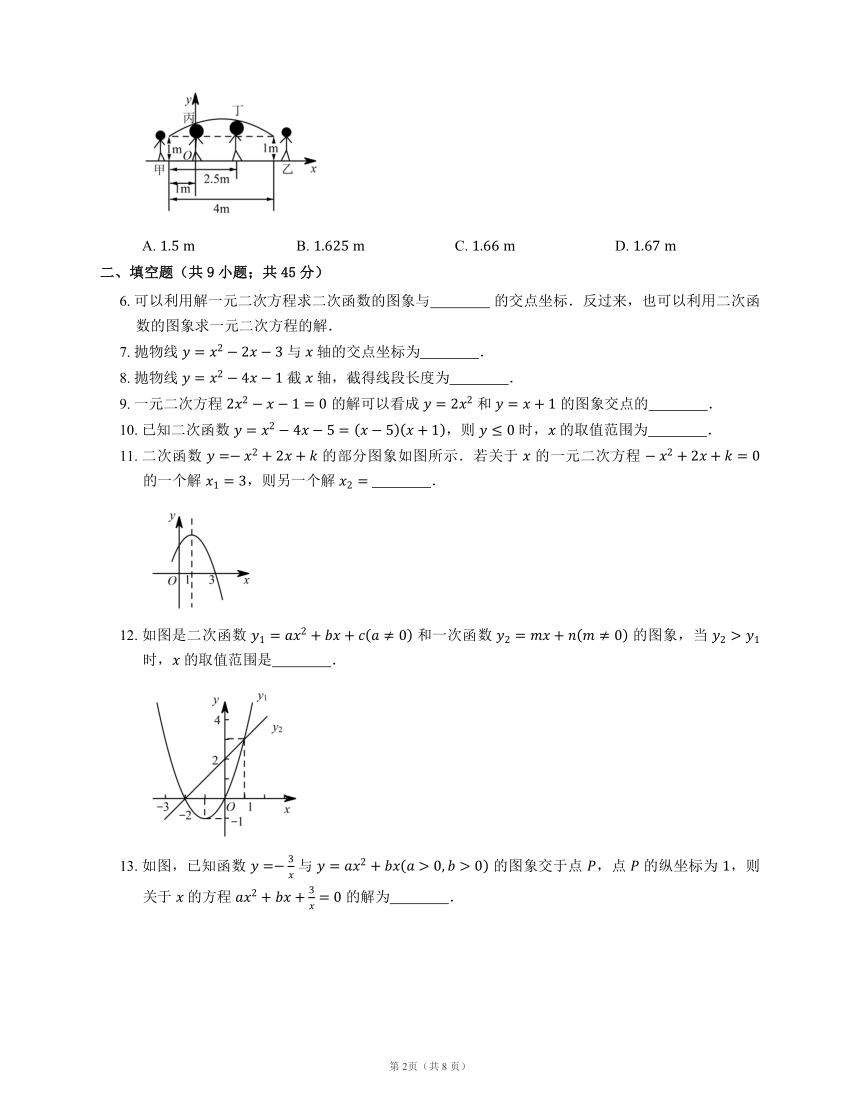
你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地看作抛物线,如图所示,建立直角坐标系,正在甩绳的甲、乙两名学生拿绳的手间距为
,距地面均为
,学生丙、丁分别站在距甲拿绳的手水平距离
,
处,绳子在甩到最高处时刚好通过他们的头顶,已知学生丙的身高是
,则学生丁的身高为
A.
B.
C.
D.
二、填空题(共9小题;共45分)
6.
可以利用解一元二次方程求二次函数的图象与
?
的交点坐标.反过来,也可以利用二次函数的图象求一元二次方程的解.
7.
抛物线
与
轴的交点坐标为
?.
8.
抛物线
截
轴,截得线段长度为
?.
9.
一元二次方程
的解可以看成
和
的图象交点的
?.
10.
已知二次函数
,则
时,
的取值范围为
?.
11.
二次函数
的部分图象如图所示.若关于
的一元二次方程
的一个解
,则另一个解
?.
12.
如图是二次函数
和一次函数
的图象,当
时,
的取值范围是
?.
13.
如图,已知函数
与
的图象交于点
,点
的纵坐标为
,则关于
的方程
的解为
?.
14.
若实数
,
满足
,则
的最小值是
?.
三、解答题(共5小题;共80分)
15.
如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点
落在水平面上,对称轴是水平线
.点
,
在抛物线造型上,且点
到水平面的距离
,点
到水平面距离为
,.
(1)请建立适当的直角坐标系,求抛物线的函数表达式;
(2)为了安全美观,现需在水平线
上找一点
,用质地、规格已确定的圆形钢管制作两根支柱
,
对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省时的点
(支柱与地面、造型对接方式的用料多少问题暂不考虑)?(无需证明)
(3)为了施工方便,现需计算出点
,
之间的距离,那么两根支柱用料最省时点
,
之间的距离是多少?
16.
下图是抛物线形拱桥的示意图,桥的跨度
为
,支撑桥的是一些等距的立柱,相邻立柱的水平距离为
,(不考虑立柱的粗细),其中距
点
处的立柱
的高度为
.
(1)求正中间的立柱
的高度;
(2)是否存在一根立柱,其高度恰好是
的一半?请说明理由.
17.
一名男生推铅球,铅球行进高度
(单位:)与水平距离
(单位:)之间的关系是
,铅球运行路线如图.
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到
米.
18.
如图,小明在一次高尔夫球争霸赛中,从山坡下
点打出一球向球洞
点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度
时,球移动的水平距离为
.已知山坡
与水平方向
的夹角为
,,
两点相距
.
(1)求出点
的坐标及直线
的函数表达式;
(2)求出球的飞行路线所在抛物线的函数表达式;
(3)判断小明这一杆能否把高尔夫球从
点直接打入球洞
点.
19.
(1)请在坐标系中画出二次函数
的大致图象;
(2)根据方程的根与函数图象的关系,将方程
的根在图上近似地表示出来(描点);
(3)观察图象,直接写出方程
的根.(精确到
)
答案
1.
B
2.
A
3.
D
4.
A
5.
B
6.
横轴(或平行于横轴的直线)
7.
和
8.
9.
横坐标
10.
11.
12.
13.
14.
【解析】,,
当
,
的值最小.
15.
(1)
以点
为原点、射线
为
轴的正半轴建立直角坐标系,设抛物线的函数表达式为
,由题意知点
的坐标为
.
点
在抛物线上,
,解得
,
所求抛物线的函数表达式为:.
??????(2)
延长
,交建筑物造型所在抛物线于点
,使点
,
关于
对称.
连接
交
于点
,则点
即为所求.
??????(3)
由题意知点
的横坐标为
,
点
在抛物线上,
点
的坐标为
,
又
点
的坐标为
,
点
的坐标为
,设直线
的函数表达式为
,
解得:,.
直线
的函数表达式为
,把
代入
,得点
的坐标为
,两根支柱用料最省时,点
,
之间的距离是
.
16.
(1)
根据题意可得中间立柱
经过
的中点
.以点
为原点,以射线
为
轴的正半轴,建立直角坐标系.问题转化为求点
的纵坐标.
,
故
,.设抛物线的表达式为
,
解得:
,
当
时,.即正中间的立柱
的高度是
;
??????(2)
不存在.设存在一根立柱的高度是
的一半,即这根立柱的高度是
.
则有
.
解得:.
相邻立柱之间的间距为
.最中间的立柱
在
轴上,根据题意每根立柱上的点的横坐标为
的整数倍,
.
与题意不符,
不存在一根立柱,其高度恰好是
高度的一半.
17.
(1)
当
时,,
解得
,(不合题意,舍去),
推铅球的水平距离是
.
??????(2)
当
时,
取最大值
,
铅球行进高度不能达到
,最高能达到
.
18.
(1)
在
中,
,,
,.
点
的坐标为
,设
的表达式为
,把点
的坐标代入得:,
,
的表达式为
.
??????(2)
顶点
的坐标是
,点
的坐标是
,
设抛物线的表达式为
,把点
的坐标代入得:,解得
,
抛物线的表达式为
,即
.
??????(3)
当
时,,
小明这一杆不能把高尔夫球从
点直接打入球洞
点.
19.
(1)
??????(2)
??????(3)
观察图象可得方程的根约为
,.
第1页(共8
页)
二次函数的应用第3课时
二次函数与一元二次方程
一、选择题(共5小题;共25分)
1.
已知函数
的图象如图所示,那么关于
的方程
的根的情况是
A.
无实数根
B.
有两个相等的实数根
C.
有两个不相等的实数根
D.
无法确定
2.
二次函数
的图象如图所示,判断方程
的两根,下列叙述正确的是
A.
两根相异,且均为正根
B.
两根相异,且只有一个正根
C.
两根相同,且为正根
D.
两根相同,且为负根
3.
如图是小王用铁丝围成的面积为
的平行四边形
,其中
,.若他将此铁丝围成了一个矩形,则此矩形的面积不可能是
A.
B.
C.
D.
4.
现定义某种运算
,若
,那么
的取值范围是
A.
B.
或
C.
D.
5.
你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地看作抛物线,如图所示,建立直角坐标系,正在甩绳的甲、乙两名学生拿绳的手间距为
,距地面均为
,学生丙、丁分别站在距甲拿绳的手水平距离
,
处,绳子在甩到最高处时刚好通过他们的头顶,已知学生丙的身高是
,则学生丁的身高为
A.
B.
C.
D.
二、填空题(共9小题;共45分)
6.
可以利用解一元二次方程求二次函数的图象与
?
的交点坐标.反过来,也可以利用二次函数的图象求一元二次方程的解.
7.
抛物线
与
轴的交点坐标为
?.
8.
抛物线
截
轴,截得线段长度为
?.
9.
一元二次方程
的解可以看成
和
的图象交点的
?.
10.
已知二次函数
,则
时,
的取值范围为
?.
11.
二次函数
的部分图象如图所示.若关于
的一元二次方程
的一个解
,则另一个解
?.
12.
如图是二次函数
和一次函数
的图象,当
时,
的取值范围是
?.
13.
如图,已知函数
与
的图象交于点
,点
的纵坐标为
,则关于
的方程
的解为
?.
14.
若实数
,
满足
,则
的最小值是
?.
三、解答题(共5小题;共80分)
15.
如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点
落在水平面上,对称轴是水平线
.点
,
在抛物线造型上,且点
到水平面的距离
,点
到水平面距离为
,.
(1)请建立适当的直角坐标系,求抛物线的函数表达式;
(2)为了安全美观,现需在水平线
上找一点
,用质地、规格已确定的圆形钢管制作两根支柱
,
对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省时的点
(支柱与地面、造型对接方式的用料多少问题暂不考虑)?(无需证明)
(3)为了施工方便,现需计算出点
,
之间的距离,那么两根支柱用料最省时点
,
之间的距离是多少?
16.
下图是抛物线形拱桥的示意图,桥的跨度
为
,支撑桥的是一些等距的立柱,相邻立柱的水平距离为
,(不考虑立柱的粗细),其中距
点
处的立柱
的高度为
.
(1)求正中间的立柱
的高度;
(2)是否存在一根立柱,其高度恰好是
的一半?请说明理由.
17.
一名男生推铅球,铅球行进高度
(单位:)与水平距离
(单位:)之间的关系是
,铅球运行路线如图.
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到
米.
18.
如图,小明在一次高尔夫球争霸赛中,从山坡下
点打出一球向球洞
点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度
时,球移动的水平距离为
.已知山坡
与水平方向
的夹角为
,,
两点相距
.
(1)求出点
的坐标及直线
的函数表达式;
(2)求出球的飞行路线所在抛物线的函数表达式;
(3)判断小明这一杆能否把高尔夫球从
点直接打入球洞
点.
19.
(1)请在坐标系中画出二次函数
的大致图象;
(2)根据方程的根与函数图象的关系,将方程
的根在图上近似地表示出来(描点);
(3)观察图象,直接写出方程
的根.(精确到
)
答案
1.
B
2.
A
3.
D
4.
A
5.
B
6.
横轴(或平行于横轴的直线)
7.
和
8.
9.
横坐标
10.
11.
12.
13.
14.
【解析】,,
当
,
的值最小.
15.
(1)
以点
为原点、射线
为
轴的正半轴建立直角坐标系,设抛物线的函数表达式为
,由题意知点
的坐标为
.
点
在抛物线上,
,解得
,
所求抛物线的函数表达式为:.
??????(2)
延长
,交建筑物造型所在抛物线于点
,使点
,
关于
对称.
连接
交
于点
,则点
即为所求.
??????(3)
由题意知点
的横坐标为
,
点
在抛物线上,
点
的坐标为
,
又
点
的坐标为
,
点
的坐标为
,设直线
的函数表达式为
,
解得:,.
直线
的函数表达式为
,把
代入
,得点
的坐标为
,两根支柱用料最省时,点
,
之间的距离是
.
16.
(1)
根据题意可得中间立柱
经过
的中点
.以点
为原点,以射线
为
轴的正半轴,建立直角坐标系.问题转化为求点
的纵坐标.
,
故
,.设抛物线的表达式为
,
解得:
,
当
时,.即正中间的立柱
的高度是
;
??????(2)
不存在.设存在一根立柱的高度是
的一半,即这根立柱的高度是
.
则有
.
解得:.
相邻立柱之间的间距为
.最中间的立柱
在
轴上,根据题意每根立柱上的点的横坐标为
的整数倍,
.
与题意不符,
不存在一根立柱,其高度恰好是
高度的一半.
17.
(1)
当
时,,
解得
,(不合题意,舍去),
推铅球的水平距离是
.
??????(2)
当
时,
取最大值
,
铅球行进高度不能达到
,最高能达到
.
18.
(1)
在
中,
,,
,.
点
的坐标为
,设
的表达式为
,把点
的坐标代入得:,
,
的表达式为
.
??????(2)
顶点
的坐标是
,点
的坐标是
,
设抛物线的表达式为
,把点
的坐标代入得:,解得
,
抛物线的表达式为
,即
.
??????(3)
当
时,,
小明这一杆不能把高尔夫球从
点直接打入球洞
点.
19.
(1)
??????(2)
??????(3)
观察图象可得方程的根约为
,.
第1页(共8
页)
同课章节目录
