九年级中考复习——等腰三角形

等腰三角形
中考热点1 等腰三角形的判定与性质
例1 已知：点O到△ABC的两边AB、AC所在的直线距离相等，且OB=OC
如图1，若点O在边BC上，求证：AB=AC
若图2，若点O在△ABC的内部，求证：AB=AC
若点O在△ABC的外部，AB=AC成立吗？请画图表示
【变形题组】 1、如图，在等腰△ABC中，CH是底边上的高，点P是线段CH上不与端点重合的任意一点，连接AP交BC于E，连接BP交AC于点F
（1）证明：∠CAE=∠CBF
（2）证明：AE=BF
（3）以线段AE，BF和AB为边构成一个新的△ABG（点E与点F重合于G点），记△ABC和△ABG的面积分别为和，如果存在点P，能使得，求∠C的取值范围
中考热点2 等边三角形的判定与性质
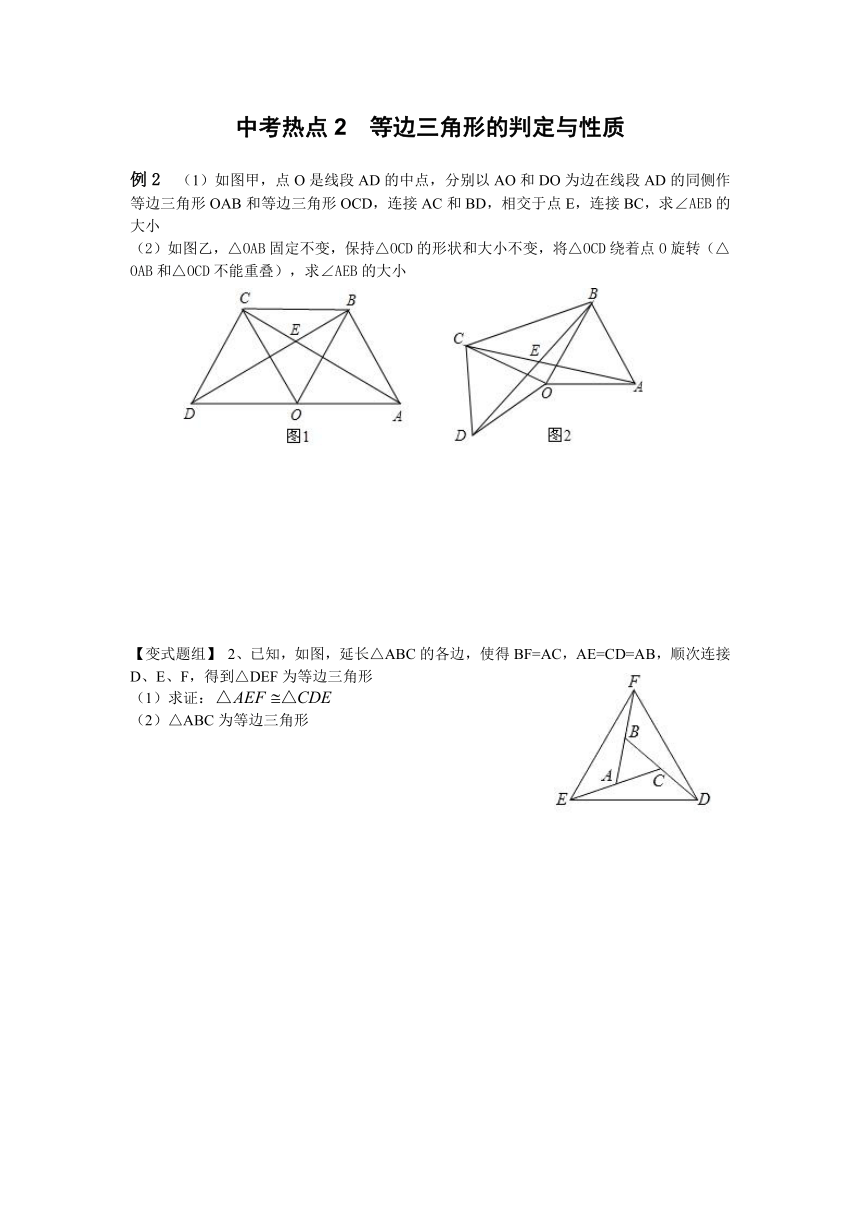
例2 （1）如图甲，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连接AC和BD，相交于点E，连接BC，求∠AEB的大小
（2）如图乙，△OAB固定不变，保持△OCD的形状和大小不变，将△OCD绕着点O旋转（△OAB和△OCD不能重叠），求∠AEB的大小
【变式题组】 2、已知，如图，延长△ABC的各边，使得BF=AC，AE=CD=AB，顺次连接D、E、F，得到△DEF为等边三角形
求证：
△ABC为等边三角形
操作与探究
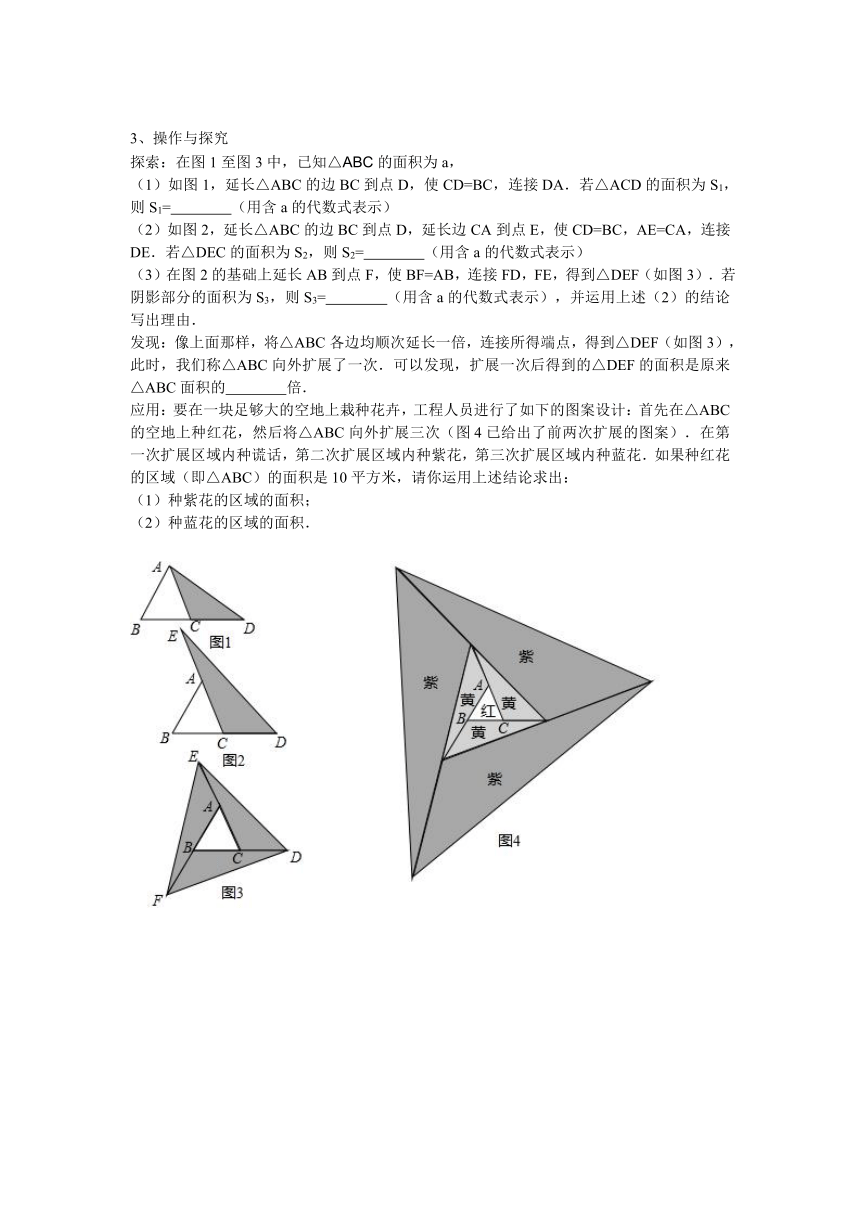
探索：在图1至图3中，已知△ABC的面积为a，
（1）如图1，延长△ABC的边BC到点D，使CD=BC，连接DA．若△ACD的面积为S1，则S1= （用含a的代数式表示）
（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连接DE．若△DEC的面积为S2，则S2= （用含a的代数式表示）
（3）在图2的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF（如图3）．若阴影部分的面积为S3，则S3= （用含a的代数式表示），并运用上述（2）的结论写出理由．
发现：像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF（如图3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的 倍．
应用：要在一块足够大的空地上栽种花卉，工程人员进行了如下的图案设计：首先在△ABC的空地上种红花，然后将△ABC向外扩展三次（图4已给出了前两次扩展的图案）．在第一次扩展区域内种谎话，第二次扩展区域内种紫花，第三次扩展区域内种蓝花．如果种红花的区域（即△ABC）的面积是10平方米，请你运用上述结论求出：
（1）种紫花的区域的面积；
（2）种蓝花的区域的面积．
中考热点3 线段垂直平分线的应用
例3 如图，已知AB=AC，∠A=36°，AB的中垂线MN交AC于点D，交AB于M，有下面四个结论：①射线BD是∠ABC的平分线；②△BCD是等腰三角形；③△ABC∽△BCD；④
判断其中正确的结论是那几个？
从你认为正确的结论中选出一个加以证明
【变式题组】4、如图，在△ABC中，BC=8cm，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长l=18cm，则AC的长等于 （ ）
A、6cm B、8cm C、10cm D、12cm
5、如图，AB=AC，∠BAC=120°，AB的垂直平分线交BC于D，那么∠ADC=
压轴题 函数图像中点的存在性问题——等腰三角形
例（2011 孝感）如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折叠边AD，使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m，0），其中m＞0．
（1）求点E、F的坐标（用含m的式子表示）；
（2）连接OA，若△OAF是等腰三角形，求m的值；
（3）如图（2），设抛物线经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求a、h、m的值．
作业3
已知等腰三角形的两边长分别为2和5，则它的周长为 （ ）
A、12或9 B、12 C、9 D、7
如图，△ABC中，AB=AC，∠A=30°，DE垂直平分AC，则∠BCD的度数为 （ ）
A、80° B、75° C、65° D、45°
3、如图所示，在钝角△ABC中，点D、E分别是AC、BC的中点，且DA=DE，那么下列结论错误的是 （ ）
A、∠1=∠2 B、∠1=∠3 C、∠B=∠C D、∠3=∠B
4、等腰三角形一腰上的高与腰长之比为1：2，则等腰三角形的顶角为
5、如图，△ABC和△DCE都是边长为2的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为
6、在一次数学课上，王老师在黑板上画出图，并写下了四个等式：①AB=DC，②BE=CE，③∠B=∠C，④∠BAE=∠CDE ；要求同学从这四个中选出两个作为条件，推出△AED为等腰三角形，请你试着完成王老师提出的要求，并说明理由（写出一种即可）
已知：
求证：△AED为等腰三角形
证明：