浙教版八下数学 4.2平行四边形 课件(共27张ppt)
文档属性
| 名称 | 浙教版八下数学 4.2平行四边形 课件(共27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-05 15:24:30 | ||
图片预览







文档简介
4.2 平行四边形
一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥了一块平行四边形的土地,由于年迈体弱,他决定把这块土地平均分给他的四个孩子,他的三个儿子想出了三种方案,都认为自己是对的,你说他们分得对吗?
老大
老二
老三
老四
老二
老大
老二
老三
老四
老大
老大
老二
老三
老四
老三
平行四边形用符号“ ”表示,例如: 平行四边形ABCD 可记做“ ”.
ABCD
两组对边分别平行的四边形
A
D
C
B
∠A与∠C,∠B与∠D
AB与CD,AD与BC
∠A与∠B,∠C与∠D等
AB与AD,AB与BC等
对边:
邻边:
对角:
邻角:
平行四边形定义的几何语言表达:
∵AB∥CD,AD∥BC
或∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
平行四边形的定义既是平行四边形的一种判定方法,同时又是它的性质。
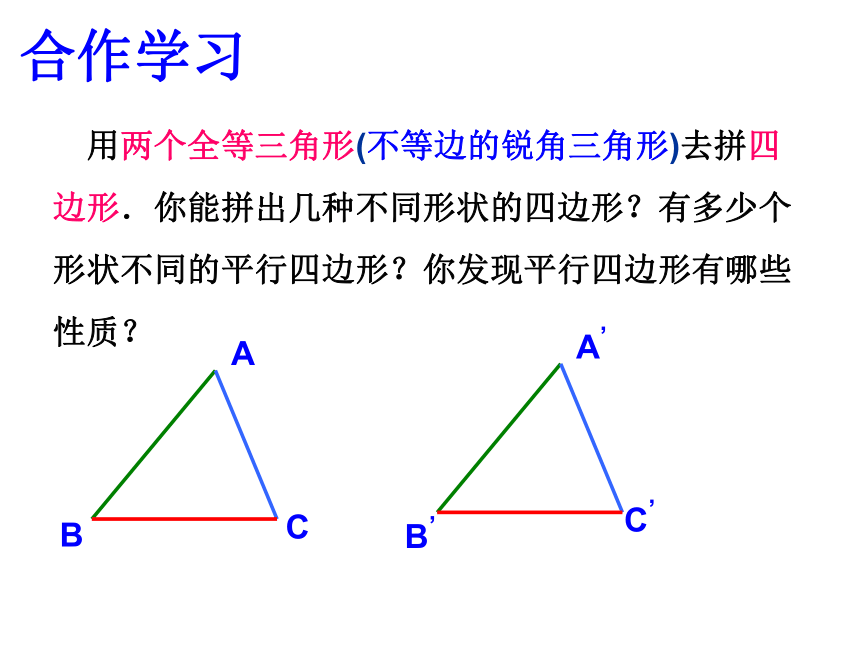
用两个全等三角形(不等边的锐角三角形)去拼四边形.你能拼出几种不同形状的四边形?有多少个形状不同的平行四边形?你发现平行四边形有哪些性质?
A
B
C
A,
B,
C,
合作学习
轴对称变换
?变换
轴对称图形
?图形
A
C
D
B
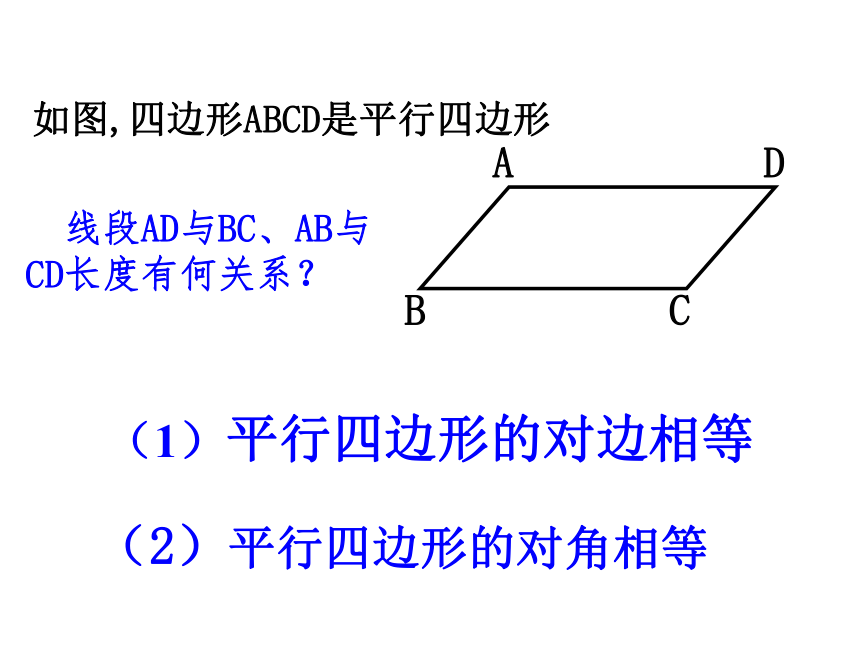
如图,四边形ABCD是平行四边形
线段AD与BC、AB与 CD长度有何关系?
(1)平行四边形的对边相等
(2)平行四边形的对角相等
证明命题:平行四边形的对边相等
已知:如图,四边形ABCD是平行四边形,
求证:AB=CD,AD=BC.
证明:连接AC.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,BC∥DA
∴ ∠1=∠2, ∠3=∠4.
∵ AC=CA,
∴ △ABC≌△CDA
∴ AB=CD,AD=BC.
(平行四边形的定义)
(两直线平行,内错角相等)
(ASA)
(全等三角形的对应边相等)
3
1
2
4
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
平行四边形的对角相等
平行四边形的对角相等,那么平行四边形的邻角又有怎样的关系呢?
已知:四边形ABCD是平行四边形。
求证:∠A+∠B=∠C+∠D=∠B+∠C=∠A+∠D=1800
证明:∵ 四边形ABCD是平行四边形
(平行四边形的定义)
∴ AB∥CD,AD∥BC
∴ ∠A+∠B=180°
∠C+∠B=180°
(两直线平行,同旁内角互补)
∠A+∠D=1800
∠C+∠D=1800
推论:平行四边形邻角互补
互补
1、如图,将□ABCD中边AB沿边BC作平移变换,
B
C
D
A
F
E
图中共有多少个平行四边形,并简单的说明理由。
3个
□ABCD
□ABEF
□FECD
练一练
2、已知 ABCD(如图),将它沿AB方向平移,平移的距离为 AB.
(1)作出经平移后所得的像;
(2)写出像与原平行四边形构成的图形中所有的
平行四边形。
练一练
例1 已知:如图,E,F分别是□ABCD
的边AD,BC上的点,且AF∥CE.
求证:DE=BF, ∠BAF=∠DCE
1.如图, ABCD中,AB∥ ,AD∥ .
2. ABCD中,∠A+∠D= ,∠A+∠B= ,
∠B+∠C= ,∠C+∠D= .
3.已知 ABCD中,∠A=55°,则∠B= ,∠C= ,
∠D= .
4.如图, ABCD中,∠BAC=26°,∠ACB=34°,
则∠ACD= ,∠D= .
CD
BC
180°
180°
180°
180°
125°
55°
125°
26°
120°
5.已知平行四边形的最大角比最小角大100o ,
求平行四边形的各个内角的度数.
x+(100o+x)=180o
x=40o
平行四边形的各个内角的度数为:40o,140o,40o,140o
解:设最小角为x,则最大角为100o+x。
6、 ABCD的四个角的度数的比∠A :∠B :∠C :∠D 可能是( )
2:5:2:5 B. 3:4:4:3
C. 4:4:2:2 D. 2:3:4:5
A
与三角形的稳定性相反,四边形具有不稳定性
练一练
1、如图:在 ABCD中,AE⊥DC
于E,AF⊥BC于F,∠EAF=650,
求 ABCD各个内角的度数。
2、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵
树应该栽在哪里?
谈谈这节课的收获
1、平行四边形的定义:两组对边分别平行的四边形。
3、平行四边形的对角相等。
4、平行四边形的不稳定性在实际生活中的应用。
2、平行四边形的对边相等。
1、如图,M是 ABCD边AD上任一点,若△CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S,S1,S2之间有什么样的关系,并说明理由.
拓展与延伸
N
方案设计:若你手中只有卷尺这一样工具,你能设计一个满足上述条件的方案吗,使得道路AECF的两条边AF、CE分别平分□ ABCD的两个对角?
2、一块平行四边形ABCD场地中,道路AECF的两条边AF、CE分别平分□ ABCD的两个对角,这条道路形状是平行四边形吗?请证明你的判断。
E
F
D
A
B
C
拓展与延伸
3、有一种汽车用“千斤顶”,它由4根连杆组成菱形ABCD,当螺旋装置顺时针旋转时,B、D两点的距离变小,从而顶起汽车。若AB=30,螺旋装置每顺时针旋转1圈,BD的长就减少1。设BD=a,AC=h,
(1)当a=40时,求h的值;
(2)从a=40开始,设螺旋装置顺时针方
向旋转x圈,求h关于x的函数解析式;
(3)从a=40开始,螺旋装置顺时针
方向连续旋转2圈,设第1圈使“千
斤顶”增高s1,第2圈使“千斤顶”
增高s2,试判定s1与s2的大小,并
说明理由了;若将条件“从a=40开始”改为“从某一时刻开始”,则结果如何?为什么?
拓展与延伸
一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥了一块平行四边形的土地,由于年迈体弱,他决定把这块土地平均分给他的四个孩子,他的三个儿子想出了三种方案,都认为自己是对的,你说他们分得对吗?
老大
老二
老三
老四
老二
老大
老二
老三
老四
老大
老大
老二
老三
老四
老三
平行四边形用符号“ ”表示,例如: 平行四边形ABCD 可记做“ ”.
ABCD
两组对边分别平行的四边形
A
D
C
B
∠A与∠C,∠B与∠D
AB与CD,AD与BC
∠A与∠B,∠C与∠D等
AB与AD,AB与BC等
对边:
邻边:
对角:
邻角:
平行四边形定义的几何语言表达:
∵AB∥CD,AD∥BC
或∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
平行四边形的定义既是平行四边形的一种判定方法,同时又是它的性质。
用两个全等三角形(不等边的锐角三角形)去拼四边形.你能拼出几种不同形状的四边形?有多少个形状不同的平行四边形?你发现平行四边形有哪些性质?
A
B
C
A,
B,
C,
合作学习
轴对称变换
?变换
轴对称图形
?图形
A
C
D
B
如图,四边形ABCD是平行四边形
线段AD与BC、AB与 CD长度有何关系?
(1)平行四边形的对边相等
(2)平行四边形的对角相等
证明命题:平行四边形的对边相等
已知:如图,四边形ABCD是平行四边形,
求证:AB=CD,AD=BC.
证明:连接AC.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,BC∥DA
∴ ∠1=∠2, ∠3=∠4.
∵ AC=CA,
∴ △ABC≌△CDA
∴ AB=CD,AD=BC.
(平行四边形的定义)
(两直线平行,内错角相等)
(ASA)
(全等三角形的对应边相等)
3
1
2
4
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
平行四边形的对角相等
平行四边形的对角相等,那么平行四边形的邻角又有怎样的关系呢?
已知:四边形ABCD是平行四边形。
求证:∠A+∠B=∠C+∠D=∠B+∠C=∠A+∠D=1800
证明:∵ 四边形ABCD是平行四边形
(平行四边形的定义)
∴ AB∥CD,AD∥BC
∴ ∠A+∠B=180°
∠C+∠B=180°
(两直线平行,同旁内角互补)
∠A+∠D=1800
∠C+∠D=1800
推论:平行四边形邻角互补
互补
1、如图,将□ABCD中边AB沿边BC作平移变换,
B
C
D
A
F
E
图中共有多少个平行四边形,并简单的说明理由。
3个
□ABCD
□ABEF
□FECD
练一练
2、已知 ABCD(如图),将它沿AB方向平移,平移的距离为 AB.
(1)作出经平移后所得的像;
(2)写出像与原平行四边形构成的图形中所有的
平行四边形。
练一练
例1 已知:如图,E,F分别是□ABCD
的边AD,BC上的点,且AF∥CE.
求证:DE=BF, ∠BAF=∠DCE
1.如图, ABCD中,AB∥ ,AD∥ .
2. ABCD中,∠A+∠D= ,∠A+∠B= ,
∠B+∠C= ,∠C+∠D= .
3.已知 ABCD中,∠A=55°,则∠B= ,∠C= ,
∠D= .
4.如图, ABCD中,∠BAC=26°,∠ACB=34°,
则∠ACD= ,∠D= .
CD
BC
180°
180°
180°
180°
125°
55°
125°
26°
120°
5.已知平行四边形的最大角比最小角大100o ,
求平行四边形的各个内角的度数.
x+(100o+x)=180o
x=40o
平行四边形的各个内角的度数为:40o,140o,40o,140o
解:设最小角为x,则最大角为100o+x。
6、 ABCD的四个角的度数的比∠A :∠B :∠C :∠D 可能是( )
2:5:2:5 B. 3:4:4:3
C. 4:4:2:2 D. 2:3:4:5
A
与三角形的稳定性相反,四边形具有不稳定性
练一练
1、如图:在 ABCD中,AE⊥DC
于E,AF⊥BC于F,∠EAF=650,
求 ABCD各个内角的度数。
2、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵
树应该栽在哪里?
谈谈这节课的收获
1、平行四边形的定义:两组对边分别平行的四边形。
3、平行四边形的对角相等。
4、平行四边形的不稳定性在实际生活中的应用。
2、平行四边形的对边相等。
1、如图,M是 ABCD边AD上任一点,若△CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S,S1,S2之间有什么样的关系,并说明理由.
拓展与延伸
N
方案设计:若你手中只有卷尺这一样工具,你能设计一个满足上述条件的方案吗,使得道路AECF的两条边AF、CE分别平分□ ABCD的两个对角?
2、一块平行四边形ABCD场地中,道路AECF的两条边AF、CE分别平分□ ABCD的两个对角,这条道路形状是平行四边形吗?请证明你的判断。
E
F
D
A
B
C
拓展与延伸
3、有一种汽车用“千斤顶”,它由4根连杆组成菱形ABCD,当螺旋装置顺时针旋转时,B、D两点的距离变小,从而顶起汽车。若AB=30,螺旋装置每顺时针旋转1圈,BD的长就减少1。设BD=a,AC=h,
(1)当a=40时,求h的值;
(2)从a=40开始,设螺旋装置顺时针方
向旋转x圈,求h关于x的函数解析式;
(3)从a=40开始,螺旋装置顺时针
方向连续旋转2圈,设第1圈使“千
斤顶”增高s1,第2圈使“千斤顶”
增高s2,试判定s1与s2的大小,并
说明理由了;若将条件“从a=40开始”改为“从某一时刻开始”,则结果如何?为什么?
拓展与延伸
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
