1.4 二次函数的应用 同步练习(含答案)
文档属性
| 名称 | 1.4 二次函数的应用 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 363.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 15:55:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.4
二次函数的应用
一、单选题
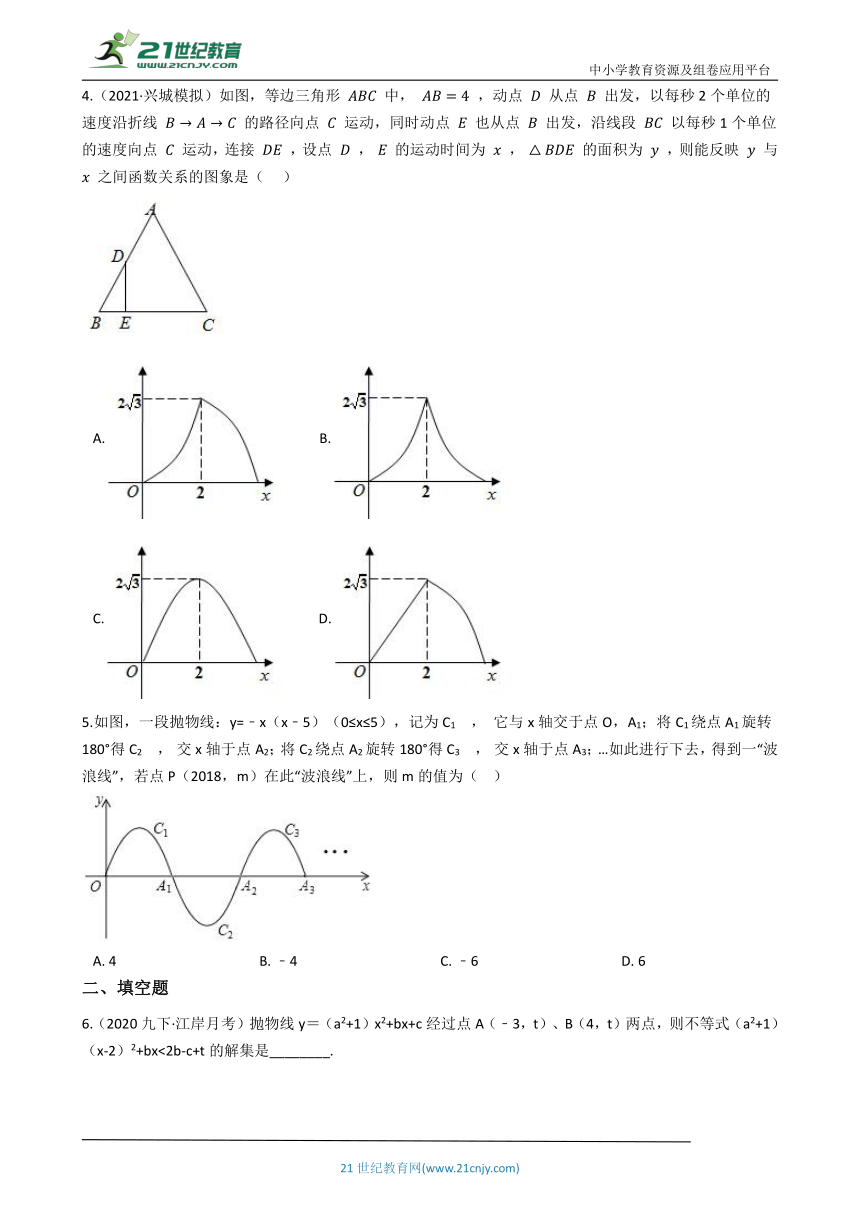
1.(2018九上·温州开学考)如图,抛物线
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为(??
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
2.(2020·台州模拟)在平面直角坐标系内,已知点A(﹣1,0),点B(1,1)都在直线y=
x+
上,若抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( )
A.?a≤﹣2???????????????????????B.?a<
???????????????????????C.?1≤a<
或a≤﹣2???????????????????????D.?﹣2≤a<
3.(2019九下·河南月考)如图,抛物线
与x轴交于点A、B,把抛物线在x轴及其下方的部分记作
,将
向左平移得到
,
与x轴交于点B、D,若直线
与
、
共有3个不同的交点,则m的取值范围是(??
)
A.?????????B.?????????C.?????????D.?
4.(2021·兴城模拟)如图,等边三角形
中,
,动点
从点
出发,以每秒2个单位的速度沿折线
的路径向点
运动,同时动点
也从点
出发,沿线段
以每秒1个单位的速度向点
运动,连接
,设点
,
的运动时间为
,
的面积为
,则能反映
与
之间函数关系的图象是(???
)
A.?
B.?
C.?
D.?
5.如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1
,
它与x轴交于点O,A1;将C1绕点A1旋转180°得C2
,
交x轴于点A2;将C2绕点A2旋转180°得C3
,
交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为(?
?)
A.?4?????????????????????????????????????????B.?﹣4?????????????????????????????????????????C.?﹣6?????????????????????????????????????????D.?6
二、填空题
6.(2020九下·江岸月考)抛物线y=(a2+1)x2+bx+c经过点A(﹣3,t)、B(4,t)两点,则不等式(a2+1)(x-2)2+bx<2b-c+t的解集是________.
7.(2019九下·衡水期中)如果直线y=kx+b与抛物线y=
x2交于A(x1
,
y1),B(x2
,
y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为________.[提示:直线l1:y=k1x+b1与直线l2:y=k2x+b2互相垂直,则k1?k2=-1]
8.(2017·武汉模拟)定义函数f(x),当x≤3时,f(x)=x2﹣2x,当x>3时,f(x)=x2﹣10x+24,若方程f(x)=2x+m有且只有两个实数解,则m的取值范围为________.
9.(2018·通城模拟)不等式x2+ax+b≥0(a≠0)的解集为全体实数,假设f(x)=x2+ax+b,若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为________
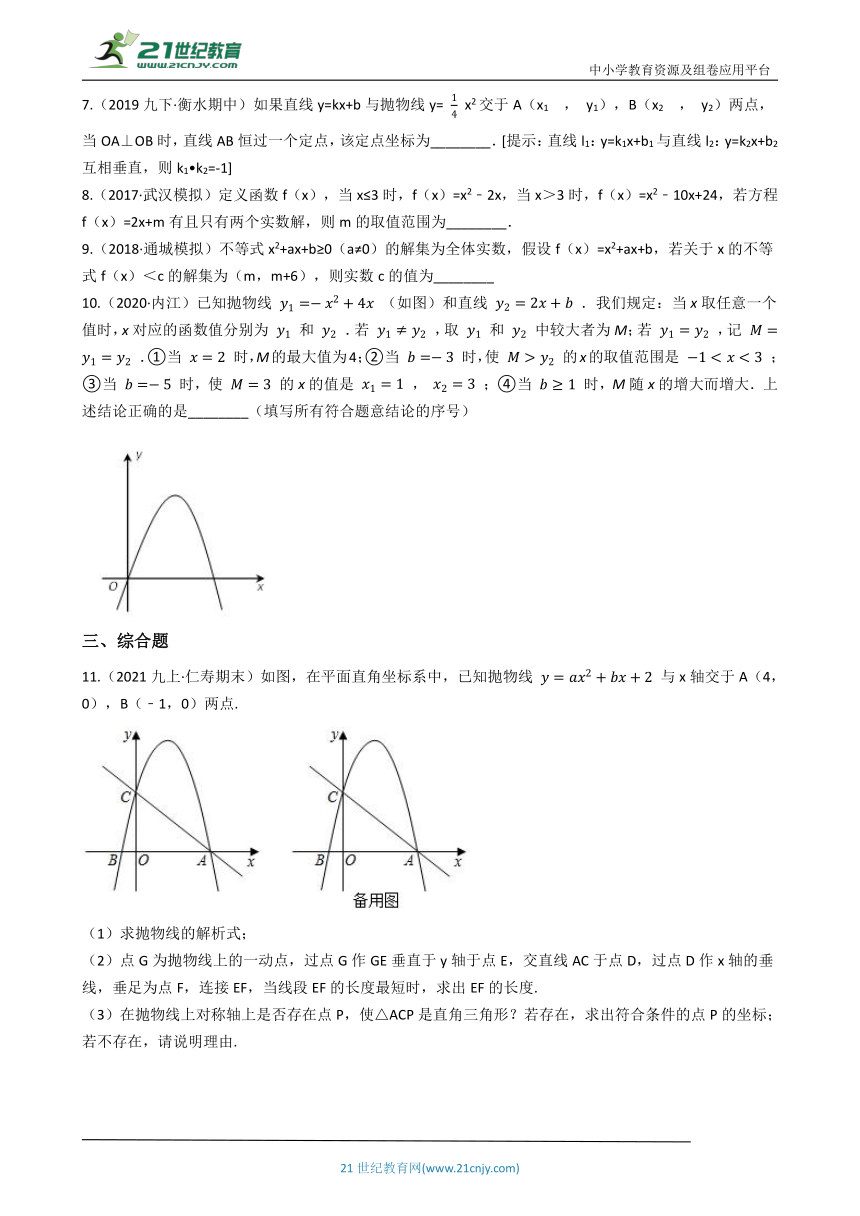
10.(2020·内江)已知抛物线
(如图)和直线
.我们规定:当x取任意一个值时,x对应的函数值分别为
和
.若
,取
和
中较大者为M;若
,记
.①当
时,M的最大值为4;②当
时,使
的x的取值范围是
;③当
时,使
的x的值是
,
;④当
时,M随x的增大而增大.上述结论正确的是________(填写所有符合题意结论的序号)
三、综合题
11.(2021九上·仁寿期末)如图,在平面直角坐标系中,已知抛物线
与x轴交于A(4,0),B(﹣1,0)两点.
(1)求抛物线的解析式;
(2)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出EF的长度.
(3)在抛物线上对称轴上是否存在点P,使△ACP是直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
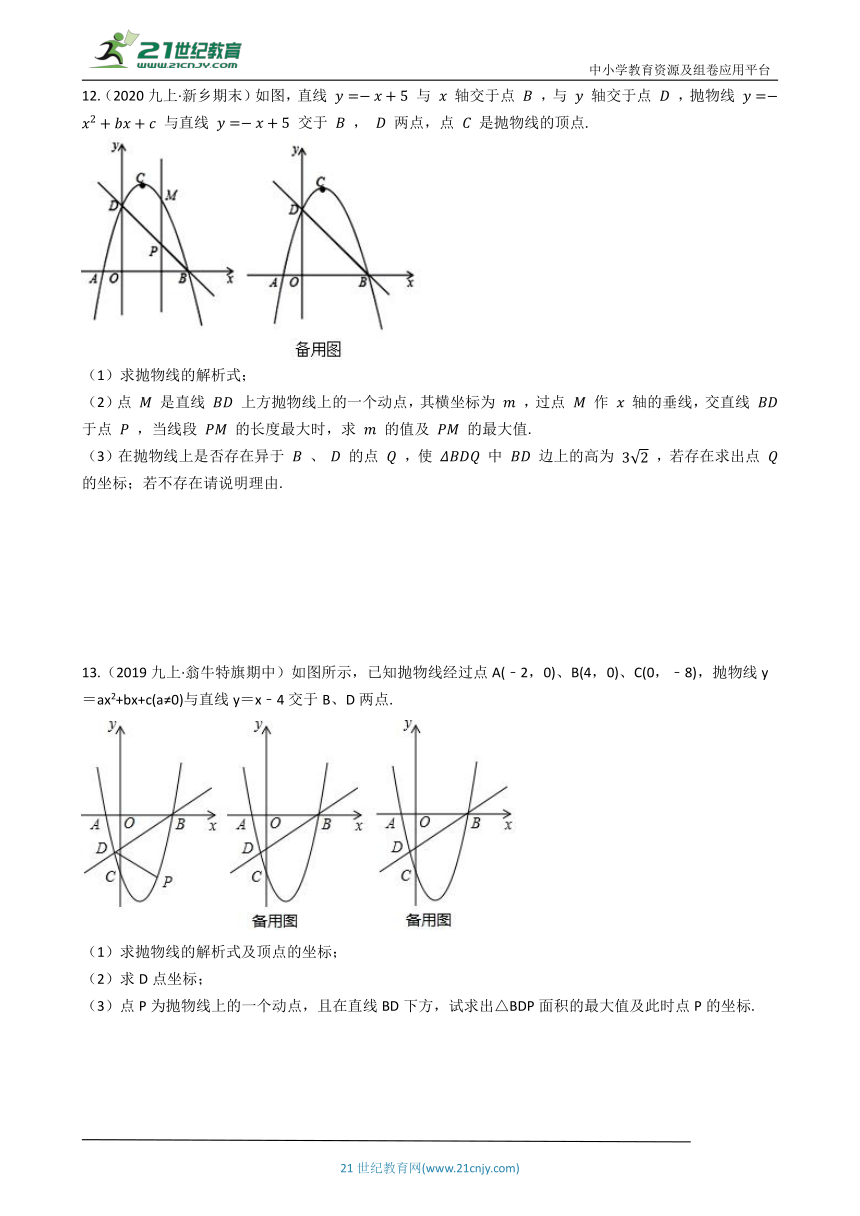
12.(2020九上·新乡期末)如图,直线
与
轴交于点
,与
轴交于点
,抛物线
与直线
交于
,
两点,点
是抛物线的顶点.
(1)求抛物线的解析式;
(2)点
是直线
上方抛物线上的一个动点,其横坐标为
,过点
作
轴的垂线,交直线
于点
,当线段
的长度最大时,求
的值及
的最大值.
(3)在抛物线上是否存在异于
、
的点
,使
中
边上的高为
,若存在求出点
的坐标;若不存在请说明理由.
13.(2019九上·翁牛特旗期中)如图所示,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8),抛物线y=ax2+bx+c(a≠0)与直线y=x﹣4交于B、D两点.
(1)求抛物线的解析式及顶点的坐标;
(2)求D点坐标;
(3)点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标.
14.(2019八下·绿园期末)已知,如图,正方形
的边长为4厘米,点
从点
出发,经
沿正方形的边以2厘米/秒的速度运动;同时,点
从点
出发以1厘米/秒的速度沿
向点
运动,设运动时间为t秒,
的面积为
平方厘米.
(1)当
时,
的面积为________平方厘米;
(2)求
的长(用含
的代数式表示);
(3)当点
在线段
上运动,且
为等腰三角形时,求此时
的值;
(4)求
与
之间的函数关系式.
15.(2019九上·西安月考)在平面直角坐标系中,二次函数
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
C
3.【答案】
C
4.【答案】
A
5.【答案】
C
二、填空题
6.【答案】
-1<x<6
7.【答案】
(0,4)
8.【答案】
m>﹣3或﹣12<m<﹣4
9.【答案】
9
10.【答案】
②③④
三、综合题
11.【答案】
(1)解:∵抛物线y=ax2+bx+2经过点A(4,0),B(﹣1,0),
∴
,
解得:
,
∴抛物线的解析式为:y=
x2+
x+2;
(2)解:连接OD,由题意知,四边形OFDE是矩形,则OD=EF,据垂线段最短,可知:
?
当OD⊥AC时,OD最短,即EF最短.
由(1)知,在Rt△AOC中,OC=2,OA=4,
∴AC=
.
∵
,
∴
,
故EF的长度为
;
(3)解:假设存在,设点P的坐标为(m,
m2+
m+2).
∵点A的坐标为(4,0),点C的坐标为(0,2),
∴AP2=(m﹣4)2+(
m2+
m+2﹣0)2
,
CP2=(m﹣0)2+(
m2+
m+2﹣2)2
,
AC2=(0﹣4)2+(2﹣0)2=20.
分两种情况考虑,①当∠ACP=90°时,AP2=CP2+AC2
,
即(m﹣4)2+(
m2+
m+2﹣0)2=(m﹣0)2+(
m2+
m+2﹣2)2+20,
解得:m1=0(舍去),m2=-1,
∴点P的坐标为(-1,0);
②当∠APC=90°时,CP2+AP2=AC2
,
即,(m﹣4)2+(
m2+
m+2﹣0)2+(m﹣0)2+(
m2+
m+2﹣2)2=20
解得:m1=0(舍去),m2=4(舍去),m3=m4=1,
∴点P的坐标为(1,3).
综上所述,假设成立,
即存在点P(-1,0)或(1,3),使得△ACP是直角三角形.
12.【答案】
(1)解:
,令
,则
,令
,则
,
故点
、
的坐标分别为
、
,
将
、
代入二次函数表达式为
,
解得:
,
故抛物线的表达式为:
.
(2)解:设
点横坐标为
,则
,
,
,
当
时,PM有最大值
(3)解:如图,过
作
轴交
于点
,交
轴于点
,作
于
,
设
,则
,
,
是等腰直角三角形,
,
,
当
中
边上的高为
时,即
,
,
,
当
时,解得
或
,
或
,
当
时,解得
或
,
或
,
综上可知存在满足条件的点
,其坐标为
,
,
,
.
13.【答案】
(1)解:抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
故﹣8a=﹣8,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣8;
∴
,故顶点坐标为(1,-9)
(2)解:抛物线与直线交于BD两点,
依题意得:
,
解得:
,
,
故点D(﹣1,﹣5);
(3)解:过点P作y轴的平行线交BD于点H,
设点P(x,x2﹣2x﹣8),则点H(x,x﹣4)
△BDP面积=
PH×(xB﹣xD)=
×(x﹣4﹣x2+2x+8)×(4+1)=
,
∵
0,故面积有最大值为:
;
此时,x=
,P点纵坐标为
,
即点P(
,
).
14.【答案】
(1)8
(2)解:分两种情况:
当0≤t≤2时,P在AB上,BP=AB﹣AP=4﹣2t,当2<t≤4时,P在BC上,BP=2t﹣4;
综上所述:BP=
;
(3)解:如图2.
∵△PCQ为等腰三角形,∴CQ=CP,即t=8﹣2t,t
,∴当点P在线段BC上运动,且△PCQ为等腰三角形时,此时t的值是
秒;
(4)解:分两种情况:
①当0≤t≤2时,P在AB上,如图3.
S
4t
②当2<t≤4时,P在BC上,如图4.
S=S正方形ABCD﹣S△ABP﹣S△CPQ﹣S△ADQ=4×4
t2﹣6t+16;
综上所述:S与t之间的函数关系式为:S
.
15.【答案】
(1)由抛物线
过A(-3,0),B(1,0),则
,解得
.
∴二次函数的关系解析式为
.
(2)设点P坐标为(m,n),则
.
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
PM
=
,
,AO=3.
当
时,
,所以OC=2.
∵
<0,∴函数
有最大值,当
时,
有最大值.
此时
.
∴存在点
,使△ACP的面积最大.
(3)如图(3)所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3,则点Q1,Q2,Q3,Q4为符合题意要求的点.
过Q1点作Q1D⊥y轴于点D,
∵∠BCQ1=90°,
∴∠Q1CD+∠OCB=90°,
又∵在直角△OBC中,∠OCB+∠CBO=90°,
∴∠Q1CD=∠OCB,
又∵Q1C=BC,∠Q1DC=∠BOC,
∴△Q1CD≌△CBO,
∴Q1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q1(2,3);
同理求得Q2(3,1),Q3(?1,?1),Q4(?2,1).
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(?1,?1),Q4(?2,1).
(4)如图(4)所示,设E(n,0),则BE=1?n,
.
假设以点B.?Q、E为顶点的三角形与△AOC相似,则有两种情况:
①若△AOC∽△BEQ,则有:
,
即
,化简得:n2+n?2=0,
解得n1=?2,n2=1(与B重合,舍去),
∴n=?2,
.
∴Q(?2,2);
②若△AOC∽△BQE,则有:
,
即
,化简得:4n2?n?3=0,
解得
(与B重合,舍去),
∴
.
综上所述,存在点Q,使以点B.?Q、E为顶点的三角形与△AOC相似.
Q点坐标为(?2,2)或
.
(5)假设存在点Q,使以A.
C.?M、Q为顶点的四边形是平行四边形.
①若CM平行于x轴,如图(5)a所示,有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.
∵CM∥x轴,∴点M、点C(0,2)关于对称轴x=?1对称,
∴M(?2,2),
∴CM=2.
由Q1A=Q2A=CM=2,得到Q1(?5,0),Q2(?1,0);
②若CM不平行于x轴,如图(5)b所示.过点M作MG⊥x轴于G,
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=?2.
设M(x,?2),则有
,
解得
又QG=3,
∴
,
综上所述,存在点Q,使以A.
C.?M、Q为顶点的四边形是平行四边形.Q点坐标为:
.
21世纪教育网(www.21cnjy.com)
1.4
二次函数的应用
一、单选题
1.(2018九上·温州开学考)如图,抛物线
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为(??
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
2.(2020·台州模拟)在平面直角坐标系内,已知点A(﹣1,0),点B(1,1)都在直线y=
x+
上,若抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( )
A.?a≤﹣2???????????????????????B.?a<
???????????????????????C.?1≤a<
或a≤﹣2???????????????????????D.?﹣2≤a<
3.(2019九下·河南月考)如图,抛物线
与x轴交于点A、B,把抛物线在x轴及其下方的部分记作
,将
向左平移得到
,
与x轴交于点B、D,若直线
与
、
共有3个不同的交点,则m的取值范围是(??
)
A.?????????B.?????????C.?????????D.?
4.(2021·兴城模拟)如图,等边三角形
中,
,动点
从点
出发,以每秒2个单位的速度沿折线
的路径向点
运动,同时动点
也从点
出发,沿线段
以每秒1个单位的速度向点
运动,连接
,设点
,
的运动时间为
,
的面积为
,则能反映
与
之间函数关系的图象是(???
)
A.?
B.?
C.?
D.?
5.如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1
,
它与x轴交于点O,A1;将C1绕点A1旋转180°得C2
,
交x轴于点A2;将C2绕点A2旋转180°得C3
,
交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为(?
?)
A.?4?????????????????????????????????????????B.?﹣4?????????????????????????????????????????C.?﹣6?????????????????????????????????????????D.?6
二、填空题
6.(2020九下·江岸月考)抛物线y=(a2+1)x2+bx+c经过点A(﹣3,t)、B(4,t)两点,则不等式(a2+1)(x-2)2+bx<2b-c+t的解集是________.
7.(2019九下·衡水期中)如果直线y=kx+b与抛物线y=
x2交于A(x1
,
y1),B(x2
,
y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为________.[提示:直线l1:y=k1x+b1与直线l2:y=k2x+b2互相垂直,则k1?k2=-1]
8.(2017·武汉模拟)定义函数f(x),当x≤3时,f(x)=x2﹣2x,当x>3时,f(x)=x2﹣10x+24,若方程f(x)=2x+m有且只有两个实数解,则m的取值范围为________.
9.(2018·通城模拟)不等式x2+ax+b≥0(a≠0)的解集为全体实数,假设f(x)=x2+ax+b,若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为________
10.(2020·内江)已知抛物线
(如图)和直线
.我们规定:当x取任意一个值时,x对应的函数值分别为
和
.若
,取
和
中较大者为M;若
,记
.①当
时,M的最大值为4;②当
时,使
的x的取值范围是
;③当
时,使
的x的值是
,
;④当
时,M随x的增大而增大.上述结论正确的是________(填写所有符合题意结论的序号)
三、综合题
11.(2021九上·仁寿期末)如图,在平面直角坐标系中,已知抛物线
与x轴交于A(4,0),B(﹣1,0)两点.
(1)求抛物线的解析式;
(2)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出EF的长度.
(3)在抛物线上对称轴上是否存在点P,使△ACP是直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
12.(2020九上·新乡期末)如图,直线
与
轴交于点
,与
轴交于点
,抛物线
与直线
交于
,
两点,点
是抛物线的顶点.
(1)求抛物线的解析式;
(2)点
是直线
上方抛物线上的一个动点,其横坐标为
,过点
作
轴的垂线,交直线
于点
,当线段
的长度最大时,求
的值及
的最大值.
(3)在抛物线上是否存在异于
、
的点
,使
中
边上的高为
,若存在求出点
的坐标;若不存在请说明理由.
13.(2019九上·翁牛特旗期中)如图所示,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8),抛物线y=ax2+bx+c(a≠0)与直线y=x﹣4交于B、D两点.
(1)求抛物线的解析式及顶点的坐标;
(2)求D点坐标;
(3)点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标.
14.(2019八下·绿园期末)已知,如图,正方形
的边长为4厘米,点
从点
出发,经
沿正方形的边以2厘米/秒的速度运动;同时,点
从点
出发以1厘米/秒的速度沿
向点
运动,设运动时间为t秒,
的面积为
平方厘米.
(1)当
时,
的面积为________平方厘米;
(2)求
的长(用含
的代数式表示);
(3)当点
在线段
上运动,且
为等腰三角形时,求此时
的值;
(4)求
与
之间的函数关系式.
15.(2019九上·西安月考)在平面直角坐标系中,二次函数
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】
A
2.【答案】
C
3.【答案】
C
4.【答案】
A
5.【答案】
C
二、填空题
6.【答案】
-1<x<6
7.【答案】
(0,4)
8.【答案】
m>﹣3或﹣12<m<﹣4
9.【答案】
9
10.【答案】
②③④
三、综合题
11.【答案】
(1)解:∵抛物线y=ax2+bx+2经过点A(4,0),B(﹣1,0),
∴
,
解得:
,
∴抛物线的解析式为:y=
x2+
x+2;
(2)解:连接OD,由题意知,四边形OFDE是矩形,则OD=EF,据垂线段最短,可知:
?
当OD⊥AC时,OD最短,即EF最短.
由(1)知,在Rt△AOC中,OC=2,OA=4,
∴AC=
.
∵
,
∴
,
故EF的长度为
;
(3)解:假设存在,设点P的坐标为(m,
m2+
m+2).
∵点A的坐标为(4,0),点C的坐标为(0,2),
∴AP2=(m﹣4)2+(
m2+
m+2﹣0)2
,
CP2=(m﹣0)2+(
m2+
m+2﹣2)2
,
AC2=(0﹣4)2+(2﹣0)2=20.
分两种情况考虑,①当∠ACP=90°时,AP2=CP2+AC2
,
即(m﹣4)2+(
m2+
m+2﹣0)2=(m﹣0)2+(
m2+
m+2﹣2)2+20,
解得:m1=0(舍去),m2=-1,
∴点P的坐标为(-1,0);
②当∠APC=90°时,CP2+AP2=AC2
,
即,(m﹣4)2+(
m2+
m+2﹣0)2+(m﹣0)2+(
m2+
m+2﹣2)2=20
解得:m1=0(舍去),m2=4(舍去),m3=m4=1,
∴点P的坐标为(1,3).
综上所述,假设成立,
即存在点P(-1,0)或(1,3),使得△ACP是直角三角形.
12.【答案】
(1)解:
,令
,则
,令
,则
,
故点
、
的坐标分别为
、
,
将
、
代入二次函数表达式为
,
解得:
,
故抛物线的表达式为:
.
(2)解:设
点横坐标为
,则
,
,
,
当
时,PM有最大值
(3)解:如图,过
作
轴交
于点
,交
轴于点
,作
于
,
设
,则
,
,
是等腰直角三角形,
,
,
当
中
边上的高为
时,即
,
,
,
当
时,解得
或
,
或
,
当
时,解得
或
,
或
,
综上可知存在满足条件的点
,其坐标为
,
,
,
.
13.【答案】
(1)解:抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
故﹣8a=﹣8,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣8;
∴
,故顶点坐标为(1,-9)
(2)解:抛物线与直线交于BD两点,
依题意得:
,
解得:
,
,
故点D(﹣1,﹣5);
(3)解:过点P作y轴的平行线交BD于点H,
设点P(x,x2﹣2x﹣8),则点H(x,x﹣4)
△BDP面积=
PH×(xB﹣xD)=
×(x﹣4﹣x2+2x+8)×(4+1)=
,
∵
0,故面积有最大值为:
;
此时,x=
,P点纵坐标为
,
即点P(
,
).
14.【答案】
(1)8
(2)解:分两种情况:
当0≤t≤2时,P在AB上,BP=AB﹣AP=4﹣2t,当2<t≤4时,P在BC上,BP=2t﹣4;
综上所述:BP=
;
(3)解:如图2.
∵△PCQ为等腰三角形,∴CQ=CP,即t=8﹣2t,t
,∴当点P在线段BC上运动,且△PCQ为等腰三角形时,此时t的值是
秒;
(4)解:分两种情况:
①当0≤t≤2时,P在AB上,如图3.
S
4t
②当2<t≤4时,P在BC上,如图4.
S=S正方形ABCD﹣S△ABP﹣S△CPQ﹣S△ADQ=4×4
t2﹣6t+16;
综上所述:S与t之间的函数关系式为:S
.
15.【答案】
(1)由抛物线
过A(-3,0),B(1,0),则
,解得
.
∴二次函数的关系解析式为
.
(2)设点P坐标为(m,n),则
.
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
PM
=
,
,AO=3.
当
时,
,所以OC=2.
∵
<0,∴函数
有最大值,当
时,
有最大值.
此时
.
∴存在点
,使△ACP的面积最大.
(3)如图(3)所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3,则点Q1,Q2,Q3,Q4为符合题意要求的点.
过Q1点作Q1D⊥y轴于点D,
∵∠BCQ1=90°,
∴∠Q1CD+∠OCB=90°,
又∵在直角△OBC中,∠OCB+∠CBO=90°,
∴∠Q1CD=∠OCB,
又∵Q1C=BC,∠Q1DC=∠BOC,
∴△Q1CD≌△CBO,
∴Q1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q1(2,3);
同理求得Q2(3,1),Q3(?1,?1),Q4(?2,1).
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(?1,?1),Q4(?2,1).
(4)如图(4)所示,设E(n,0),则BE=1?n,
.
假设以点B.?Q、E为顶点的三角形与△AOC相似,则有两种情况:
①若△AOC∽△BEQ,则有:
,
即
,化简得:n2+n?2=0,
解得n1=?2,n2=1(与B重合,舍去),
∴n=?2,
.
∴Q(?2,2);
②若△AOC∽△BQE,则有:
,
即
,化简得:4n2?n?3=0,
解得
(与B重合,舍去),
∴
.
综上所述,存在点Q,使以点B.?Q、E为顶点的三角形与△AOC相似.
Q点坐标为(?2,2)或
.
(5)假设存在点Q,使以A.
C.?M、Q为顶点的四边形是平行四边形.
①若CM平行于x轴,如图(5)a所示,有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.
∵CM∥x轴,∴点M、点C(0,2)关于对称轴x=?1对称,
∴M(?2,2),
∴CM=2.
由Q1A=Q2A=CM=2,得到Q1(?5,0),Q2(?1,0);
②若CM不平行于x轴,如图(5)b所示.过点M作MG⊥x轴于G,
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=?2.
设M(x,?2),则有
,
解得
又QG=3,
∴
,
综上所述,存在点Q,使以A.
C.?M、Q为顶点的四边形是平行四边形.Q点坐标为:
.
21世纪教育网(www.21cnjy.com)
同课章节目录
