直线与圆的位置关系复习课
图片预览




文档简介
(共22张PPT)
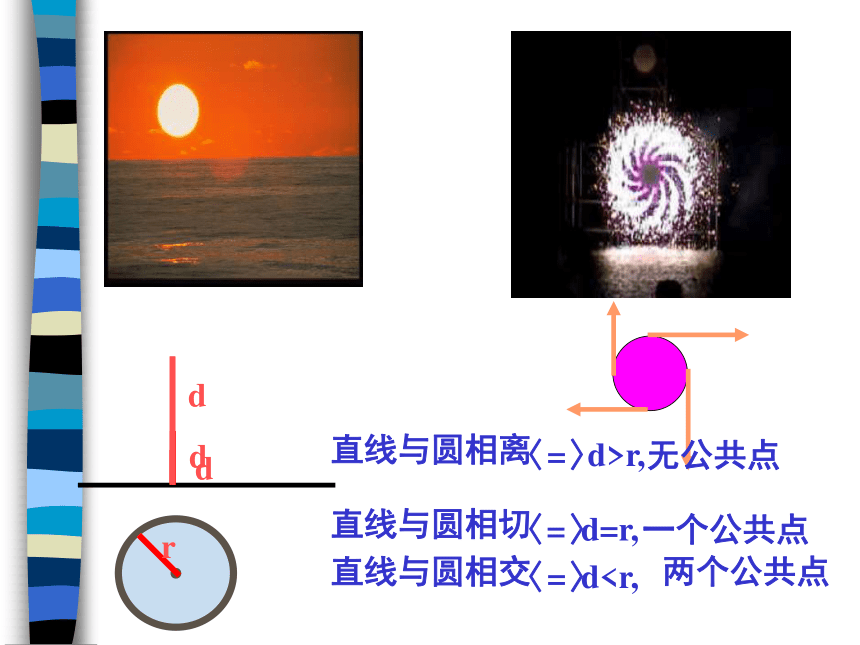
●
r
直线与圆相交
直线与圆相切
直线与圆相离
d>r,
d=r,
d无公共点
一个公共点
两个公共点
〈=〉
〈=〉
〈=〉
d
d
d
2、连结直线外一点与直线所
有点的线段中,最短的是______?
1.直线外一点到这条直线
垂线段的长度叫点到直线 的距离。
垂线段
a
.A
D
什么叫点到直线的距离?
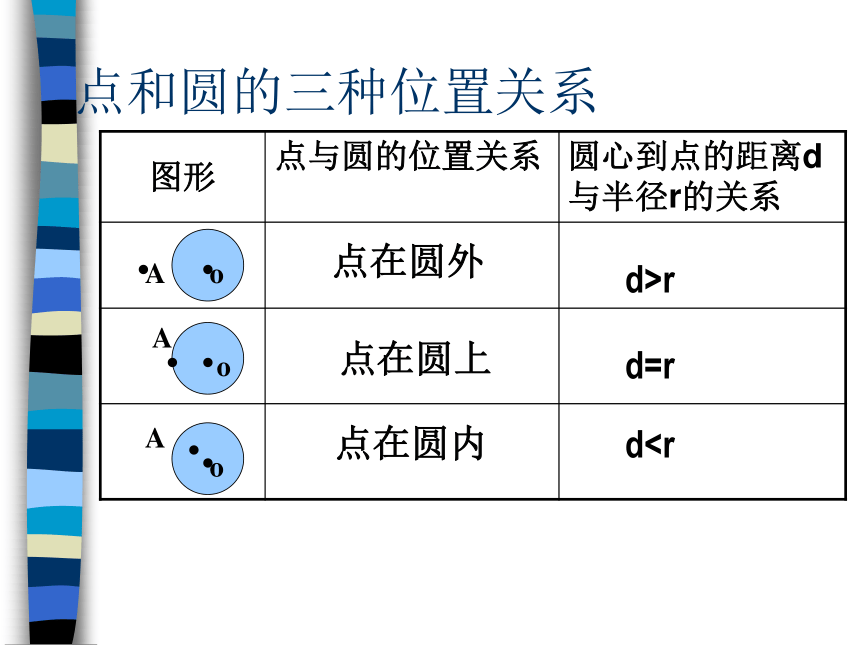
点和圆的三种位置关系
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
A
A
A
o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
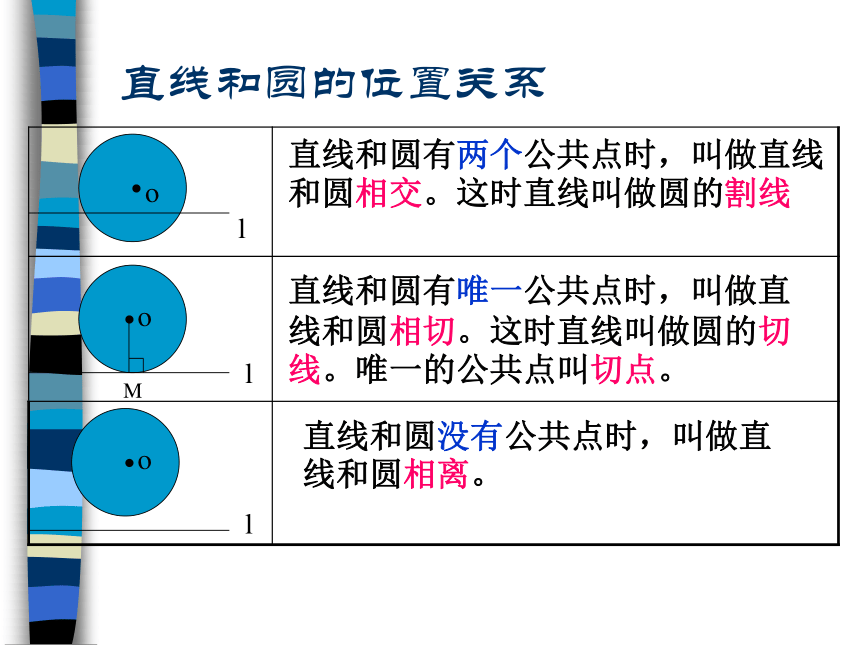
d直线和圆的位置关系
l
l
l
直线和圆有两个公共点时,叫做直线和圆相交。这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切。这时直线叫做圆的切线。唯一的公共点叫切点。
直线和圆没有公共点时,叫做直线和圆相离。
o
o
o
M
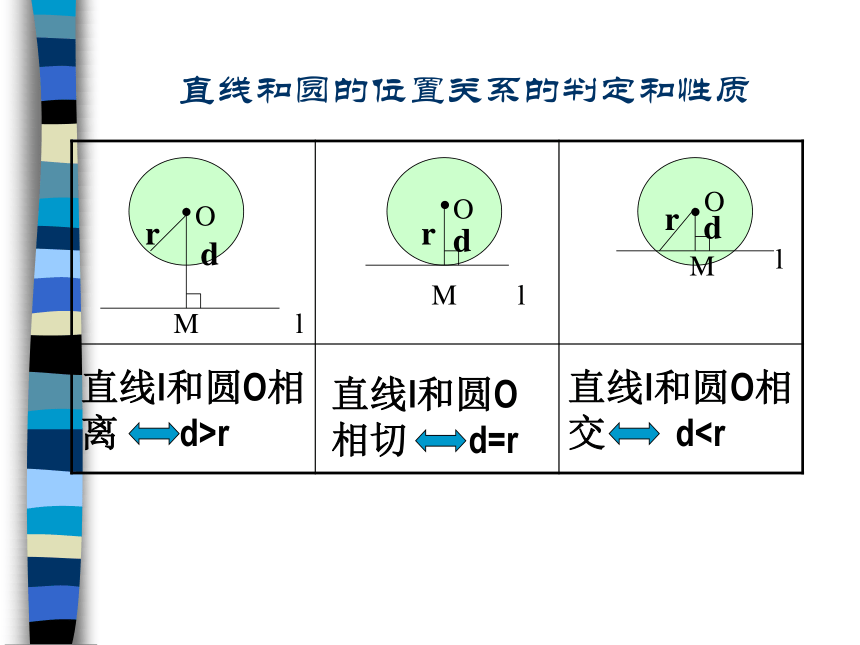
直线和圆的位置关系的判定和性质
O
l
O
O
l
l
M
M
M
直线l和圆O相切 d=r
直线l和圆O相交 d直线l和圆O相离 d>r
d
d
d
r
r
r
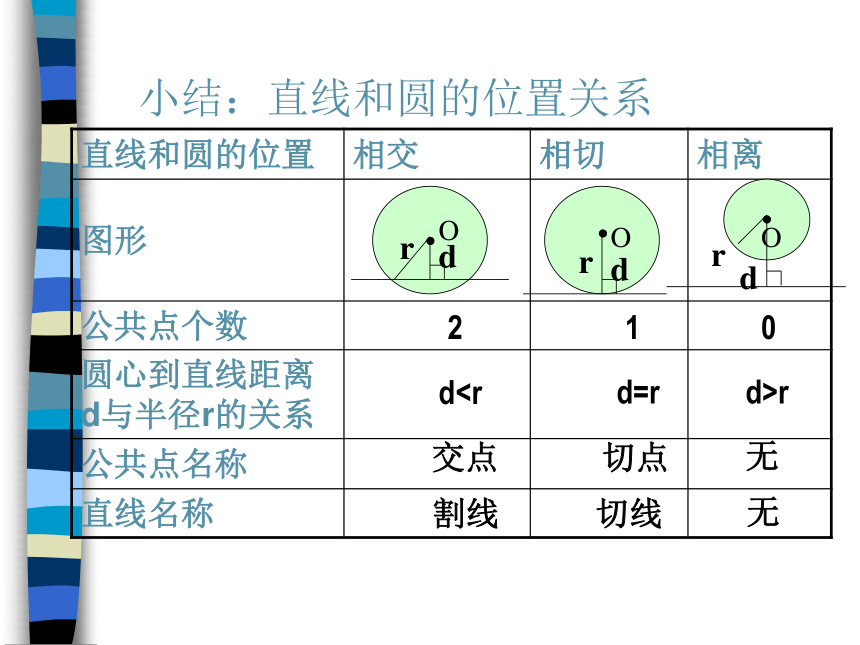
小结:直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
dd=r
d>r
交点
切点
无
割线
切线
无
O
d
r
O
l
d
r
O
d
r
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由_____________
的个数来判断;
(2)根据性质,由______________ ______________的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
下雨天当你快速转动雨伞时飞出的水,在砂轮上打磨工件飞
出的火星,都是沿着圆的切线的方向飞出的.
问题:1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2 砂轮打磨工件飞出火星的方向是什么方向?
1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?
2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___
3.如图,∠APC=50°,PA、PC、DE都为⊙O的切线,则∠DOE为 。
变式:改变切线DE的位置,则∠DOE=___
F
65°
65°
归纳:只要∠APC的大小不变. ∠DOE也不变.
例1、如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G, ⊙O 是△CGF的外接圆
求证:CE是⊙O的切线。
例2如图AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F。
(1)求证:DE是⊙O的切线。
(2)若DE=3,⊙O的半径是5,求BD的长。
1、如图,已知:AB与⊙O相切于点C ,OA=OB,⊙O的直径为6cm ,AB=8cm,则OA=_____cm.
变式:若AB等于6cm,则∠AOB=_______.
5
90°
变直线与圆的位置例题变式.gsp关系有关资料\例题变式.gsp式:
C
如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.
2
变式1:CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△ PCD的周长为____.
4
E
C
D
变式2:改变切点E的位置(在略户AB上),则△ PCD的周长为____.
变式3:若PA=5则△ PCD的周长为____.
4
10
变式4:若PA=a,则△ PCD的周长为____.
2a
(2)⊙O上是否存在点C,使△ PBC为等边三角形?若存在,请求出此时PB的值,若不存在,请说明理由。
例2已知,如图1 A是半径为2的⊙O上一点,P是OA延长线上的动点,过P点作⊙O的切线为B.
(1)当PB=4时,求PO 的值。
C
(3)当PB为何值时,⊙O上存在唯一点M 和PB构成以PB为底的等腰三角形?并直接答出 。此时⊙O上能与PB构成等腰三角形的点共有几个?
连接到直线与例2(3).gsp圆的位置关系有关资料\例2(3).gsp几何画板
1、A村和B村在一条路的两端,这条路经过一条圆湖。因为大桥整修,请你设计一条路线,使得A村到B村的距离最短。
2、在平面直角坐标下,⊙O的半径为2,圆心在原点,已知反比例函数图象y=2/x 与⊙O在第一象限只有一个交点B,
反比例函数图象与⊙O在第三象限也只有一个交点吗?为什么?
你能找到另一个反比例函数,使得在一个象限内与⊙O只能有一个交点。
你能求出点B的坐标吗?
(4) 是否存在经过点B的切线与这两个交点(第(2))所在的直线平行?若存在,求出这条切线,若不存在,请说明理由?
1 今天我们一起复习哪些圆的有关知识?
2 今天我们探究的问题都有什么特点?
3 对今天的问题你还有什么困惑?
4 今天你有什么收获吗?
谢谢指导
●
r
直线与圆相交
直线与圆相切
直线与圆相离
d>r,
d=r,
d
一个公共点
两个公共点
〈=〉
〈=〉
〈=〉
d
d
d
2、连结直线外一点与直线所
有点的线段中,最短的是______?
1.直线外一点到这条直线
垂线段的长度叫点到直线 的距离。
垂线段
a
.A
D
什么叫点到直线的距离?
点和圆的三种位置关系
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
A
A
A
o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
d
l
l
l
直线和圆有两个公共点时,叫做直线和圆相交。这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切。这时直线叫做圆的切线。唯一的公共点叫切点。
直线和圆没有公共点时,叫做直线和圆相离。
o
o
o
M
直线和圆的位置关系的判定和性质
O
l
O
O
l
l
M
M
M
直线l和圆O相切 d=r
直线l和圆O相交 d
d
d
d
r
r
r
小结:直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
d
d>r
交点
切点
无
割线
切线
无
O
d
r
O
l
d
r
O
d
r
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由_____________
的个数来判断;
(2)根据性质,由______________ ______________的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
下雨天当你快速转动雨伞时飞出的水,在砂轮上打磨工件飞
出的火星,都是沿着圆的切线的方向飞出的.
问题:1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2 砂轮打磨工件飞出火星的方向是什么方向?
1如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少?
2 如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___
3.如图,∠APC=50°,PA、PC、DE都为⊙O的切线,则∠DOE为 。
变式:改变切线DE的位置,则∠DOE=___
F
65°
65°
归纳:只要∠APC的大小不变. ∠DOE也不变.
例1、如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G, ⊙O 是△CGF的外接圆
求证:CE是⊙O的切线。
例2如图AB为⊙O的直径,D是弧BC的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于F。
(1)求证:DE是⊙O的切线。
(2)若DE=3,⊙O的半径是5,求BD的长。
1、如图,已知:AB与⊙O相切于点C ,OA=OB,⊙O的直径为6cm ,AB=8cm,则OA=_____cm.
变式:若AB等于6cm,则∠AOB=_______.
5
90°
变直线与圆的位置例题变式.gsp关系有关资料\例题变式.gsp式:
C
如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.
2
变式1:CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△ PCD的周长为____.
4
E
C
D
变式2:改变切点E的位置(在略户AB上),则△ PCD的周长为____.
变式3:若PA=5则△ PCD的周长为____.
4
10
变式4:若PA=a,则△ PCD的周长为____.
2a
(2)⊙O上是否存在点C,使△ PBC为等边三角形?若存在,请求出此时PB的值,若不存在,请说明理由。
例2已知,如图1 A是半径为2的⊙O上一点,P是OA延长线上的动点,过P点作⊙O的切线为B.
(1)当PB=4时,求PO 的值。
C
(3)当PB为何值时,⊙O上存在唯一点M 和PB构成以PB为底的等腰三角形?并直接答出 。此时⊙O上能与PB构成等腰三角形的点共有几个?
连接到直线与例2(3).gsp圆的位置关系有关资料\例2(3).gsp几何画板
1、A村和B村在一条路的两端,这条路经过一条圆湖。因为大桥整修,请你设计一条路线,使得A村到B村的距离最短。
2、在平面直角坐标下,⊙O的半径为2,圆心在原点,已知反比例函数图象y=2/x 与⊙O在第一象限只有一个交点B,
反比例函数图象与⊙O在第三象限也只有一个交点吗?为什么?
你能找到另一个反比例函数,使得在一个象限内与⊙O只能有一个交点。
你能求出点B的坐标吗?
(4) 是否存在经过点B的切线与这两个交点(第(2))所在的直线平行?若存在,求出这条切线,若不存在,请说明理由?
1 今天我们一起复习哪些圆的有关知识?
2 今天我们探究的问题都有什么特点?
3 对今天的问题你还有什么困惑?
4 今天你有什么收获吗?
谢谢指导
