浙教B本八年级上册数学 第4章《图形与坐标》 测试卷(word版有答案)
文档属性
| 名称 | 浙教B本八年级上册数学 第4章《图形与坐标》 测试卷(word版有答案) |  | |
| 格式 | doc | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-06 08:59:55 | ||
图片预览



文档简介
第4章 测试卷
一、选择题(每题3分,共30分)
1.下列各点中,在第三象限的是( )
A.(1,7) B.(-1,-7) C.(1,-7) D.(-1,7)
2.给新同学指路,介绍文具店的位置时,其中表达正确的是( )
A.在学校的右边 B.距学校900 m处
C.在学校的西边 D.在学校的西边距学校900 m处
3.如图,已知棋子“相”的坐标为(-2,3),棋子“兵”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(-2,2)
4.在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于x轴对称,则a+b的值为( )
A.33 B.-33 C.-7 D.7
5.若点P(3,-4),Q(x,-4)之间的距离是5,则x的值为( )
A.-2 B.-2或2 C.8 D.-2或8
6.在平面直角坐标系xOy中,若点A的坐标为(-3,3),点B的坐标为(2,0),则三角形ABO的面积是( )
A.15 B.7.5 C.6 D.3
7.在平面直角坐标系中,点A(1,2)平移后的坐标是A′(-3,3),按照此平移方式平移其他点,则下列变换符合这种要求的是( )
A.(3,2)→ (4,2) B.(-1,0) → (-5,-4)
C. → D.(1.2,5) → (-3.2,6)
8.在平面直角坐标系中,下列各点关于y轴的对称点在第一象限的是( )
A.(2,1) B.(2,-1) C.(-2,1) D.(-2,-1)
9.如图,A,B两点的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3 C.4 D.5
10.在平面直角坐标系xOy中,已知点A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.下列结论:①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;④点(1,1)在第二象限;⑤点(2,0)在x轴的正半轴上.
其中正确的是________.(填序号)
12.某市区有3个自行车站点,位置如图所示,若站点1的位置表示为(B,1),站点2的位置表示为(C,3),则站点3的位置可表示为____________.
13.若点A(3,x-1)在x轴上,点B(2y+2,1)在y轴上,则x2+y2的值为________.
14.在平面直角坐标系中,点A(-3,2)关于x轴对称的点B,将点B向右平移3个单位得到点C,则点C的坐标是________.
15.如图,在平面直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5,则线段AB上任意一点的坐标可以用“(x,-1)(1≤x≤5)”表示.若射线CD垂直平分AB于点C,那么按照类似这样的规定,射线CD上任意一点的坐标可以表示为____________.
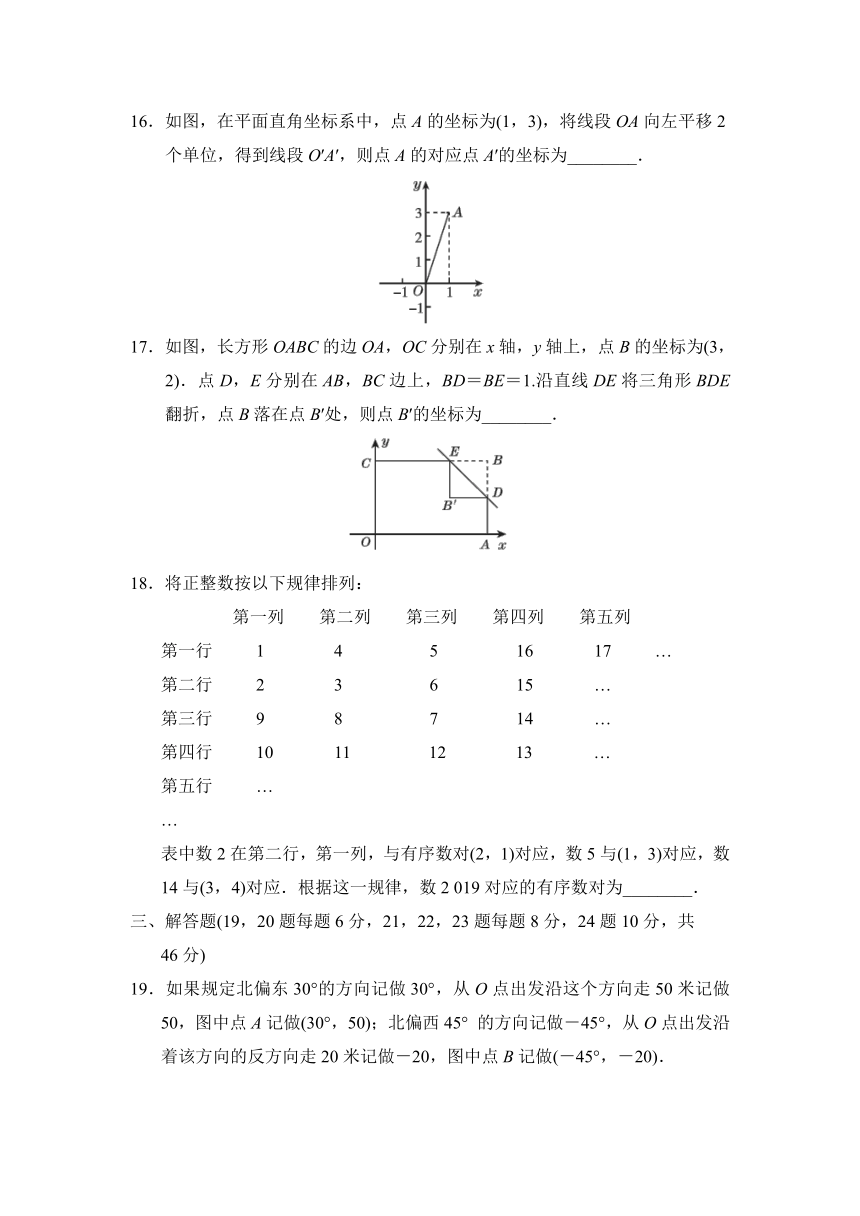
16.如图,在平面直角坐标系中,点A的坐标为(1,3),将线段OA向左平移2个单位,得到线段O′A′,则点A的对应点A′的坐标为________.
17.如图,长方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(3,2).点D,E分别在AB,BC边上,BD=BE=1.沿直线DE将三角形BDE翻折,点B落在点B′处,则点B′的坐标为________.
18.将正整数按以下规律排列:
第一列 第二列 第三列 第四列 第五列
第一行 1 4 5 16 17 …
第二行 2 3 6 15 …
第三行 9 8 7 14 …
第四行 10 11 12 13 …
第五行 …
…
表中数2在第二行,第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应.根据这一规律,数2 019对应的有序数对为________.
三、解答题(19,20题每题6分,21,22,23题每题8分,24题10分,共
46分)
19.如果规定北偏东30°的方向记做30°,从O点出发沿这个方向走50米记做50,图中点A记做(30°,50);北偏西45° 的方向记做-45°,从O点出发沿着该方向的反方向走20米记做-20,图中点B记做(-45°,-20).
(1)(-75°,-15),(10°,-25)分别表示什么意义?
(2)在图中标出点(60°,-30)和(-30°,40).
20.根据下列条件建立适当的直角坐标系,标出学校、少年宫、体育馆、新华书店的位置.
从学校向东走300 m,再向北走300 m是少年宫;
从学校向西走100 m,再向北走200 m是体育馆;
从学校向南走150 m,再向东走250 m,再向南走50 m是新华书店.
21.已知点P(2x,3x-1)是平面直角坐标系内的点.
(1)若点P在第一象限的角平分线上,求x的值;
(2)若点P在第三象限,且到两坐标轴的距离之和为16,求x的值.
22.如图,已知A(0,4),B(-2,2),C(3,0).
(1)作△ABC关于x轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标A1(________),B1(________),C1(________);
(3)△A1B1C1的面积为________.
23.如图,梯形ABCD是直角梯形.
(1)直接写出点A,B,C,D的坐标;
(2)画出直角梯形ABCD关于y轴的对称图形;
(3)直角梯形ABCD与其关于y轴的对称图形构成一个等腰梯形,将这个等腰梯形向上平移4个单位,画出平移后的图形.(不写画法)
24.如图,在平面直角坐标系中,A,B,C三点的坐标分别为(0,1),(2,0),(2,1.5).
(1)求△ABC的面积.
(2)如果在第二象限内有一点P(a,),试用含a的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
答案
一、1.B
2.D
3.A
4.B 点拨:因为P,Q关于x轴对称,所以a=-13,b=-20,所以a+b=-33.
5.D
6.D 点拨:此题首先运用数形结合思想,在平面直角坐标系中描点连线画出三角形ABO,然后运用转化思想将点的坐标转化为线段的长度,底BO=2,BO边上的高为3,所以三角形ABO的面积=×2×3=3.
7.C
8.C
9.A 点拨:由A点的横坐标的变化可知线段AB向右平移了1个单位,由B点的纵坐标的变化可知线段AB向上平移了1个单位.
10.D 点拨:本题利用分类讨论思想.当OA为等腰三角形的腰时,以O为圆心,OA为半径的圆与y轴有两个交点,以A为圆心,AO为半径的圆与y轴除点O外还有一个交点;当OA为等腰三角形的底时,作线段OA的垂直平分线,与y轴有一个交点.∴符合条件的点一共有4个.故选D.
二、11.③⑤ 点拨:两个点的横纵坐标均不相等,表示的不是同一个点,所以①错误;横坐标为0的点在y轴上,所以②错误;第二象限的点的符号的特征是(-,+),所以④错误.
12.(D,2)
13.2
14.(0,-2)
15.(3,y)(y≥-1)
16.(-1,3)
17.(2,1) 点拨:由题意知四边形BEB′D是正方形,∴点B′的横坐标与点E的横坐标相同,点B′的纵坐标与点D的纵坐标相同,∴点B′的坐标为(2,1).
18.(45,7)
三、19.解:(1)(-75°,-15)表示南偏东75°距O点15米处,(10°,-25)表示南偏西10°距O点25米处.
(2)略.
20.解:选取学校所在的位置为原点,以正东方向为x轴的正方向,以正北方向为y轴的正方向建立平面直角坐标系,学校、少年宫、体育馆、新华书店的位置如图所示.
21.解:(1)由题意得2x=3x-1,
解得x=1.
(2)∵点P(2x,3x-1)在第三象限,
∴∴x<0,∴点P(2x,3x-1)到坐标轴的距离之和为|2x|+|3x-1|=-2x-3x+1=16,解得x=-3.
22.解:(1)如图.
(2)0,-4;-2,-2;3,0
(3)7
23.解:(1)点A,B,C,D的坐标分别为(-2,-1),(-4,-4),(0,-4),
(0,-1).
(2)略. (3)略.
24.解:(1)由点B(2,0),点C(2,1.5),可知CB⊥x轴.过点A作AD⊥BC,垂足为D,则S△ABC=BC·AD=×1.5×2=1.5.
(2)过点P作PE⊥y轴,垂足为E.则S四边形ABOP=S△AOB+S△AOP=AO·OB+AO·PE=×1×2+×1×(-a)=1-a.
(3)存在点P,使得四边形ABOP的面积与△ABC的面积相等.
依题意,得1-a=1.5,解得a=-1.所以存在点P(-1,),使得四边形ABOP的面积与△ABC的面积相等.
一、选择题(每题3分,共30分)
1.下列各点中,在第三象限的是( )
A.(1,7) B.(-1,-7) C.(1,-7) D.(-1,7)
2.给新同学指路,介绍文具店的位置时,其中表达正确的是( )
A.在学校的右边 B.距学校900 m处
C.在学校的西边 D.在学校的西边距学校900 m处
3.如图,已知棋子“相”的坐标为(-2,3),棋子“兵”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(-2,2)
4.在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于x轴对称,则a+b的值为( )
A.33 B.-33 C.-7 D.7
5.若点P(3,-4),Q(x,-4)之间的距离是5,则x的值为( )
A.-2 B.-2或2 C.8 D.-2或8
6.在平面直角坐标系xOy中,若点A的坐标为(-3,3),点B的坐标为(2,0),则三角形ABO的面积是( )
A.15 B.7.5 C.6 D.3
7.在平面直角坐标系中,点A(1,2)平移后的坐标是A′(-3,3),按照此平移方式平移其他点,则下列变换符合这种要求的是( )
A.(3,2)→ (4,2) B.(-1,0) → (-5,-4)
C. → D.(1.2,5) → (-3.2,6)
8.在平面直角坐标系中,下列各点关于y轴的对称点在第一象限的是( )
A.(2,1) B.(2,-1) C.(-2,1) D.(-2,-1)
9.如图,A,B两点的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3 C.4 D.5
10.在平面直角坐标系xOy中,已知点A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.下列结论:①点(3,2)与(2,3)是同一个点;②点(0,-2)在x轴上;③点(0,0)是坐标原点;④点(1,1)在第二象限;⑤点(2,0)在x轴的正半轴上.
其中正确的是________.(填序号)
12.某市区有3个自行车站点,位置如图所示,若站点1的位置表示为(B,1),站点2的位置表示为(C,3),则站点3的位置可表示为____________.
13.若点A(3,x-1)在x轴上,点B(2y+2,1)在y轴上,则x2+y2的值为________.
14.在平面直角坐标系中,点A(-3,2)关于x轴对称的点B,将点B向右平移3个单位得到点C,则点C的坐标是________.
15.如图,在平面直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x≤5,则线段AB上任意一点的坐标可以用“(x,-1)(1≤x≤5)”表示.若射线CD垂直平分AB于点C,那么按照类似这样的规定,射线CD上任意一点的坐标可以表示为____________.
16.如图,在平面直角坐标系中,点A的坐标为(1,3),将线段OA向左平移2个单位,得到线段O′A′,则点A的对应点A′的坐标为________.
17.如图,长方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(3,2).点D,E分别在AB,BC边上,BD=BE=1.沿直线DE将三角形BDE翻折,点B落在点B′处,则点B′的坐标为________.
18.将正整数按以下规律排列:
第一列 第二列 第三列 第四列 第五列
第一行 1 4 5 16 17 …
第二行 2 3 6 15 …
第三行 9 8 7 14 …
第四行 10 11 12 13 …
第五行 …
…
表中数2在第二行,第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应.根据这一规律,数2 019对应的有序数对为________.
三、解答题(19,20题每题6分,21,22,23题每题8分,24题10分,共
46分)
19.如果规定北偏东30°的方向记做30°,从O点出发沿这个方向走50米记做50,图中点A记做(30°,50);北偏西45° 的方向记做-45°,从O点出发沿着该方向的反方向走20米记做-20,图中点B记做(-45°,-20).
(1)(-75°,-15),(10°,-25)分别表示什么意义?
(2)在图中标出点(60°,-30)和(-30°,40).
20.根据下列条件建立适当的直角坐标系,标出学校、少年宫、体育馆、新华书店的位置.
从学校向东走300 m,再向北走300 m是少年宫;
从学校向西走100 m,再向北走200 m是体育馆;
从学校向南走150 m,再向东走250 m,再向南走50 m是新华书店.
21.已知点P(2x,3x-1)是平面直角坐标系内的点.
(1)若点P在第一象限的角平分线上,求x的值;
(2)若点P在第三象限,且到两坐标轴的距离之和为16,求x的值.
22.如图,已知A(0,4),B(-2,2),C(3,0).
(1)作△ABC关于x轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标A1(________),B1(________),C1(________);
(3)△A1B1C1的面积为________.
23.如图,梯形ABCD是直角梯形.
(1)直接写出点A,B,C,D的坐标;
(2)画出直角梯形ABCD关于y轴的对称图形;
(3)直角梯形ABCD与其关于y轴的对称图形构成一个等腰梯形,将这个等腰梯形向上平移4个单位,画出平移后的图形.(不写画法)
24.如图,在平面直角坐标系中,A,B,C三点的坐标分别为(0,1),(2,0),(2,1.5).
(1)求△ABC的面积.
(2)如果在第二象限内有一点P(a,),试用含a的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
答案
一、1.B
2.D
3.A
4.B 点拨:因为P,Q关于x轴对称,所以a=-13,b=-20,所以a+b=-33.
5.D
6.D 点拨:此题首先运用数形结合思想,在平面直角坐标系中描点连线画出三角形ABO,然后运用转化思想将点的坐标转化为线段的长度,底BO=2,BO边上的高为3,所以三角形ABO的面积=×2×3=3.
7.C
8.C
9.A 点拨:由A点的横坐标的变化可知线段AB向右平移了1个单位,由B点的纵坐标的变化可知线段AB向上平移了1个单位.
10.D 点拨:本题利用分类讨论思想.当OA为等腰三角形的腰时,以O为圆心,OA为半径的圆与y轴有两个交点,以A为圆心,AO为半径的圆与y轴除点O外还有一个交点;当OA为等腰三角形的底时,作线段OA的垂直平分线,与y轴有一个交点.∴符合条件的点一共有4个.故选D.
二、11.③⑤ 点拨:两个点的横纵坐标均不相等,表示的不是同一个点,所以①错误;横坐标为0的点在y轴上,所以②错误;第二象限的点的符号的特征是(-,+),所以④错误.
12.(D,2)
13.2
14.(0,-2)
15.(3,y)(y≥-1)
16.(-1,3)
17.(2,1) 点拨:由题意知四边形BEB′D是正方形,∴点B′的横坐标与点E的横坐标相同,点B′的纵坐标与点D的纵坐标相同,∴点B′的坐标为(2,1).
18.(45,7)
三、19.解:(1)(-75°,-15)表示南偏东75°距O点15米处,(10°,-25)表示南偏西10°距O点25米处.
(2)略.
20.解:选取学校所在的位置为原点,以正东方向为x轴的正方向,以正北方向为y轴的正方向建立平面直角坐标系,学校、少年宫、体育馆、新华书店的位置如图所示.
21.解:(1)由题意得2x=3x-1,
解得x=1.
(2)∵点P(2x,3x-1)在第三象限,
∴∴x<0,∴点P(2x,3x-1)到坐标轴的距离之和为|2x|+|3x-1|=-2x-3x+1=16,解得x=-3.
22.解:(1)如图.
(2)0,-4;-2,-2;3,0
(3)7
23.解:(1)点A,B,C,D的坐标分别为(-2,-1),(-4,-4),(0,-4),
(0,-1).
(2)略. (3)略.
24.解:(1)由点B(2,0),点C(2,1.5),可知CB⊥x轴.过点A作AD⊥BC,垂足为D,则S△ABC=BC·AD=×1.5×2=1.5.
(2)过点P作PE⊥y轴,垂足为E.则S四边形ABOP=S△AOB+S△AOP=AO·OB+AO·PE=×1×2+×1×(-a)=1-a.
(3)存在点P,使得四边形ABOP的面积与△ABC的面积相等.
依题意,得1-a=1.5,解得a=-1.所以存在点P(-1,),使得四边形ABOP的面积与△ABC的面积相等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
