2.7 探索勾股定理---同步课件 2021-2022学年浙教版数学八年级上册(24张PPT)
文档属性
| 名称 | 2.7 探索勾股定理---同步课件 2021-2022学年浙教版数学八年级上册(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 648.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-07 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第2章
特殊三角形
第7节
探究勾股定理
第24届国际数学家大会会标
情景导入
一、勾股定理
【做一做】
c
a
b
c
a
b
c
a
b
c
a
b
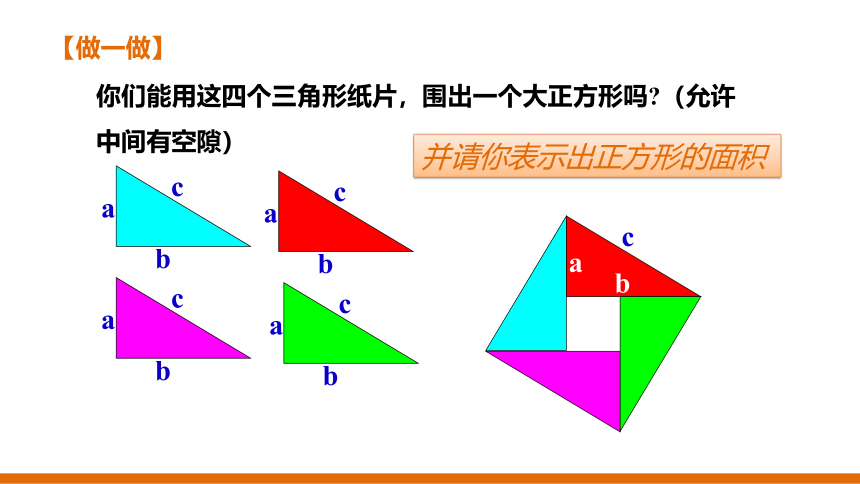
你们能用这四个三角形纸片,围出一个大正方形吗?(允许中间有空隙)
并请你表示出正方形的面积
c
c
c
b
a
b
获取新知
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
a2+b2=c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
中国数学家赵爽根据弦图给出了勾股定理的一种证明
勾
股
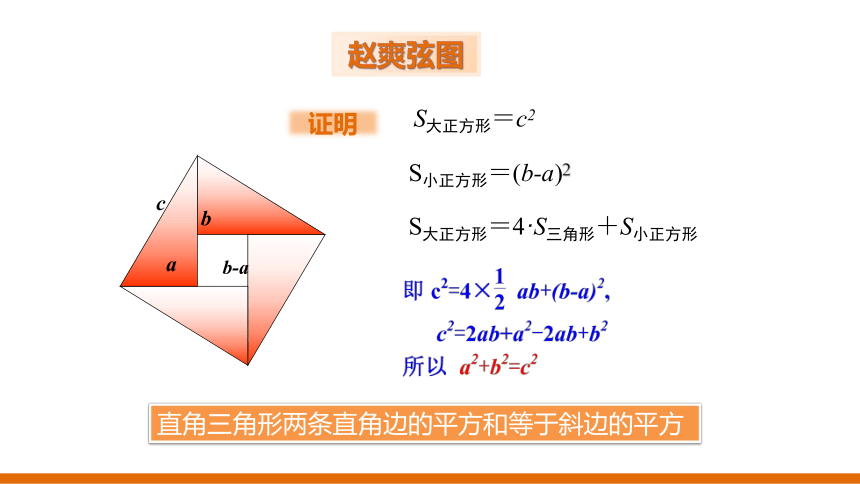
赵爽弦图
a
b
c
b-a
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
证明
直角三角形两条直角边的平方和等于斜边的平方
大正方形的面积可以表示为
;
也可以表示为
.
(a+b)2
c2
+4?ab/2
∵
(a+b)2
=
c2
+
4?ab/2
a2+2ab+b2
=
c2
+2ab
∴
a2+b2=c2
用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
a
a
a
a
b
b
b
b
c
c
c
c
例题精讲
例1
(1)若a=3,
b=2,
求c;
已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c.
(2)若a=15,c=17,求b;
解
(1)∵a∶b=2∶1,∴a=2b.
又∵∠C=90°,c=5,
∴由勾股定理,得(2b)2+b2=52,解得b=
例2
如图是长方形零件图,根据所给的尺寸(单位:mm),
求两孔中心A,B之间的距离.
A
B
C
90
40
160
40
解
过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°,
AC=90-40=50(mm),
BC=160-40=120(mm).
由勾股定理,得
AB2=
AC2+
BC2=502+1202=16900(mm2).
∵AB>0,
∴AB=130(mm).
答:两孔中心A,B之间的距离为130mm.
课堂小结
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边,以及另
两条边之间的关系,
就可以求另两条边的
长度.
随堂演练
1.在Rt△ABC中,∠A=90°,a,b,c分别为∠A,∠B,∠C的对边,a=13
cm,b=5
cm,则c为(
)
A.18
cm
B.12
cm
C.8
cm
D.6
cm
2.等腰三角形的腰长为10,底边长为12,则这个等腰三角
形的面积为(
)
A.36
B.48
C.56
D.64
3.
已知直角三角形的两边长分别为3,4,求第三边的长.
错解:
第三边的长为
(1)当两直角边长分别为3和4时,第三边的长
为
(2)当斜边长为4,一直角边长为3时,第三边
的长为
正确解法:
知识回顾
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
a2+b2=c2
你能说出它的逆定理吗?
二、勾股定理的逆定理
1.画一画:画出边长分别是下列各组数的三角形(单位:厘米)
:
①6,
8,
10;
②
2.5
,
6,
6.5.
2.测一测:用量角器分别测量一下上述各三角形的最大度数:
1:_______
2:_______
3.判断:请判断一下上述你所画的三角形的形状.
A:______
B:_______
直角三角形
直角三角形
【合作学习】
5.猜想:
如果三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形
三边
6
8
10
2.5
6
6.5
36,64,100
36+64=100
各边的平方
规律
?
6.25,36,42.25
6.25+36=42.25
a
b
c
.
4.找一找:寻找三角形三边之间的关系.
如果三角形中
有两边的平方和
等于第三边的平方,那么这个三角形是直角三角形.
∵
△ABC
是直角三角形
a
b
c
最长边所对的角是直角
较短两边的平方和
最长边的平方
直角三角形的判定
获取新知
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
求证:
△ABC是直角三角形.
≌
这种方法我们把它叫做同一法
例题精讲
例1
根据下列条件,分别判断以a,b,c为边的△ABC是不是直角三角形,如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
(2)
1、先求各边的平方
2、观察较短两边的平方和
与最长边的平方
3、判断是否相等
解(1)
为边的三角形是直角三角形.
(2)
也就是较小的两边的平方和都不等于较大边的平方,
∴a,b,c中任何两边的平方和都不等于第三边的平方,
∴以
为边的三角形不是直角三角形.
例2
已知△ABC三条边长分别为a,b,c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)。△ABC是直角三角形吗?请说明理由.
解:∵
a=m2-n2,b=2mn,c=m2+n2
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=(m2+n2)2
=m4+2m2n2+n4
=c2
∴△ABC是直角三角形
课堂小结
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
a
c
b
A
B
C
(1)
如果三角形两边的平方和等于第三边平方,
那么这个三角形是直角三角形.
直角三角形的判定方法之一:
a2+b2=c2
1.下列四组长度的线段中,可以构成直角三角形的是(
)
A.1,2,3
B.2,3,4
C.3,4,5
D.4,5,6
2.已知在△ABC中,AB=8,BC=6,AC=10,则下列说法中错
误的是(
)
A.△ABC是直角三角形,且AC为斜边
B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积为24
D.△ABC是直角三角形,且∠BAC=60°
随堂演练
3.如图,以△ABC的每一条边为边作三个正方形。已知这三个正方形构成的图形中,灰色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗?请说明理由。
第2章
特殊三角形
第7节
探究勾股定理
第24届国际数学家大会会标
情景导入
一、勾股定理
【做一做】
c
a
b
c
a
b
c
a
b
c
a
b
你们能用这四个三角形纸片,围出一个大正方形吗?(允许中间有空隙)
并请你表示出正方形的面积
c
c
c
b
a
b
获取新知
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
a2+b2=c2
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
中国数学家赵爽根据弦图给出了勾股定理的一种证明
勾
股
赵爽弦图
a
b
c
b-a
S大正方形=c2
S小正方形=(b-a)2
S大正方形=4·S三角形+S小正方形
证明
直角三角形两条直角边的平方和等于斜边的平方
大正方形的面积可以表示为
;
也可以表示为
.
(a+b)2
c2
+4?ab/2
∵
(a+b)2
=
c2
+
4?ab/2
a2+2ab+b2
=
c2
+2ab
∴
a2+b2=c2
用四个全等的直角三角形,还可以拼成如图所示的图形,你能否根据这一图形,证明勾股定理.
a
a
a
a
b
b
b
b
c
c
c
c
例题精讲
例1
(1)若a=3,
b=2,
求c;
已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c.
(2)若a=15,c=17,求b;
解
(1)∵a∶b=2∶1,∴a=2b.
又∵∠C=90°,c=5,
∴由勾股定理,得(2b)2+b2=52,解得b=
例2
如图是长方形零件图,根据所给的尺寸(单位:mm),
求两孔中心A,B之间的距离.
A
B
C
90
40
160
40
解
过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°,
AC=90-40=50(mm),
BC=160-40=120(mm).
由勾股定理,得
AB2=
AC2+
BC2=502+1202=16900(mm2).
∵AB>0,
∴AB=130(mm).
答:两孔中心A,B之间的距离为130mm.
课堂小结
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边,以及另
两条边之间的关系,
就可以求另两条边的
长度.
随堂演练
1.在Rt△ABC中,∠A=90°,a,b,c分别为∠A,∠B,∠C的对边,a=13
cm,b=5
cm,则c为(
)
A.18
cm
B.12
cm
C.8
cm
D.6
cm
2.等腰三角形的腰长为10,底边长为12,则这个等腰三角
形的面积为(
)
A.36
B.48
C.56
D.64
3.
已知直角三角形的两边长分别为3,4,求第三边的长.
错解:
第三边的长为
(1)当两直角边长分别为3和4时,第三边的长
为
(2)当斜边长为4,一直角边长为3时,第三边
的长为
正确解法:
知识回顾
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
a2+b2=c2
你能说出它的逆定理吗?
二、勾股定理的逆定理
1.画一画:画出边长分别是下列各组数的三角形(单位:厘米)
:
①6,
8,
10;
②
2.5
,
6,
6.5.
2.测一测:用量角器分别测量一下上述各三角形的最大度数:
1:_______
2:_______
3.判断:请判断一下上述你所画的三角形的形状.
A:______
B:_______
直角三角形
直角三角形
【合作学习】
5.猜想:
如果三角形中有两边的平方和等于第三边的平方,那么这个三角形是直角三角形
三边
6
8
10
2.5
6
6.5
36,64,100
36+64=100
各边的平方
规律
?
6.25,36,42.25
6.25+36=42.25
a
b
c
.
4.找一找:寻找三角形三边之间的关系.
如果三角形中
有两边的平方和
等于第三边的平方,那么这个三角形是直角三角形.
∵
△ABC
是直角三角形
a
b
c
最长边所对的角是直角
较短两边的平方和
最长边的平方
直角三角形的判定
获取新知
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
求证:
△ABC是直角三角形.
≌
这种方法我们把它叫做同一法
例题精讲
例1
根据下列条件,分别判断以a,b,c为边的△ABC是不是直角三角形,如果是,指出哪条边所对的角是直角.
(1)a=7,b=24,c=25;
(2)
1、先求各边的平方
2、观察较短两边的平方和
与最长边的平方
3、判断是否相等
解(1)
为边的三角形是直角三角形.
(2)
也就是较小的两边的平方和都不等于较大边的平方,
∴a,b,c中任何两边的平方和都不等于第三边的平方,
∴以
为边的三角形不是直角三角形.
例2
已知△ABC三条边长分别为a,b,c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)。△ABC是直角三角形吗?请说明理由.
解:∵
a=m2-n2,b=2mn,c=m2+n2
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=(m2+n2)2
=m4+2m2n2+n4
=c2
∴△ABC是直角三角形
课堂小结
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
a
c
b
A
B
C
(1)
如果三角形两边的平方和等于第三边平方,
那么这个三角形是直角三角形.
直角三角形的判定方法之一:
a2+b2=c2
1.下列四组长度的线段中,可以构成直角三角形的是(
)
A.1,2,3
B.2,3,4
C.3,4,5
D.4,5,6
2.已知在△ABC中,AB=8,BC=6,AC=10,则下列说法中错
误的是(
)
A.△ABC是直角三角形,且AC为斜边
B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积为24
D.△ABC是直角三角形,且∠BAC=60°
随堂演练
3.如图,以△ABC的每一条边为边作三个正方形。已知这三个正方形构成的图形中,灰色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗?请说明理由。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
