1.3 绝对值 课件(共16张PPT)
图片预览



文档简介
(共16张PPT)
1.3绝对值
浙教版
七年级上
旧知温顾
1.什么是数轴?
规定了原点、正方向、单位长度的直线.
三要素
2.什么相反数?
只有符号不同的两个数互为相反数.
特别地,0的相反数是0.
3.在数轴上,表示互为相反数(0除外)的两个点有什么特征?
位于原点的两侧,并且到原点的距离相等.
新知导入
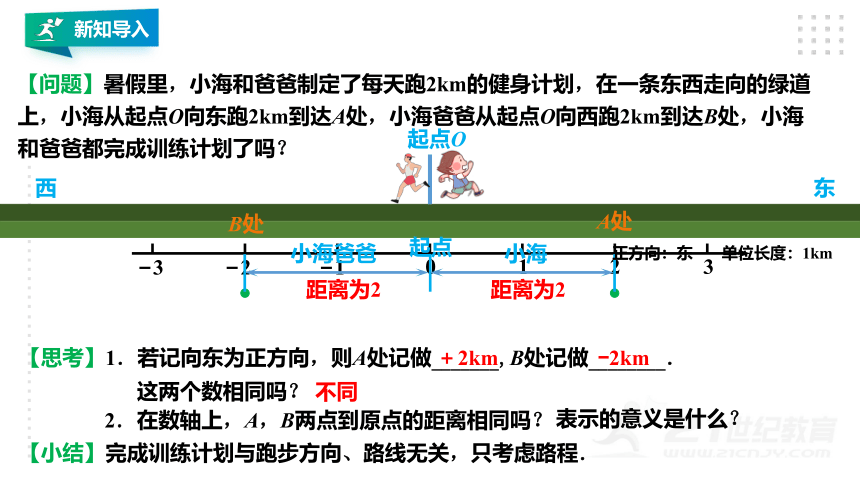
【问题】暑假里,小海和爸爸制定了每天跑2km的健身计划,在一条东西走向的绿道上,小海从起点O向东跑2km到达A处,小海爸爸从起点O向西跑2km到达B处,小海和爸爸都完成训练计划了吗?
起点O
0
1
2
3
?1
?2
?3
东
西
A处
B处
【思考】1.若记向东为正方向,则A处记做_______,B处记做________.
2.在数轴上,A,B两点到原点的距离相同吗?
+2km
?2km
这两个数相同吗?
不同
小海爸爸
起点
小海
正方向:东
单位长度:1km
距离为2
距离为2
表示的意义是什么?
【小结】完成训练计划与跑步方向、路线无关,只考虑路程.
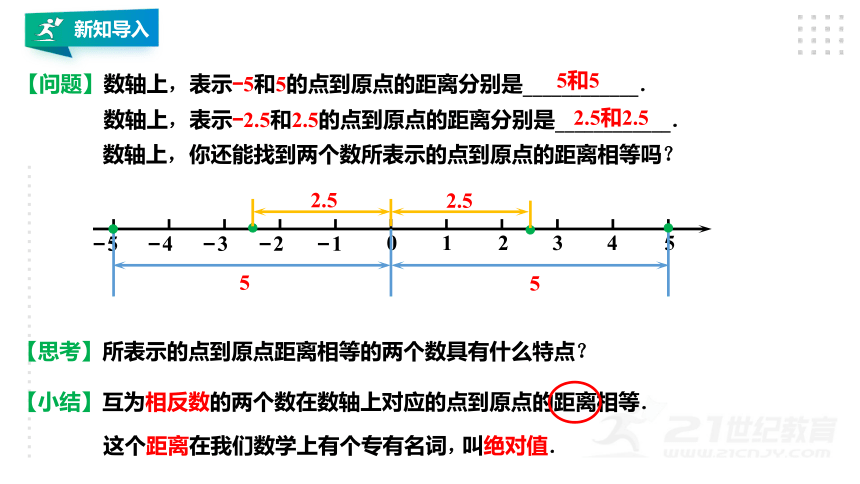
【问题】数轴上,表示?5和5的点到原点的距离分别是____________.
数轴上,表示?2.5和2.5的点到原点的距离分别是____________.
5和5
2.5和2.5
0
1
2
3
4
?1
?2
?3
?4
5
?5
5
5
2.5
2.5
数轴上,你还能找到两个数所表示的点到原点的距离相等吗?
【思考】所表示的点到原点距离相等的两个数具有什么特点?
【小结】互为相反数的两个数在数轴上对应的点到原点的距离相等.
这个距离在我们数学上有个专有名词,
叫绝对值.
新知导入
新知讲解
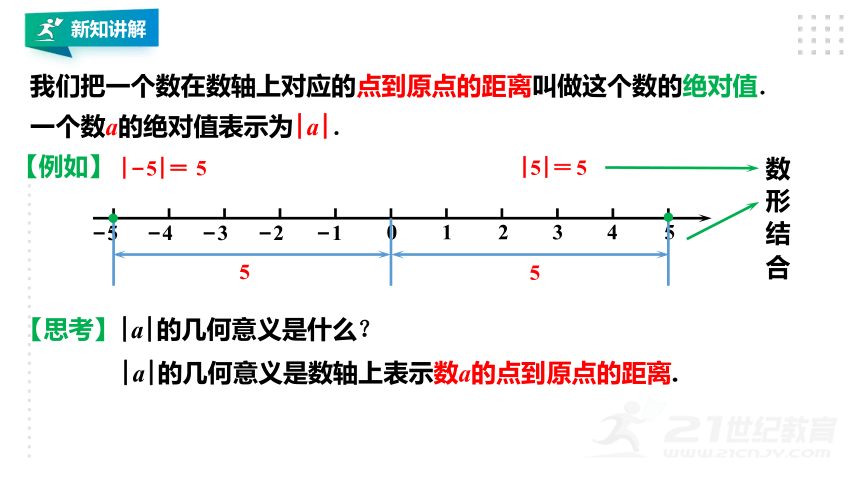
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
一个数a的绝对值表示为|a|.
0
1
2
3
4
?1
?2
?3
?4
5
?5
5
5
【例如】
|?5|=
5
|5|=
5
【思考】|a|的几何意义是什么?
数
形
结合
|a|的几何意义是数轴上表示数a的点到原点的距离.
例题解析
例1
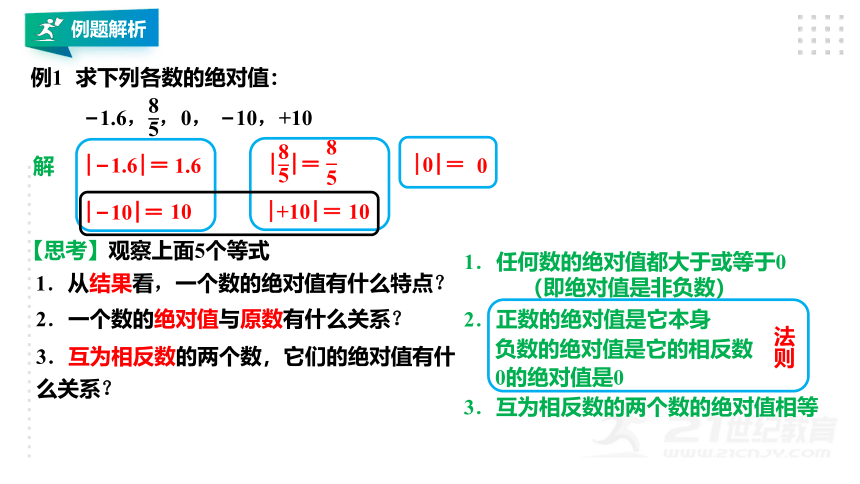
求下列各数的绝对值:
?1.6,,0,
?10,+10
|?1.6|=
1.6
解
||=
|0|=
0
|?10|=
10
|+10|=
10
【思考】观察上面5个等式
1.从结果看,一个数的绝对值有什么特点?
1.任何数的绝对值都大于或等于0
(即绝对值是非负数)
2.一个数的绝对值与原数有什么关系?
2.正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
3.互为相反数的两个数,它们的绝对值有什么关系?
3.互为相反数的两个数的绝对值相等
法则
例题解析
例2
求绝对值等于4的数.
解:
因为数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和表示?4的点M,所以绝对值等于4的数是+4和?4.
几何意义?
0
1
2
3
4
?1
?2
?3
?4
5
?5
4个单位长度
4个单位长度
P
M
方法(一)
方法(二)
因为|+4|=4,|?4|=4,
所以绝对值等于4的数是+4和?4.
课堂练习
1.判断:
(1)一个数的绝对值是
2,则这数是2.
(2)|5|=|?5|.
(3)|?0.3|=|0.3|.
(4)|3|>0.
(5)|?1.4|>0.
(6)有理数的绝对值一定是正数.
(7)若a=b,则|a|=|b|.
(8)若|a|=|b|,则a=b.
(9)若|a|=?a,则a必为负数.
(10)互为相反数的两个数的绝对值相等.
课堂练习
2.计算:
(1)|5?1|=(
).
(2)1+|?5|=(
).
(3)|5|?|?3|=(
).
(4)|?1|
+
|?2|=(
).
(5)|+3|?|?3|=
(
).
4
6
2
3
0
3.下列说法中,正确的是( )
(A)最小的有理数是0
(B)最小的正整数是0
(C)绝对值最小的负数是?1
(D)绝对值最小的有理数是0
D
课堂练习
6.绝对值小于3的整数有_____个,分别是_____________________.
7.绝对值不大于5的整数中,最大的数是_____,最小的数是_____.
4.绝对值等于2的数是_________.
2或?2
5.一个数的绝对值是它本身,那么这个数是__________.
正数或0
(非负数)
5
?2、?1、0、1、2
5
?5
8.如图,图中数轴的单位长度为1.如果点B,C所表示的数的绝对值相
等,那么点A表示的数是________.
?5
拓展提升
1.若|a|+|b|=0
,则a=_____,b=
_____
.
0
0
2.已知|x?2|+|y?1|=0
,则x+y=
_____
.
2
3.计算:|?1|+|?
|+|?
|+…+|?
|
解:原式=++?+…+?
=?
=
课堂总结
绝对值
概念
性质
法则
应用
一个数在数轴上对应的点到原点的距离
符号
|
|
任何数的绝对值都大于或等于0
互为相反数的两个数的绝对值相等
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
直接求
逆向求
用数轴
用法则
绝对值为正数的数有2个,它们互为相反数
绝对值为0的数只有1个,是0
含绝对值的加减运算
分类讨论
数形结合
含绝对值的不等式
用数轴分析
|a|+|b|=0的形式
a=0
且b=0
先算绝对值再算加减
1.绝对值的概念
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
2.绝对值的性质
3.去绝对值的法则
(1)|a|≥0
(2)若a和b是互为相反数,则|a|=|b|.
|a|=
a
0
?a
(a>0)
(a=0)
(a<0)
板书设计
作业布置
1.作业本B
1.3绝对值
2.自主练习
https://www.21cnjy.com/help/help_extract.php
1.3绝对值
浙教版
七年级上
旧知温顾
1.什么是数轴?
规定了原点、正方向、单位长度的直线.
三要素
2.什么相反数?
只有符号不同的两个数互为相反数.
特别地,0的相反数是0.
3.在数轴上,表示互为相反数(0除外)的两个点有什么特征?
位于原点的两侧,并且到原点的距离相等.
新知导入
【问题】暑假里,小海和爸爸制定了每天跑2km的健身计划,在一条东西走向的绿道上,小海从起点O向东跑2km到达A处,小海爸爸从起点O向西跑2km到达B处,小海和爸爸都完成训练计划了吗?
起点O
0
1
2
3
?1
?2
?3
东
西
A处
B处
【思考】1.若记向东为正方向,则A处记做_______,B处记做________.
2.在数轴上,A,B两点到原点的距离相同吗?
+2km
?2km
这两个数相同吗?
不同
小海爸爸
起点
小海
正方向:东
单位长度:1km
距离为2
距离为2
表示的意义是什么?
【小结】完成训练计划与跑步方向、路线无关,只考虑路程.
【问题】数轴上,表示?5和5的点到原点的距离分别是____________.
数轴上,表示?2.5和2.5的点到原点的距离分别是____________.
5和5
2.5和2.5
0
1
2
3
4
?1
?2
?3
?4
5
?5
5
5
2.5
2.5
数轴上,你还能找到两个数所表示的点到原点的距离相等吗?
【思考】所表示的点到原点距离相等的两个数具有什么特点?
【小结】互为相反数的两个数在数轴上对应的点到原点的距离相等.
这个距离在我们数学上有个专有名词,
叫绝对值.
新知导入
新知讲解
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
一个数a的绝对值表示为|a|.
0
1
2
3
4
?1
?2
?3
?4
5
?5
5
5
【例如】
|?5|=
5
|5|=
5
【思考】|a|的几何意义是什么?
数
形
结合
|a|的几何意义是数轴上表示数a的点到原点的距离.
例题解析
例1
求下列各数的绝对值:
?1.6,,0,
?10,+10
|?1.6|=
1.6
解
||=
|0|=
0
|?10|=
10
|+10|=
10
【思考】观察上面5个等式
1.从结果看,一个数的绝对值有什么特点?
1.任何数的绝对值都大于或等于0
(即绝对值是非负数)
2.一个数的绝对值与原数有什么关系?
2.正数的绝对值是它本身
负数的绝对值是它的相反数
0的绝对值是0
3.互为相反数的两个数,它们的绝对值有什么关系?
3.互为相反数的两个数的绝对值相等
法则
例题解析
例2
求绝对值等于4的数.
解:
因为数轴上到原点的距离等于4个单位长度的点有两个,即表示+4的点P和表示?4的点M,所以绝对值等于4的数是+4和?4.
几何意义?
0
1
2
3
4
?1
?2
?3
?4
5
?5
4个单位长度
4个单位长度
P
M
方法(一)
方法(二)
因为|+4|=4,|?4|=4,
所以绝对值等于4的数是+4和?4.
课堂练习
1.判断:
(1)一个数的绝对值是
2,则这数是2.
(2)|5|=|?5|.
(3)|?0.3|=|0.3|.
(4)|3|>0.
(5)|?1.4|>0.
(6)有理数的绝对值一定是正数.
(7)若a=b,则|a|=|b|.
(8)若|a|=|b|,则a=b.
(9)若|a|=?a,则a必为负数.
(10)互为相反数的两个数的绝对值相等.
课堂练习
2.计算:
(1)|5?1|=(
).
(2)1+|?5|=(
).
(3)|5|?|?3|=(
).
(4)|?1|
+
|?2|=(
).
(5)|+3|?|?3|=
(
).
4
6
2
3
0
3.下列说法中,正确的是( )
(A)最小的有理数是0
(B)最小的正整数是0
(C)绝对值最小的负数是?1
(D)绝对值最小的有理数是0
D
课堂练习
6.绝对值小于3的整数有_____个,分别是_____________________.
7.绝对值不大于5的整数中,最大的数是_____,最小的数是_____.
4.绝对值等于2的数是_________.
2或?2
5.一个数的绝对值是它本身,那么这个数是__________.
正数或0
(非负数)
5
?2、?1、0、1、2
5
?5
8.如图,图中数轴的单位长度为1.如果点B,C所表示的数的绝对值相
等,那么点A表示的数是________.
?5
拓展提升
1.若|a|+|b|=0
,则a=_____,b=
_____
.
0
0
2.已知|x?2|+|y?1|=0
,则x+y=
_____
.
2
3.计算:|?1|+|?
|+|?
|+…+|?
|
解:原式=++?+…+?
=?
=
课堂总结
绝对值
概念
性质
法则
应用
一个数在数轴上对应的点到原点的距离
符号
|
|
任何数的绝对值都大于或等于0
互为相反数的两个数的绝对值相等
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
直接求
逆向求
用数轴
用法则
绝对值为正数的数有2个,它们互为相反数
绝对值为0的数只有1个,是0
含绝对值的加减运算
分类讨论
数形结合
含绝对值的不等式
用数轴分析
|a|+|b|=0的形式
a=0
且b=0
先算绝对值再算加减
1.绝对值的概念
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
2.绝对值的性质
3.去绝对值的法则
(1)|a|≥0
(2)若a和b是互为相反数,则|a|=|b|.
|a|=
a
0
?a
(a>0)
(a=0)
(a<0)
板书设计
作业布置
1.作业本B
1.3绝对值
2.自主练习
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
