2021-2022学年浙教版数学八年级上册1.1 认识三角形(第1课时)同步课件(共38张PPT)
文档属性
| 名称 | 2021-2022学年浙教版数学八年级上册1.1 认识三角形(第1课时)同步课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 945.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
第1章
三角形的初步认识
第1节
认识三角形
第1课时
三角形的有关概念及三边关系
情景导入
在这座铁塔上我们可以看到许多三角形的支架,你能举出在生活中
看到的三角形的例子吗?
那么,怎样的图形叫做三角形呢?
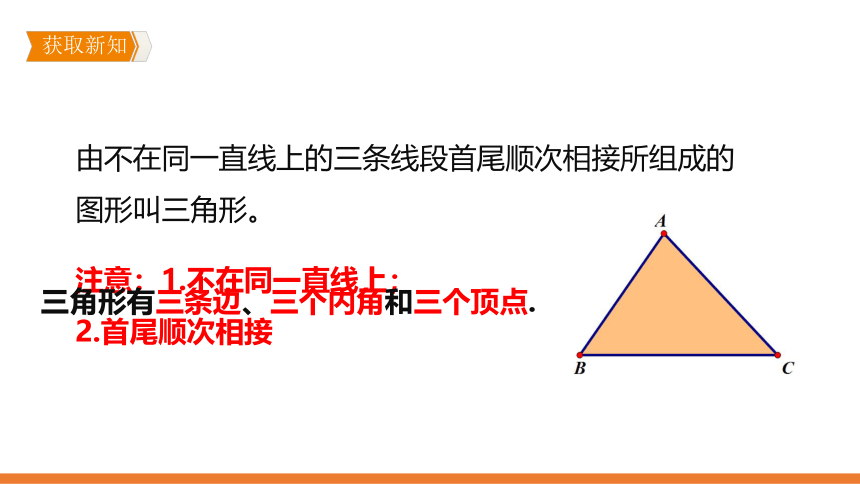
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形。
注意:1.不在同一直线上;
2.首尾顺次相接
三角形有三条边、三个内角和三个顶点.
获取新知
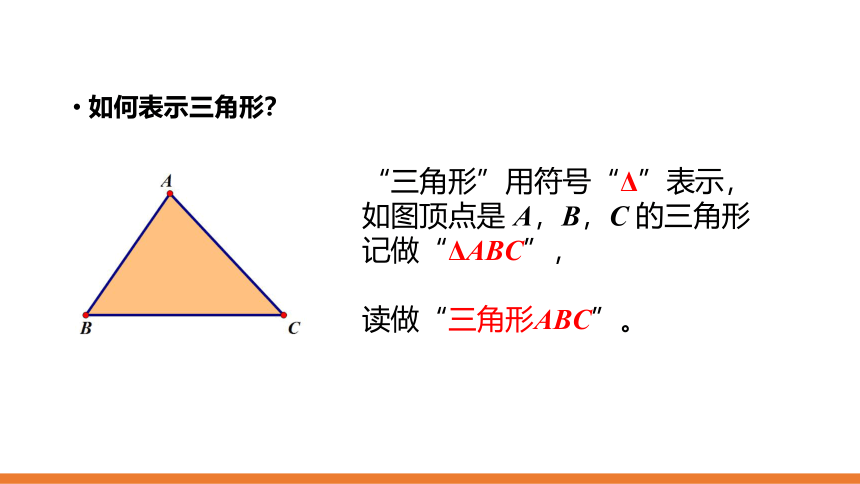
“三角形”用符号“Δ”表示,如图顶点是
A,B,C
的三角形记做“ΔABC”,
读做“三角形ABC”。
如何表示三角形?
BC
、
AC
、AB
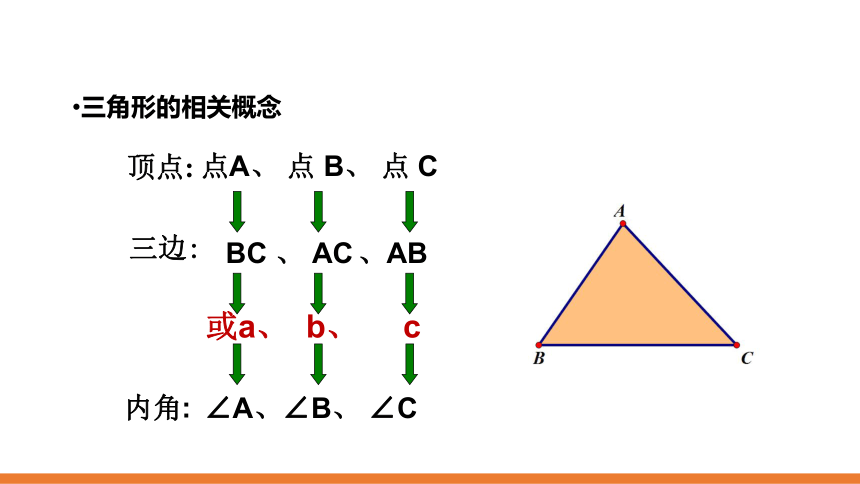
内角:
∠A、∠B、
∠C
点A、
点
B、
点
C
或a、
b、
c
三边:
顶点:
三角形的相关概念
【思考】三角形的三个内角有什么关系?
回顾我们小学做过的剪拼,你是怎样操作的?
把一个三角形的两个角剪下拼在第三个角的顶点处,可得到∠A+∠B+∠ACB=180°.
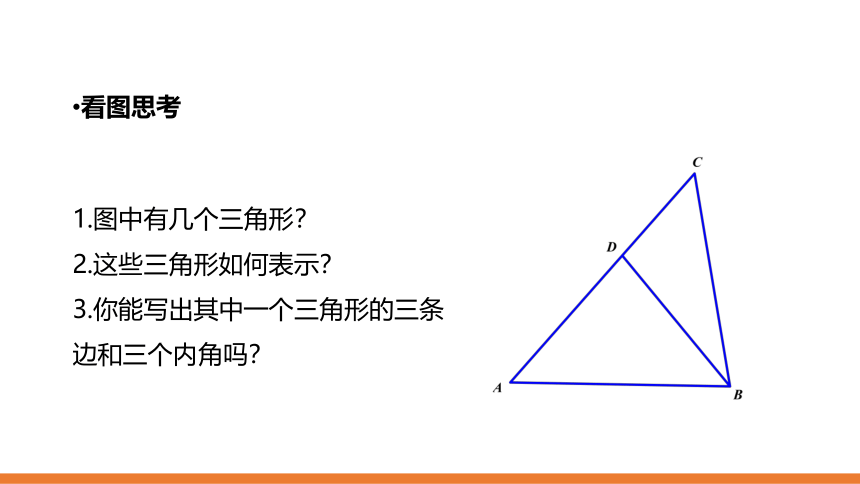
1.图中有几个三角形?
2.这些三角形如何表示?
3.你能写出其中一个三角形的三条边和三个内角吗?
看图思考
【思考】三角形怎样分类?
三
角
形
三个内角都是锐角的三角形是
锐角三角形
有一个内角是直角的三角形是
直角三角形
有一个内角是钝角的三角形是
钝角三角形
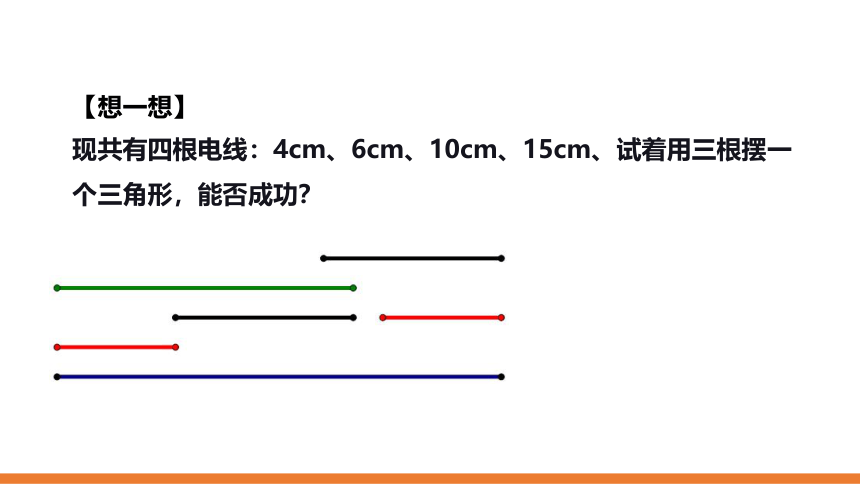
【想一想】
现共有四根电线:4cm、6cm、10cm、15cm、试着用三根摆一个三角形,能否成功?
1
2
3
4
三角形任何两边的和大于第三边.
A
B
C
a
b
c
a+b>c
a+c>b
c+b>a
三角形的性质
【例1】判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1)a=2.5
cm,b=3cm,c=5cm
(2)e=6.3cm,f=6.3cm,g=12.6cm
分析:要判断三条线段能否组成三角形,依据“三角形任何两边的和大于第三边”,只要把最长的一条线段与另外两条线段的和作比较.如果最长的一条线段小于另外两条线段的和,那么这三条线段就能组成三角形如果最长的一条线段大于或等于另外两条线段的和,那么这三条线段就不能组成三角形
例题精讲
【例1】判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1)a=2.5
cm,b=3cm,c=5cm
(2)e=6.3cm,f=6.3cm,g=12.6cm
解(1):最长线段是c=5cm,a+b=2.5+3=5.5(cm)
∴a+b>c,所以线段a,b,c能组成三角形
(2)∵最长线段是g=12.6cm
e+f=6.3+6.3=12.6(cm),
e+f=g,所以线段e,f,g不能组成三角形
想一想
三角形的任意两边之差与第三边有什么关系?
三角形任意两边之差小于第三边.
两边之差<第三边<两边之和
课堂小结
1.三角形内角和定理:
三角形的内角和等于180°。
即:△ABC中,
∠A
+∠B
+∠C=180
°
2.推论:三角形的一个外角等于和它不相邻的两个内角的和。
3.三角形的三边之间的关系
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
1、一个三角形有两边相等,已知其中一边是3cm,另一边是9cm,则这个三角形的周长是________
2.三角形的两边长分别是2和3,若第三边长是奇数,则第三边长为_____;
若第三边长是偶数,则三角形的周长为_____________.
随堂演练
21cm
3cm
7cm或9cm
3.如图,在△BCD中,BC=4,BD=5.
(1)求CD的取范围;
解:∵在△BCD中,BC=4,BD=5,∴1<DC<9.
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
∵AE∥BD,∠BDE=125°,
∴∠AEC=180°-∠BDE=55°,
又∵∠A=55°,∴∠C=180°-55°-55°=70°.
第1章
三角形的初步认识
第1节
认识三角形
第2课时
三角形中的的重要线段
知识回顾
定义
图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
┐
获取新知
角是轴对称图形吗?它的对称轴是什么?
∠1=∠2,角平分线即为对称轴
一、三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
如图,∠BAC的平分线交BC于点D,线段AD就是ΔABC的一条角平分线。
三角形的角平分线定义
A
D
B
C
几何语言
∴∠BAD=∠DAC=
∠BAC
∵AD是△BAC的角平分线
A
B
C
D
注意
三角形的角平分线是一条线段
三角形角平分线的性质
直角三角形
钝角三角形
锐角三角形
三角形的三条角平分线交于同一点.
任意画一个三角形,用刻度尺
画BC的中点D,连接AD。
A
D
C
B
二、三角形的中线
三角形中线的定义
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。
A
D
C
B
如图,D为BC
的中点,线段AD就是△ABC
的BC上的中线。
几何语言
A
D
C
B
∵AD是△BAC的中线
∴BD=DC=
BC
三角形中线的性质
直角三角形
钝角三角形
锐角三角形
三角形的三条中线交于一点,这个交点就是三角形的重心.
三、三角形的高
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高
三角形高的定义
∵
AD
⊥
BC
∴
AD是△
ABC的BC边上的高
A
B
C
D
∵AD是△
ABC的BC边上的高
∴
AD
⊥
BC
A
B
C
E
F
O
A
B
C
D
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
A
B
C
D
E
F
O
AD
三角形高的性质
三角形的三条高所在直线交于一点,
这个交点叫做三角形的垂心.
例题精讲
例1
如图,AE是
△ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
解:∵AE是△ABC的角平分线,
∵
∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE=
∠BAC.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
A
B
C
E
例2
在△ABC中,AB=AC,AC边上的中线BD△ABC的周长分为12
cm和15
cm两部分,求△ABC的各边长.
解:设AB=x
cm,则AD=CD=
x
cm.
(1)如图①,若AB+AD=12
cm,则x+
x=12.解得x=8,
即AB=AC=8
cm,则CD=4
cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8
cm,8
cm,11
cm.
(2)如图②,若AB+AD=15
cm,则x+
x=15.
解得x=10,即AB=AC=10
cm,则CD=5
cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10
cm,10
cm,7
cm.
综上所述,△ABC的三边长分别为8
cm,8
cm,11
cm或10
cm,10
cm,7
cm.
例3
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=80°,∠C=40°,求∠DAE的大小.
∵
AD是△ABC的高,
∴∠ADC=90°.
∵
根据“三角形内角和等于180°”,知∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-∠ADC-∠C
=180°-90°-40°=50°.
解:∵AE是△ABC的角平分线,且∠BAC=80°,
∴∠CAE=
∠BAC=40°,
∴∠DAE=∠DAC-∠CAE=50°-40°=
10°.
B
A
C
D
E
随堂演练
1.小华在电话中问小明:“已知一个三角形的三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )
C
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
3.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
A
4.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
AF
DC
AC
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2______.
∠2
∠4
∠ABC
5.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
6.如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
课堂小结
三角形的
重要线段
概念
图形
表示法
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中的线段
∵
AD是△ABC的BC上的中线.
∴
BD=CD=
BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的∠BAC的平分线
∴
∠1=∠2=
∠BAC
第1章
三角形的初步认识
第1节
认识三角形
第1课时
三角形的有关概念及三边关系
情景导入
在这座铁塔上我们可以看到许多三角形的支架,你能举出在生活中
看到的三角形的例子吗?
那么,怎样的图形叫做三角形呢?
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形。
注意:1.不在同一直线上;
2.首尾顺次相接
三角形有三条边、三个内角和三个顶点.
获取新知
“三角形”用符号“Δ”表示,如图顶点是
A,B,C
的三角形记做“ΔABC”,
读做“三角形ABC”。
如何表示三角形?
BC
、
AC
、AB
内角:
∠A、∠B、
∠C
点A、
点
B、
点
C
或a、
b、
c
三边:
顶点:
三角形的相关概念
【思考】三角形的三个内角有什么关系?
回顾我们小学做过的剪拼,你是怎样操作的?
把一个三角形的两个角剪下拼在第三个角的顶点处,可得到∠A+∠B+∠ACB=180°.
1.图中有几个三角形?
2.这些三角形如何表示?
3.你能写出其中一个三角形的三条边和三个内角吗?
看图思考
【思考】三角形怎样分类?
三
角
形
三个内角都是锐角的三角形是
锐角三角形
有一个内角是直角的三角形是
直角三角形
有一个内角是钝角的三角形是
钝角三角形
【想一想】
现共有四根电线:4cm、6cm、10cm、15cm、试着用三根摆一个三角形,能否成功?
1
2
3
4
三角形任何两边的和大于第三边.
A
B
C
a
b
c
a+b>c
a+c>b
c+b>a
三角形的性质
【例1】判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1)a=2.5
cm,b=3cm,c=5cm
(2)e=6.3cm,f=6.3cm,g=12.6cm
分析:要判断三条线段能否组成三角形,依据“三角形任何两边的和大于第三边”,只要把最长的一条线段与另外两条线段的和作比较.如果最长的一条线段小于另外两条线段的和,那么这三条线段就能组成三角形如果最长的一条线段大于或等于另外两条线段的和,那么这三条线段就不能组成三角形
例题精讲
【例1】判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1)a=2.5
cm,b=3cm,c=5cm
(2)e=6.3cm,f=6.3cm,g=12.6cm
解(1):最长线段是c=5cm,a+b=2.5+3=5.5(cm)
∴a+b>c,所以线段a,b,c能组成三角形
(2)∵最长线段是g=12.6cm
e+f=6.3+6.3=12.6(cm),
e+f=g,所以线段e,f,g不能组成三角形
想一想
三角形的任意两边之差与第三边有什么关系?
三角形任意两边之差小于第三边.
两边之差<第三边<两边之和
课堂小结
1.三角形内角和定理:
三角形的内角和等于180°。
即:△ABC中,
∠A
+∠B
+∠C=180
°
2.推论:三角形的一个外角等于和它不相邻的两个内角的和。
3.三角形的三边之间的关系
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
1、一个三角形有两边相等,已知其中一边是3cm,另一边是9cm,则这个三角形的周长是________
2.三角形的两边长分别是2和3,若第三边长是奇数,则第三边长为_____;
若第三边长是偶数,则三角形的周长为_____________.
随堂演练
21cm
3cm
7cm或9cm
3.如图,在△BCD中,BC=4,BD=5.
(1)求CD的取范围;
解:∵在△BCD中,BC=4,BD=5,∴1<DC<9.
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
∵AE∥BD,∠BDE=125°,
∴∠AEC=180°-∠BDE=55°,
又∵∠A=55°,∴∠C=180°-55°-55°=70°.
第1章
三角形的初步认识
第1节
认识三角形
第2课时
三角形中的的重要线段
知识回顾
定义
图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
┐
获取新知
角是轴对称图形吗?它的对称轴是什么?
∠1=∠2,角平分线即为对称轴
一、三角形的角平分线
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
如图,∠BAC的平分线交BC于点D,线段AD就是ΔABC的一条角平分线。
三角形的角平分线定义
A
D
B
C
几何语言
∴∠BAD=∠DAC=
∠BAC
∵AD是△BAC的角平分线
A
B
C
D
注意
三角形的角平分线是一条线段
三角形角平分线的性质
直角三角形
钝角三角形
锐角三角形
三角形的三条角平分线交于同一点.
任意画一个三角形,用刻度尺
画BC的中点D,连接AD。
A
D
C
B
二、三角形的中线
三角形中线的定义
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。
A
D
C
B
如图,D为BC
的中点,线段AD就是△ABC
的BC上的中线。
几何语言
A
D
C
B
∵AD是△BAC的中线
∴BD=DC=
BC
三角形中线的性质
直角三角形
钝角三角形
锐角三角形
三角形的三条中线交于一点,这个交点就是三角形的重心.
三、三角形的高
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高
三角形高的定义
∵
AD
⊥
BC
∴
AD是△
ABC的BC边上的高
A
B
C
D
∵AD是△
ABC的BC边上的高
∴
AD
⊥
BC
A
B
C
E
F
O
A
B
C
D
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
A
B
C
D
E
F
O
AD
三角形高的性质
三角形的三条高所在直线交于一点,
这个交点叫做三角形的垂心.
例题精讲
例1
如图,AE是
△ABC的角平分线.已知∠B=45°,
∠C=60°,求∠BAE和∠AEB的度数.
解:∵AE是△ABC的角平分线,
∵
∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE=
∠BAC.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
A
B
C
E
例2
在△ABC中,AB=AC,AC边上的中线BD△ABC的周长分为12
cm和15
cm两部分,求△ABC的各边长.
解:设AB=x
cm,则AD=CD=
x
cm.
(1)如图①,若AB+AD=12
cm,则x+
x=12.解得x=8,
即AB=AC=8
cm,则CD=4
cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8
cm,8
cm,11
cm.
(2)如图②,若AB+AD=15
cm,则x+
x=15.
解得x=10,即AB=AC=10
cm,则CD=5
cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10
cm,10
cm,7
cm.
综上所述,△ABC的三边长分别为8
cm,8
cm,11
cm或10
cm,10
cm,7
cm.
例3
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=80°,∠C=40°,求∠DAE的大小.
∵
AD是△ABC的高,
∴∠ADC=90°.
∵
根据“三角形内角和等于180°”,知∠ADC+∠C+∠DAC=180°,
∴
∠DAC=180°-∠ADC-∠C
=180°-90°-40°=50°.
解:∵AE是△ABC的角平分线,且∠BAC=80°,
∴∠CAE=
∠BAC=40°,
∴∠DAE=∠DAC-∠CAE=50°-40°=
10°.
B
A
C
D
E
随堂演练
1.小华在电话中问小明:“已知一个三角形的三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是( )
C
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
3.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
A
4.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
AF
DC
AC
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2______.
∠2
∠4
∠ABC
5.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC
的周长为25cm,求ΔADC的周长.
解:∵CD是△ABC的中线,
∴BD=AD,
∴△DBC的周长=BC+BD+CD=25cm,
则BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
6.如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
课堂小结
三角形的
重要线段
概念
图形
表示法
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中的线段
∵
AD是△ABC的BC上的中线.
∴
BD=CD=
BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的∠BAC的平分线
∴
∠1=∠2=
∠BAC
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
