2021-2022学年九年级数学浙教版上册《1.4二次函数的应用》同步能力提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学浙教版上册《1.4二次函数的应用》同步能力提升训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览



文档简介
2021-2022学年浙教版九年级数学上册《1.4二次函数的应用》同步能力提升训练(附答案)
一.选择题(共10小题)
1.如图,抛物线y1=ax2+bx+c与直线y2=kx+m的交点为A(1,﹣3),B(6,1).当y1>y2时,x的取值范围是( )
A.1<x<6
B.﹣3<x<1
C.x<﹣3或x>1
D.x<1或x>6
2.在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染,则y与x的函数关系式为( )
A.y=2(1+x)2
B.y=(2+x)2
C.y=2+2x2
D.y=(1+2x)2
3.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60
B.65
C.70
D.75
4.飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=60t﹣1.5t2,那么飞机着陆后滑行多长时间才能停下来( )
A.10s
B.20s
C.30s
D.40s
5.已知二次函数y=ax2+bx﹣3(a>0)的图象与x轴的交点A的坐标为(n,0),顶点D的坐标为(m,t),若m+n=0,则t的值为( )
A.﹣7
B.﹣6
C.﹣5
D.﹣4
6.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1
B.2
C.3
D.4
7.已知抛物线y=a(x﹣h)2+k与x轴有两个交点A(﹣1,0),B(3,0),抛物线y=a(x﹣h﹣m)2+k与x轴的一个交点是(4,0),则m的值是( )
A.5
B.﹣1
C.5或1
D.﹣5或﹣1
8.若抛物线y=x2+bx+c与x轴两个交点间的距离为4.对称轴为直线x=2,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )
A.(2,4)
B.(﹣2,4)
C.(﹣2,﹣4)
D.(2,﹣4)
9.关于x的二次函数y=ax2﹣2ax+1(a≠0,a为常数),下列说法错误的是( )
A.函数的对称轴为直线x=1
B.函数必经过点(2,1)
C.当x>1时,y随x的增大而增大
D.当0<a<1时,函数图象与x轴无交点
10.如图是二次函数y=x2+bx+c的部分图象,抛物线的对称轴为直线x=1,与x轴交于点A(﹣1,0),与y轴交于点B.给出下列结论:
①b=c;②点B的坐标为(0,﹣3);③抛物线与x轴另一个交点的坐标为(3,0);
④抛物线的顶点坐标为(1,﹣4);⑤函数最大值为﹣4.
其中正确的个数为( )
A.5
B.4
C.3
D.2
二.填空题(共8小题)
11.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),则方程ax2+bx+c=0(a≠0)的两根是
.
12.已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C,点D(4,y)在抛物线上,E是该抛物线对称轴上一动点,当BE+DE的值最小时,△ACE的面积为
.
13.如图,抛物线y=﹣x2﹣x+与x轴相交于点A,B,与y轴相交于点C,则△ABC的面积为
.
14.某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是
元.
15.如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为
米.
16.已知函数y=(a﹣1)x2﹣2ax+a﹣3的图象与两坐标轴共有两个交点,则a的值为
.
17.某宾馆有50个房间供游客居住.当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有1个房间空闲.如果游客居住房间,宾馆需要对每个房间每天支出40元的各种费用.房价定为
元时,宾馆利润最大,最大利润是
元.
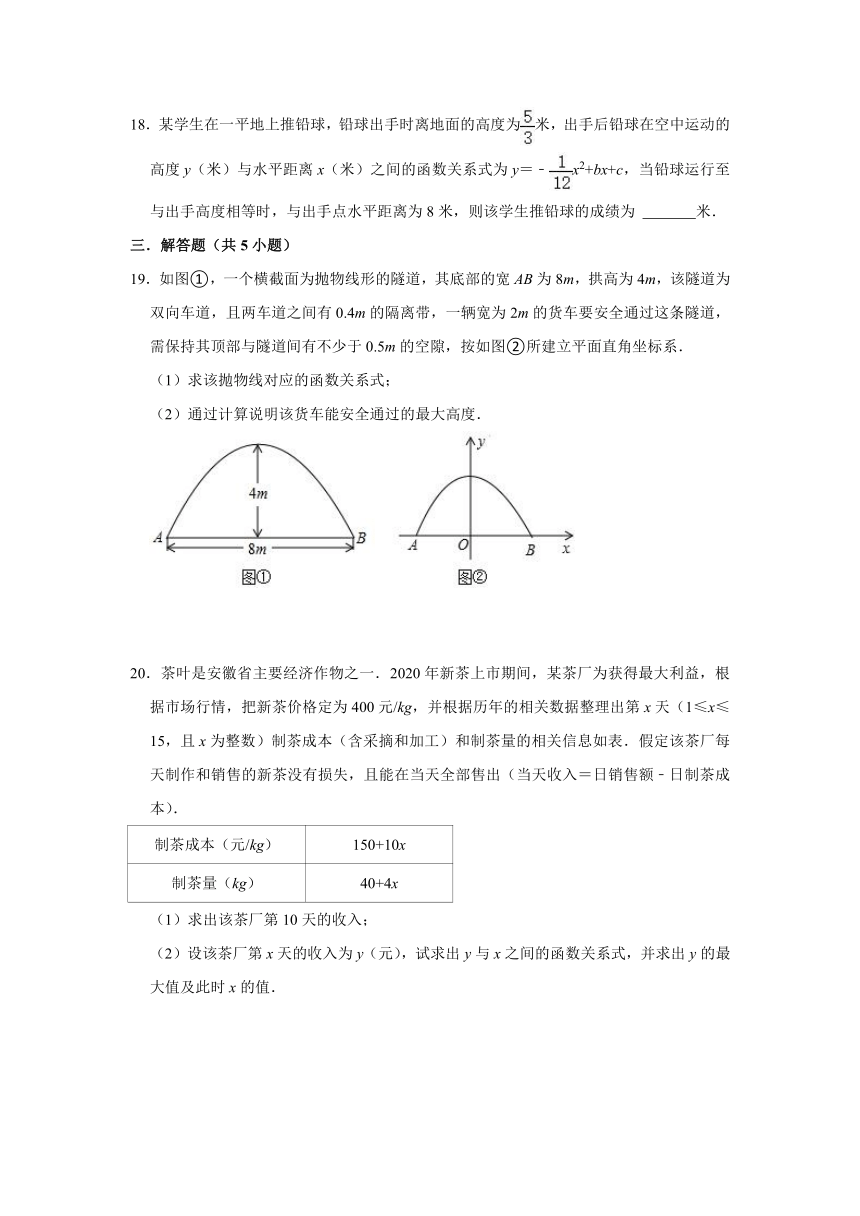
18.某学生在一平地上推铅球,铅球出手时离地面的高度为米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为y=﹣x2+bx+c,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为
米.
三.解答题(共5小题)
19.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8m,拱高为4m,该隧道为双向车道,且两车道之间有0.4m的隔离带,一辆宽为2m的货车要安全通过这条隧道,需保持其顶部与隧道间有不少于0.5m的空隙,按如图②所建立平面直角坐标系.
(1)求该抛物线对应的函数关系式;
(2)通过计算说明该货车能安全通过的最大高度.
20.茶叶是安徽省主要经济作物之一.2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额﹣日制茶成本).
制茶成本(元/kg)
150+10x
制茶量(kg)
40+4x
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元),试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
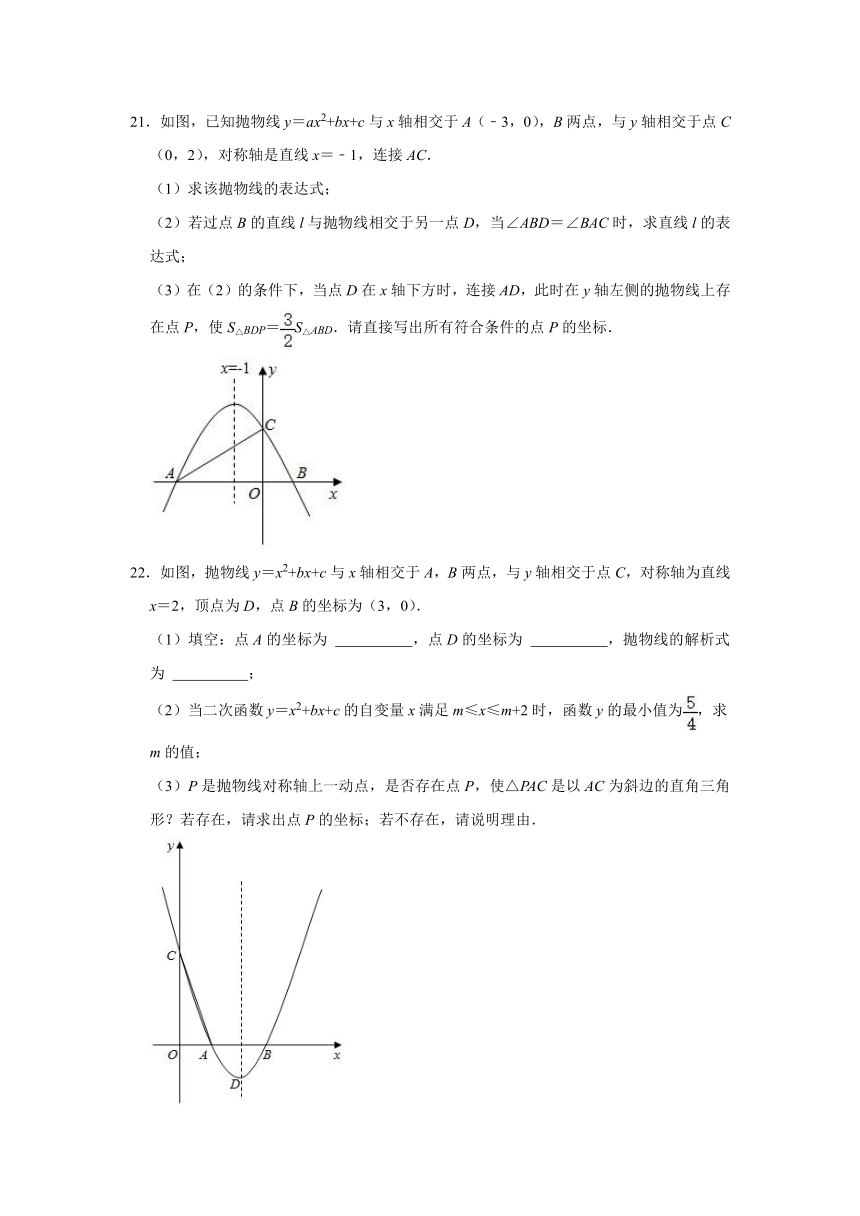
21.如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=﹣1,连接AC.
(1)求该抛物线的表达式;
(2)若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;
(3)在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使S△BDP=S△ABD.请直接写出所有符合条件的点P的坐标.
22.如图,抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,顶点为D,点B的坐标为(3,0).
(1)填空:点A的坐标为
,点D的坐标为
,抛物线的解析式为
;
(2)当二次函数y=x2+bx+c的自变量x满足m≤x≤m+2时,函数y的最小值为,求m的值;
(3)P是抛物线对称轴上一动点,是否存在点P,使△PAC是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
23.如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式;
(2)连接BC,求直线BC的解析式;
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值;
(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题)
1.解:∵二次函数y1=ax2+bx+c与一次函数y2=kx+m的交点A、B的坐标分别为(1,﹣3)、(6,1),
∴当y1>y2时,x的取值范围是x<1或x>6,
故选:D.
2.解:根据题意可得,y与x的函数关系式为:y=2+2x+(2+2x)x=2(1+x)2.
故选:A.
3.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
4.解:∵a=﹣1.5<0,
∴函数有最大值,
当t=﹣=﹣=20(秒),
即飞机着陆后滑行20秒能停下来,
故选:B.
5.解:∵二次函数y=ax2+bx﹣3(a>0)的图象与x轴的交点A的坐标为(n,0),顶点D的坐标为(m,t),m+n=0,
∴m=﹣n=,
∴a?()2+b?﹣3=0,
解得=1,
∴t===﹣3﹣=﹣3﹣1=﹣4,
故选:D.
6.解:如图所示,
过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,
则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),
∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA?AD=1×2=2.
故选:B.
7.解:∵抛物线y=a(x﹣h)2+k的对称轴为直线x=h,抛物线y=a(x﹣h﹣m)2+k的对称轴为直线x=h+m,
∴当点A(﹣1,0)平移后的对应点为(4,0),则m=4﹣(﹣1)=5;
当点B(3,0)平移后的对应点为(4,0),则m=4﹣3=1,
即m的值为5或1.
故选:C.
8.解:设抛物线y=x2+bx+c与x轴两个交点坐标为(x1,0),(x2,0),
∵抛物线y=x2+bx+c与x轴两个交点间的距离为4.对称轴为直线x=2,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=16,﹣=2,
∴(﹣)2﹣4×=16,b=﹣4,
解得c=0,
∴抛物线的解析式为y=x2﹣4x=(x﹣2)2﹣4,
∴顶点P的坐标为(2,﹣4),
∴点P关于x轴的对称点的坐标是(2,4),
故选:A.
9.解:∵二次函数y=ax2﹣2ax+1=a(x﹣1)2﹣a+1(a≠0,a为常数),
∴该函数的对称轴为直线x=1,故选项A不符合题意;
当x=2时,y=1,故选项B不符合题意;
a的正负不知道,故当x>1时,y随x的增大如何变化无法确定,故选项C符合题意;
当0<a<1时,该函数图象开口向上,Δ=(﹣2a)2﹣4a×1=(2a﹣1)2﹣1<0,则当0<a<1时,函数图象与x轴无交点,故故选项D不符合题意;
故选:C.
10.解:∵二次函数y=x2+bx+c的对称轴为直线x=1,与x轴交于点A(﹣1,0),
∴,抛物线与x轴另一个交点的坐标为(3,0),故③正确,符合题意;
解得,
∴b≠c,故①错误,不符合题意;
函数解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴点B的坐标为(0,﹣3),故②正确,符合题意;
抛物线的顶点坐标为(1,﹣4),故④正确,符合题意;
函数图象开口向上,当x=1时,取得最小值﹣4,故⑤错误,不符合题意;
故选:C.
二.填空题(共8小题)
11.解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),
∴抛物线与x轴的另一个交点为(﹣1,0),
∴当y=0时,0=ax2+bx+c的两个根为x=3或x=﹣1.
故答案为:x=3或x=﹣1.
12.解:当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
抛物线的对称轴为直线x=1,
当x=0时,y=x2﹣2x﹣3=﹣3,则C(0,﹣3),
当x=4时,y=x2﹣2x﹣3=5,则D(4,5),
连接AD交直线x=1于E,交y轴于F点,如图,
∵BE+DE=EA+DE=AD,
∴此时BE+DE的值最小,
设直线AD的解析式为y=kx+b,
把A(﹣1,0),D(4,5)代入得,解得,
∴直线AD的解析式为y=x+1,
当x=1时,y=x+1=2,则E(1,2),
当x=0时,y=x+1=1,则F(0,1),
∴S△ACE=S△ACF+S△ECF=×4×1+×4×1=4.
故答案为4.
13.解:∵抛物线y=﹣x2﹣x+,
∴当y=0时,x1=﹣3,x2=1,当x=0时,y=,
∴点A的坐标为(﹣3,0),点B的坐标为(1,0),点C的坐标为(0,),
∴AB=1﹣(﹣3)=1+3=4,OC=,
∴△ABC的面积为:=3,
故答案为:3.
14.解:设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐提高b元,则每天卖出(80﹣2b)份,
由题意可得,40+2a+80﹣2b=40+80,
解a=b,
∴总利润W=(12﹣a)(40+2a)+(8+a)(80﹣2a)
=﹣4a2+48a+1120
=﹣4(a﹣6)2+1264,
∵﹣4<0,
∴当a=6时,W取得最大值1264,
即两种快餐一天的总利润最多为1264元.
故答案为:1264.
15.解:∵跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.
∴抛物线的对称轴为x=2.5,
∴x=﹣=2.5,解得:b=3,
∴抛物线为y=﹣x2+3x+1,
∵人梯到起跳点A的水平距离是4,
∴点B的横坐标为4,
则yB=﹣×42+3×4+1=3.4,即BC=3.4米.
故答案为:3.4.
16.解:当a﹣1=0时,即a=1,函数为y=﹣2x﹣2,此一次函数与坐标轴共有两个交点;
当a﹣1≠0,此函数为二次函数,
若a﹣3=0,抛物线解析式为y=2x2﹣6x,抛物线经过原点且抛物线与x轴有两个交点;
若△=0,抛物线的顶点在x轴上,即△=(﹣2a)2﹣4(a﹣1)(a﹣3)=0,解得a=,抛物线解析式为y=﹣x2﹣x﹣=﹣(x+3)2,抛物线的顶点为(﹣3,0),则抛物线与两坐标轴共有两个交点.
综上所述,a的值为1或3或.
故答案为1或3或.
17.解:设空闲房间为x个,则定价增加了10x元,设宾馆的利润为y元,由题意得:
y=(180+10x﹣40)(50﹣x)
=﹣10x2+360x+7000
=﹣10(x﹣18)2+10240,
∵a=﹣10<0,抛物线开口向下,
∴当x=18时,y有最大值,为10240.
此时房间定价为180+10×18=360(元).
∴房间定价为360元时,利润最大,最大利润为10240元.
故答案为:360,10240.
18.解:设铅球出手点为点A,当铅球运行至与出手高度相等时为点B,根据题意建立平面直角坐标系,如图:
由题意可知,点A(0,),点B(8,),代入y=﹣x2+bx+c,得:
,
解得.
∴y=﹣x2+x+,
当y=0时,0=﹣x2+x+,
解得x1=10,x2=﹣2(不符合题意,舍去).
∴该学生推铅球的成绩为10m.
故答案为:10.
三.解答题(共5小题)
19.解:(1)如图②中,A(4,0),C(0,4),
设抛物线解析式为y=ax2+k,
由题意,得,
解得:,
∴抛物线表达式为.
(2)2+=2.2,
当x=2.2时,y=﹣×2.22+4=2.79,
当y=2.79时,2.79﹣0.5=2.29
(m).
答:该货车能够通行的最大高度为2.29
m.
20.解:(1)当x=10时,制茶成本为:150+10x=150+10×10=250(元/千克);
制茶量为:40+4x=40+4×10=80(kg);
该茶厂第10天的收入为:(400﹣250)×80=12000(元).
∴该茶厂第10天的收入为12000元;
(2)根据题意得:
y=[400﹣(150+10x)]?(40+4x)
=﹣40x2+600x+10000
=﹣40(x﹣7.5)2+12250,
∵a=﹣40<0,1≤x≤15,且x是正整数,
∴x=7或8时,y取得最大值12240元.
∴y与x之间的函数关系式为y=﹣40x2+600x+10000,x=7或8时,y取得最大值12240元.
21.解:(1)∵抛物线的对称轴为x=﹣1,
∴﹣=﹣1,
∴b=2a,
∵点C的坐标为(0,2),
∴c=2,
∴抛物线的解析式为y=ax2+2ax+2,
∵点A(﹣3,0)在抛物线上,
∴9a﹣6a+2=0,
∴a=﹣,
∴b=2a=﹣,
∴抛物线的解析式为y=﹣x2﹣x+2;
(2)Ⅰ、当点D在x轴上方时,如图1,
记BD与AC的交点为点E,
∵∠ABD=∠BAC,
∴AE=BE,
∵直线x=﹣1垂直平分AB,
∴点E在直线x=﹣1上,
∵点A(﹣3,0),C(0,2),
∴直线AC的解析式为y=x+2,
当x=﹣1时,y=,
∴点E(﹣1,),
∵点A(﹣3,0)点B关于x=﹣1对称,
∴B(1,0),
∴直线BD的解析式为y=﹣x+,
即直线l的解析式为y=﹣x+;
Ⅱ、当点D在x轴下方时,如图2,
∵∠ABD=∠BAC,
∴BD∥AC,
由Ⅰ知,直线AC的解析式为y=x+2,
∴直线BD的解析式为y=x﹣,
即直线l的解析式为y=x﹣;
综上,直线l的解析式为y=﹣x+或y=x﹣;
(3)由(2)知,直线BD的解析式为y=x﹣①,
∵抛物线的解析式为y=﹣x2﹣x+2②,
∴或,
∴D(﹣4,﹣),
∴S△ABD=AB?|yD|=×4×=,
∵S△BDP=S△ABD,
∴S△BDP=×=10,
∵点P在y轴左侧的抛物线上,
∴设P(m,﹣m2﹣m+2)(m<0),
过P作y轴的平行线交直线BD于F,
∴F(m,m﹣),
∴PF=|﹣m2﹣m+2﹣(m﹣)|=|m2+2m﹣|,
∴S△BDP=PF?(xB﹣xD)=×|m2+2m﹣|×5=10,
∴m=﹣5或m=2(舍)或m=﹣1或m=﹣2,
∴P(﹣5,﹣8)或(﹣1,)或(﹣2,2).
22.解:(1)∵对称轴为直线x=2,
∴b=﹣4,
∴y=x2﹣4x+c,
∵点B(3,0)是抛物线与x轴的交点,
∴9﹣12+c=0,
∴c=3,
∴y=x2﹣4x+3,
令y=0,x2﹣4x+3=0,
∴x=3或x=1,
∴A(1,0),
∵D是抛物线的顶点,
∴D(2,﹣1),
故答案为(1,0),(2,﹣1),y=x2﹣4x+3;
(2)当m+2<2时,即m<0,
此时当x=m+2时,y有最小值,
则(m+2)2﹣4(m+2)+3=,
解得m=,
∴m=﹣;
当m>2时,此时当x=m时,y有最小值,
则m2﹣4m+3=,
解得m=或m=,
∴m=;
当0≤m≤2时,此时当x=2时,y有最小值为﹣1,与题意不符;
综上所述:m的值为或﹣;
(3)存在,理由如下:
A(1,0),C(0,3),
∴AC=,AC的中点为E(,),
设P(2,t),
∵△PAC是以AC为斜边的直角三角形,
∴PE=AC,
∴=,
∴t=2或t=1,
∴P(2,2)或P(2,1),
∴使△PAC是以AC为斜边的直角三角形时,P点坐标为(2,2)或(2,1).
23.解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,
解得,
∴y=﹣x2+3x+4;
(2)在y=﹣x2+3x+4中,令x=0,则y=4,
∴C(0,4),
设BC的解析式为y=kx+b,
∵B(4,0),C(0,4),
∴,
∴,
∴直线BC的解析式为y=﹣x+4.
(3)如图1中,
由题意A,B关于抛物线的对称轴直线x=对称,
连接BC交直线x=于点P,连接PA,此时PA+PC的值最小,最小值为线段BC的长==4,
此时P(,).
(4)如图2中,存在.
观察图象可知,满足条件的点N的纵坐标为4或﹣4,
对于抛物线y=﹣x2+3x+4,当y=4时,x2﹣3x=0,解得x=0或3,
∴N1(3,4).
当y=﹣4时,x2﹣3x﹣8=0,解得x=,
∴N2(,﹣4),N3(,﹣4),
综上所述,满足条件的点N的坐标为(3,4)或(,﹣4)或(,﹣4).
一.选择题(共10小题)
1.如图,抛物线y1=ax2+bx+c与直线y2=kx+m的交点为A(1,﹣3),B(6,1).当y1>y2时,x的取值范围是( )
A.1<x<6
B.﹣3<x<1
C.x<﹣3或x>1
D.x<1或x>6
2.在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染,则y与x的函数关系式为( )
A.y=2(1+x)2
B.y=(2+x)2
C.y=2+2x2
D.y=(1+2x)2
3.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60
B.65
C.70
D.75
4.飞机着陆后滑行的距离s(单位:m)与滑行的时间t(单位:s)的函数解析式是s=60t﹣1.5t2,那么飞机着陆后滑行多长时间才能停下来( )
A.10s
B.20s
C.30s
D.40s
5.已知二次函数y=ax2+bx﹣3(a>0)的图象与x轴的交点A的坐标为(n,0),顶点D的坐标为(m,t),若m+n=0,则t的值为( )
A.﹣7
B.﹣6
C.﹣5
D.﹣4
6.如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为( )
A.1
B.2
C.3
D.4
7.已知抛物线y=a(x﹣h)2+k与x轴有两个交点A(﹣1,0),B(3,0),抛物线y=a(x﹣h﹣m)2+k与x轴的一个交点是(4,0),则m的值是( )
A.5
B.﹣1
C.5或1
D.﹣5或﹣1
8.若抛物线y=x2+bx+c与x轴两个交点间的距离为4.对称轴为直线x=2,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )
A.(2,4)
B.(﹣2,4)
C.(﹣2,﹣4)
D.(2,﹣4)
9.关于x的二次函数y=ax2﹣2ax+1(a≠0,a为常数),下列说法错误的是( )
A.函数的对称轴为直线x=1
B.函数必经过点(2,1)
C.当x>1时,y随x的增大而增大
D.当0<a<1时,函数图象与x轴无交点
10.如图是二次函数y=x2+bx+c的部分图象,抛物线的对称轴为直线x=1,与x轴交于点A(﹣1,0),与y轴交于点B.给出下列结论:
①b=c;②点B的坐标为(0,﹣3);③抛物线与x轴另一个交点的坐标为(3,0);
④抛物线的顶点坐标为(1,﹣4);⑤函数最大值为﹣4.
其中正确的个数为( )
A.5
B.4
C.3
D.2
二.填空题(共8小题)
11.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),则方程ax2+bx+c=0(a≠0)的两根是
.
12.已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C,点D(4,y)在抛物线上,E是该抛物线对称轴上一动点,当BE+DE的值最小时,△ACE的面积为
.
13.如图,抛物线y=﹣x2﹣x+与x轴相交于点A,B,与y轴相交于点C,则△ABC的面积为
.
14.某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是
元.
15.如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为
米.
16.已知函数y=(a﹣1)x2﹣2ax+a﹣3的图象与两坐标轴共有两个交点,则a的值为
.
17.某宾馆有50个房间供游客居住.当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有1个房间空闲.如果游客居住房间,宾馆需要对每个房间每天支出40元的各种费用.房价定为
元时,宾馆利润最大,最大利润是
元.
18.某学生在一平地上推铅球,铅球出手时离地面的高度为米,出手后铅球在空中运动的高度y(米)与水平距离x(米)之间的函数关系式为y=﹣x2+bx+c,当铅球运行至与出手高度相等时,与出手点水平距离为8米,则该学生推铅球的成绩为
米.
三.解答题(共5小题)
19.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8m,拱高为4m,该隧道为双向车道,且两车道之间有0.4m的隔离带,一辆宽为2m的货车要安全通过这条隧道,需保持其顶部与隧道间有不少于0.5m的空隙,按如图②所建立平面直角坐标系.
(1)求该抛物线对应的函数关系式;
(2)通过计算说明该货车能安全通过的最大高度.
20.茶叶是安徽省主要经济作物之一.2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额﹣日制茶成本).
制茶成本(元/kg)
150+10x
制茶量(kg)
40+4x
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元),试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
21.如图,已知抛物线y=ax2+bx+c与x轴相交于A(﹣3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=﹣1,连接AC.
(1)求该抛物线的表达式;
(2)若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;
(3)在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使S△BDP=S△ABD.请直接写出所有符合条件的点P的坐标.
22.如图,抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,顶点为D,点B的坐标为(3,0).
(1)填空:点A的坐标为
,点D的坐标为
,抛物线的解析式为
;
(2)当二次函数y=x2+bx+c的自变量x满足m≤x≤m+2时,函数y的最小值为,求m的值;
(3)P是抛物线对称轴上一动点,是否存在点P,使△PAC是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
23.如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式;
(2)连接BC,求直线BC的解析式;
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值;
(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案
一.选择题(共10小题)
1.解:∵二次函数y1=ax2+bx+c与一次函数y2=kx+m的交点A、B的坐标分别为(1,﹣3)、(6,1),
∴当y1>y2时,x的取值范围是x<1或x>6,
故选:D.
2.解:根据题意可得,y与x的函数关系式为:y=2+2x+(2+2x)x=2(1+x)2.
故选:A.
3.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
4.解:∵a=﹣1.5<0,
∴函数有最大值,
当t=﹣=﹣=20(秒),
即飞机着陆后滑行20秒能停下来,
故选:B.
5.解:∵二次函数y=ax2+bx﹣3(a>0)的图象与x轴的交点A的坐标为(n,0),顶点D的坐标为(m,t),m+n=0,
∴m=﹣n=,
∴a?()2+b?﹣3=0,
解得=1,
∴t===﹣3﹣=﹣3﹣1=﹣4,
故选:D.
6.解:如图所示,
过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,
则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),
∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
根据平移的性质及抛物线的对称性得到阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA?AD=1×2=2.
故选:B.
7.解:∵抛物线y=a(x﹣h)2+k的对称轴为直线x=h,抛物线y=a(x﹣h﹣m)2+k的对称轴为直线x=h+m,
∴当点A(﹣1,0)平移后的对应点为(4,0),则m=4﹣(﹣1)=5;
当点B(3,0)平移后的对应点为(4,0),则m=4﹣3=1,
即m的值为5或1.
故选:C.
8.解:设抛物线y=x2+bx+c与x轴两个交点坐标为(x1,0),(x2,0),
∵抛物线y=x2+bx+c与x轴两个交点间的距离为4.对称轴为直线x=2,
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=16,﹣=2,
∴(﹣)2﹣4×=16,b=﹣4,
解得c=0,
∴抛物线的解析式为y=x2﹣4x=(x﹣2)2﹣4,
∴顶点P的坐标为(2,﹣4),
∴点P关于x轴的对称点的坐标是(2,4),
故选:A.
9.解:∵二次函数y=ax2﹣2ax+1=a(x﹣1)2﹣a+1(a≠0,a为常数),
∴该函数的对称轴为直线x=1,故选项A不符合题意;
当x=2时,y=1,故选项B不符合题意;
a的正负不知道,故当x>1时,y随x的增大如何变化无法确定,故选项C符合题意;
当0<a<1时,该函数图象开口向上,Δ=(﹣2a)2﹣4a×1=(2a﹣1)2﹣1<0,则当0<a<1时,函数图象与x轴无交点,故故选项D不符合题意;
故选:C.
10.解:∵二次函数y=x2+bx+c的对称轴为直线x=1,与x轴交于点A(﹣1,0),
∴,抛物线与x轴另一个交点的坐标为(3,0),故③正确,符合题意;
解得,
∴b≠c,故①错误,不符合题意;
函数解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴点B的坐标为(0,﹣3),故②正确,符合题意;
抛物线的顶点坐标为(1,﹣4),故④正确,符合题意;
函数图象开口向上,当x=1时,取得最小值﹣4,故⑤错误,不符合题意;
故选:C.
二.填空题(共8小题)
11.解:∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与x轴的一个交点是(3,0),
∴抛物线与x轴的另一个交点为(﹣1,0),
∴当y=0时,0=ax2+bx+c的两个根为x=3或x=﹣1.
故答案为:x=3或x=﹣1.
12.解:当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
抛物线的对称轴为直线x=1,
当x=0时,y=x2﹣2x﹣3=﹣3,则C(0,﹣3),
当x=4时,y=x2﹣2x﹣3=5,则D(4,5),
连接AD交直线x=1于E,交y轴于F点,如图,
∵BE+DE=EA+DE=AD,
∴此时BE+DE的值最小,
设直线AD的解析式为y=kx+b,
把A(﹣1,0),D(4,5)代入得,解得,
∴直线AD的解析式为y=x+1,
当x=1时,y=x+1=2,则E(1,2),
当x=0时,y=x+1=1,则F(0,1),
∴S△ACE=S△ACF+S△ECF=×4×1+×4×1=4.
故答案为4.
13.解:∵抛物线y=﹣x2﹣x+,
∴当y=0时,x1=﹣3,x2=1,当x=0时,y=,
∴点A的坐标为(﹣3,0),点B的坐标为(1,0),点C的坐标为(0,),
∴AB=1﹣(﹣3)=1+3=4,OC=,
∴△ABC的面积为:=3,
故答案为:3.
14.解:设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐提高b元,则每天卖出(80﹣2b)份,
由题意可得,40+2a+80﹣2b=40+80,
解a=b,
∴总利润W=(12﹣a)(40+2a)+(8+a)(80﹣2a)
=﹣4a2+48a+1120
=﹣4(a﹣6)2+1264,
∵﹣4<0,
∴当a=6时,W取得最大值1264,
即两种快餐一天的总利润最多为1264元.
故答案为:1264.
15.解:∵跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.
∴抛物线的对称轴为x=2.5,
∴x=﹣=2.5,解得:b=3,
∴抛物线为y=﹣x2+3x+1,
∵人梯到起跳点A的水平距离是4,
∴点B的横坐标为4,
则yB=﹣×42+3×4+1=3.4,即BC=3.4米.
故答案为:3.4.
16.解:当a﹣1=0时,即a=1,函数为y=﹣2x﹣2,此一次函数与坐标轴共有两个交点;
当a﹣1≠0,此函数为二次函数,
若a﹣3=0,抛物线解析式为y=2x2﹣6x,抛物线经过原点且抛物线与x轴有两个交点;
若△=0,抛物线的顶点在x轴上,即△=(﹣2a)2﹣4(a﹣1)(a﹣3)=0,解得a=,抛物线解析式为y=﹣x2﹣x﹣=﹣(x+3)2,抛物线的顶点为(﹣3,0),则抛物线与两坐标轴共有两个交点.
综上所述,a的值为1或3或.
故答案为1或3或.
17.解:设空闲房间为x个,则定价增加了10x元,设宾馆的利润为y元,由题意得:
y=(180+10x﹣40)(50﹣x)
=﹣10x2+360x+7000
=﹣10(x﹣18)2+10240,
∵a=﹣10<0,抛物线开口向下,
∴当x=18时,y有最大值,为10240.
此时房间定价为180+10×18=360(元).
∴房间定价为360元时,利润最大,最大利润为10240元.
故答案为:360,10240.
18.解:设铅球出手点为点A,当铅球运行至与出手高度相等时为点B,根据题意建立平面直角坐标系,如图:
由题意可知,点A(0,),点B(8,),代入y=﹣x2+bx+c,得:
,
解得.
∴y=﹣x2+x+,
当y=0时,0=﹣x2+x+,
解得x1=10,x2=﹣2(不符合题意,舍去).
∴该学生推铅球的成绩为10m.
故答案为:10.
三.解答题(共5小题)
19.解:(1)如图②中,A(4,0),C(0,4),
设抛物线解析式为y=ax2+k,
由题意,得,
解得:,
∴抛物线表达式为.
(2)2+=2.2,
当x=2.2时,y=﹣×2.22+4=2.79,
当y=2.79时,2.79﹣0.5=2.29
(m).
答:该货车能够通行的最大高度为2.29
m.
20.解:(1)当x=10时,制茶成本为:150+10x=150+10×10=250(元/千克);
制茶量为:40+4x=40+4×10=80(kg);
该茶厂第10天的收入为:(400﹣250)×80=12000(元).
∴该茶厂第10天的收入为12000元;
(2)根据题意得:
y=[400﹣(150+10x)]?(40+4x)
=﹣40x2+600x+10000
=﹣40(x﹣7.5)2+12250,
∵a=﹣40<0,1≤x≤15,且x是正整数,
∴x=7或8时,y取得最大值12240元.
∴y与x之间的函数关系式为y=﹣40x2+600x+10000,x=7或8时,y取得最大值12240元.
21.解:(1)∵抛物线的对称轴为x=﹣1,
∴﹣=﹣1,
∴b=2a,
∵点C的坐标为(0,2),
∴c=2,
∴抛物线的解析式为y=ax2+2ax+2,
∵点A(﹣3,0)在抛物线上,
∴9a﹣6a+2=0,
∴a=﹣,
∴b=2a=﹣,
∴抛物线的解析式为y=﹣x2﹣x+2;
(2)Ⅰ、当点D在x轴上方时,如图1,
记BD与AC的交点为点E,
∵∠ABD=∠BAC,
∴AE=BE,
∵直线x=﹣1垂直平分AB,
∴点E在直线x=﹣1上,
∵点A(﹣3,0),C(0,2),
∴直线AC的解析式为y=x+2,
当x=﹣1时,y=,
∴点E(﹣1,),
∵点A(﹣3,0)点B关于x=﹣1对称,
∴B(1,0),
∴直线BD的解析式为y=﹣x+,
即直线l的解析式为y=﹣x+;
Ⅱ、当点D在x轴下方时,如图2,
∵∠ABD=∠BAC,
∴BD∥AC,
由Ⅰ知,直线AC的解析式为y=x+2,
∴直线BD的解析式为y=x﹣,
即直线l的解析式为y=x﹣;
综上,直线l的解析式为y=﹣x+或y=x﹣;
(3)由(2)知,直线BD的解析式为y=x﹣①,
∵抛物线的解析式为y=﹣x2﹣x+2②,
∴或,
∴D(﹣4,﹣),
∴S△ABD=AB?|yD|=×4×=,
∵S△BDP=S△ABD,
∴S△BDP=×=10,
∵点P在y轴左侧的抛物线上,
∴设P(m,﹣m2﹣m+2)(m<0),
过P作y轴的平行线交直线BD于F,
∴F(m,m﹣),
∴PF=|﹣m2﹣m+2﹣(m﹣)|=|m2+2m﹣|,
∴S△BDP=PF?(xB﹣xD)=×|m2+2m﹣|×5=10,
∴m=﹣5或m=2(舍)或m=﹣1或m=﹣2,
∴P(﹣5,﹣8)或(﹣1,)或(﹣2,2).
22.解:(1)∵对称轴为直线x=2,
∴b=﹣4,
∴y=x2﹣4x+c,
∵点B(3,0)是抛物线与x轴的交点,
∴9﹣12+c=0,
∴c=3,
∴y=x2﹣4x+3,
令y=0,x2﹣4x+3=0,
∴x=3或x=1,
∴A(1,0),
∵D是抛物线的顶点,
∴D(2,﹣1),
故答案为(1,0),(2,﹣1),y=x2﹣4x+3;
(2)当m+2<2时,即m<0,
此时当x=m+2时,y有最小值,
则(m+2)2﹣4(m+2)+3=,
解得m=,
∴m=﹣;
当m>2时,此时当x=m时,y有最小值,
则m2﹣4m+3=,
解得m=或m=,
∴m=;
当0≤m≤2时,此时当x=2时,y有最小值为﹣1,与题意不符;
综上所述:m的值为或﹣;
(3)存在,理由如下:
A(1,0),C(0,3),
∴AC=,AC的中点为E(,),
设P(2,t),
∵△PAC是以AC为斜边的直角三角形,
∴PE=AC,
∴=,
∴t=2或t=1,
∴P(2,2)或P(2,1),
∴使△PAC是以AC为斜边的直角三角形时,P点坐标为(2,2)或(2,1).
23.解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,
解得,
∴y=﹣x2+3x+4;
(2)在y=﹣x2+3x+4中,令x=0,则y=4,
∴C(0,4),
设BC的解析式为y=kx+b,
∵B(4,0),C(0,4),
∴,
∴,
∴直线BC的解析式为y=﹣x+4.
(3)如图1中,
由题意A,B关于抛物线的对称轴直线x=对称,
连接BC交直线x=于点P,连接PA,此时PA+PC的值最小,最小值为线段BC的长==4,
此时P(,).
(4)如图2中,存在.
观察图象可知,满足条件的点N的纵坐标为4或﹣4,
对于抛物线y=﹣x2+3x+4,当y=4时,x2﹣3x=0,解得x=0或3,
∴N1(3,4).
当y=﹣4时,x2﹣3x﹣8=0,解得x=,
∴N2(,﹣4),N3(,﹣4),
综上所述,满足条件的点N的坐标为(3,4)或(,﹣4)或(,﹣4).
同课章节目录
