3.5 第2课时 圆周角定理的推论2---同步课件 2021-2022学年浙教版数学九年级上册(15张)
文档属性
| 名称 | 3.5 第2课时 圆周角定理的推论2---同步课件 2021-2022学年浙教版数学九年级上册(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 741.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第3章圆的基本性质
3.5
第2课时
圆周角定理的推论2
2.圆周角的特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
1.
圆心角与所对的弧的关系
圆心角的度数等于所对弧的度数
知识回顾
3.圆周角定理
同一条弧所对的圆周角等于它所对的圆心角的一半.
4.圆周角定理的一个推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
学习目标
1.经历探索圆周角定理的另一个推论的过程.
2.掌握圆周角定理的推论“在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
3.会运用上述圆周角定理的推论解决简单几何问题.
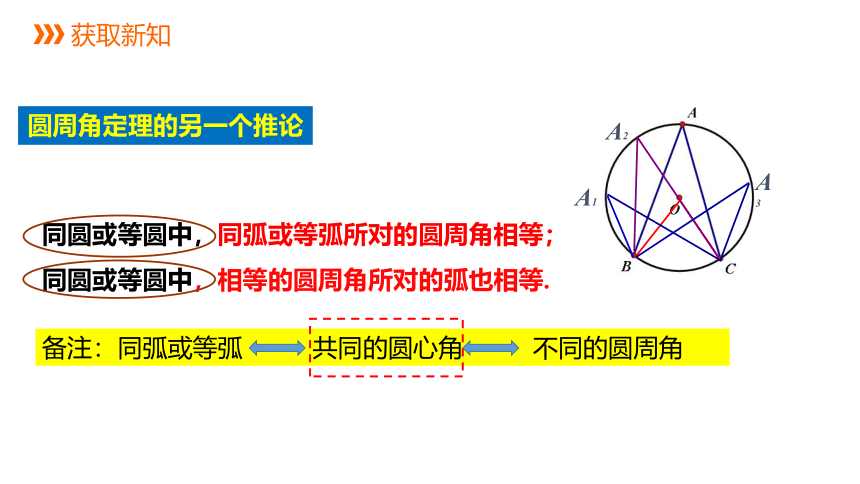
圆周角定理的另一个推论
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等.
A1
A2
A3
备注:同弧或等弧
共同的圆心角
不同的圆周角
获取新知
例1
已知:如图,△ABC内接于⊙O,∠ACB=2∠ABC,点D平分AB.求证:AC=BD.
例题讲解
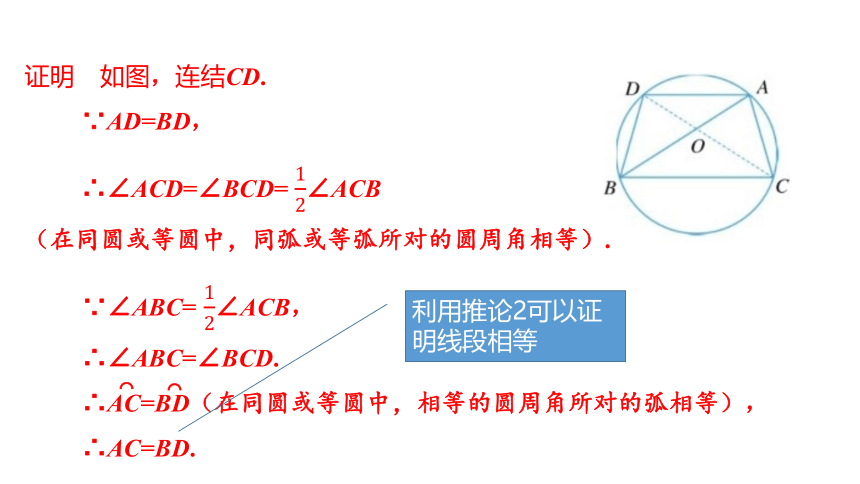
证明
如图,连结CD.
∵AD=BD,
∴∠ACD=∠BCD=
∠ACB
(在同圆或等圆中,同弧或等弧所对的圆周角相等).
∵∠ABC=
∠ACB,
∴∠ABC=∠BCD.
∴AC=BD(在同圆或等圆中,相等的圆周角所对的弧相等),
∴AC=BD.
⌒
⌒
利用推论2可以证明线段相等
例2
如图,有一个弓形的暗礁区,弓形所在圆的圆周角∠C=50°.问船在航行时怎样才能保证不进入暗礁区?
分析
由于暗礁区的圆心位置没有标明,怎样避开暗礁,可以从测量船到两个灯塔的张角(∠ASB)去考虑.船与暗礁区的相对位置可以通过∠ASB与∠ACB的大小关系来确定.请你自己写出求解过程.
1
如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15°
B.25°
C.30°
D.75°
2
如图,在⊙O中,AB=AC
,∠AOB=40°,则∠ADC
的度数是( )
A.40°
B.30°
C.20°
D.15°
⌒
⌒
C
C
随堂演练
∠DAB=∠DCB
利用推论2可以证明弧相等
思维拓展
利用推论2可以作记策
课堂小结
作业:
同步课时作业
第3章圆的基本性质
3.5
第2课时
圆周角定理的推论2
2.圆周角的特征:
①
角的顶点在圆上.
②
角的两边都与圆相交.
1.
圆心角与所对的弧的关系
圆心角的度数等于所对弧的度数
知识回顾
3.圆周角定理
同一条弧所对的圆周角等于它所对的圆心角的一半.
4.圆周角定理的一个推论:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
学习目标
1.经历探索圆周角定理的另一个推论的过程.
2.掌握圆周角定理的推论“在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
3.会运用上述圆周角定理的推论解决简单几何问题.
圆周角定理的另一个推论
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等.
A1
A2
A3
备注:同弧或等弧
共同的圆心角
不同的圆周角
获取新知
例1
已知:如图,△ABC内接于⊙O,∠ACB=2∠ABC,点D平分AB.求证:AC=BD.
例题讲解
证明
如图,连结CD.
∵AD=BD,
∴∠ACD=∠BCD=
∠ACB
(在同圆或等圆中,同弧或等弧所对的圆周角相等).
∵∠ABC=
∠ACB,
∴∠ABC=∠BCD.
∴AC=BD(在同圆或等圆中,相等的圆周角所对的弧相等),
∴AC=BD.
⌒
⌒
利用推论2可以证明线段相等
例2
如图,有一个弓形的暗礁区,弓形所在圆的圆周角∠C=50°.问船在航行时怎样才能保证不进入暗礁区?
分析
由于暗礁区的圆心位置没有标明,怎样避开暗礁,可以从测量船到两个灯塔的张角(∠ASB)去考虑.船与暗礁区的相对位置可以通过∠ASB与∠ACB的大小关系来确定.请你自己写出求解过程.
1
如图,在⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15°
B.25°
C.30°
D.75°
2
如图,在⊙O中,AB=AC
,∠AOB=40°,则∠ADC
的度数是( )
A.40°
B.30°
C.20°
D.15°
⌒
⌒
C
C
随堂演练
∠DAB=∠DCB
利用推论2可以证明弧相等
思维拓展
利用推论2可以作记策
课堂小结
作业:
同步课时作业
同课章节目录
