2.6探索勾股定理（1）

(共20张PPT)
直角三角形有哪些特殊性质？
A
B
C
∟
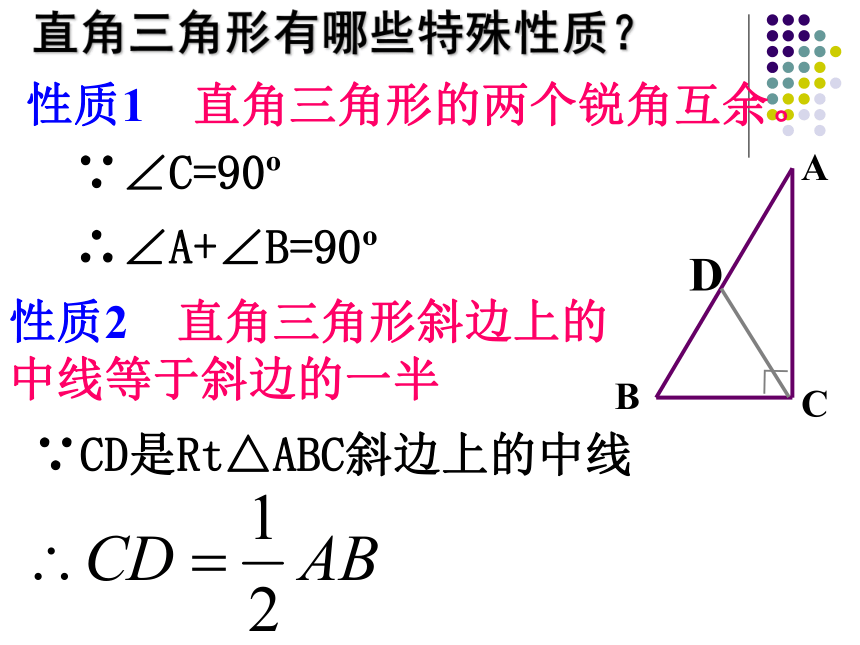
性质1 直角三角形的两个锐角互余。
性质2 直角三角形斜边上的中线等于斜边的一半
∵∠C=90
∴∠A+∠B=90
D
∵CD是Rt△ABC斜边上的中线
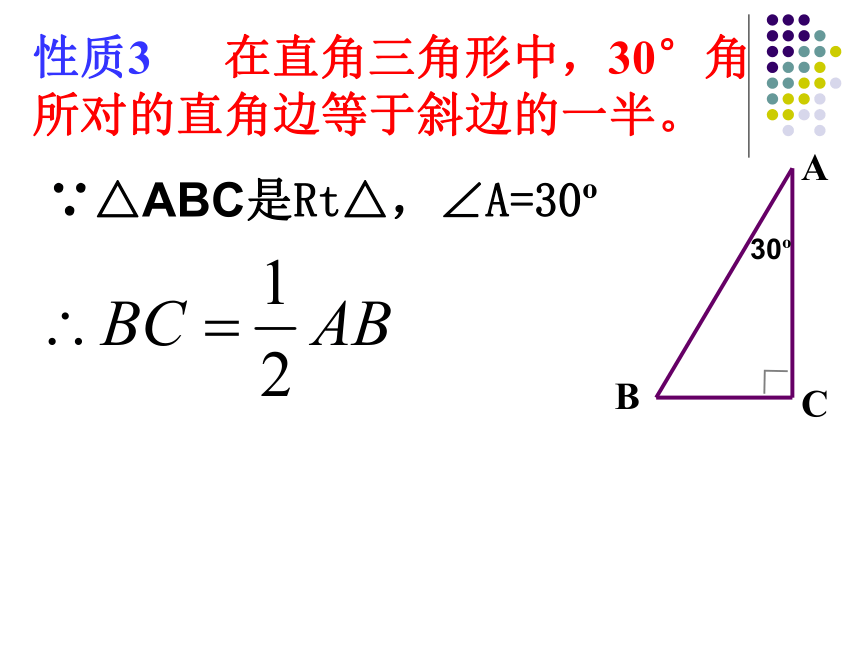
性质3 在直角三角形中，30°角所对的直角边等于斜边的一半。
A
B
C
∟
30
∵△ABC是Rt△，∠A=30
画一画
画Rt△ABC，使两直角边
1. AC=3cm，BC=4cm，
2.AC=５cm , BC=12cm ,
量一量斜边AB的长度
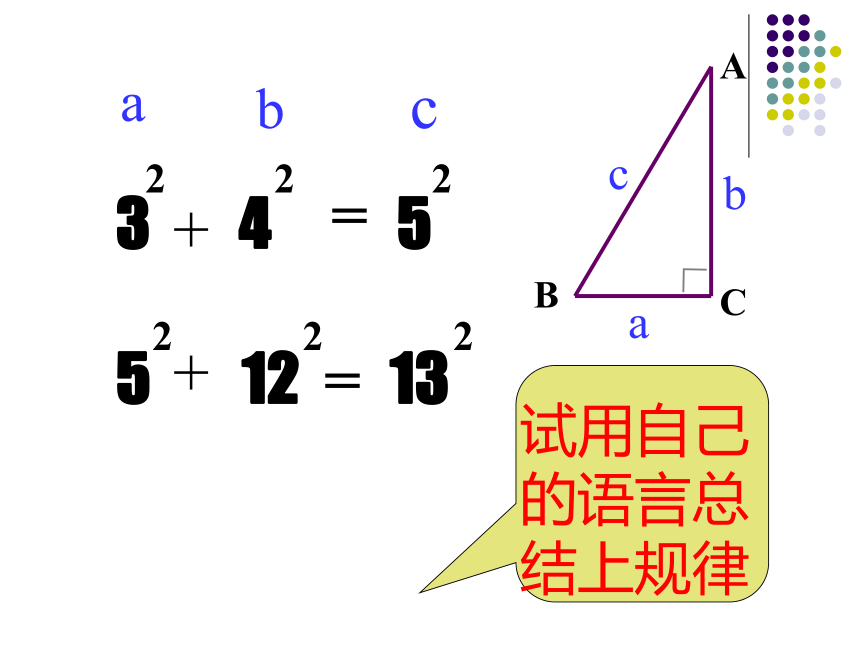
4 5
5 12 13
找找下列各边的关系:
2
2
2
2
2
2
+
+
=
=
试用自己
的语言总
结上规律
a
b
c
A
B
C
∟
a
b
c
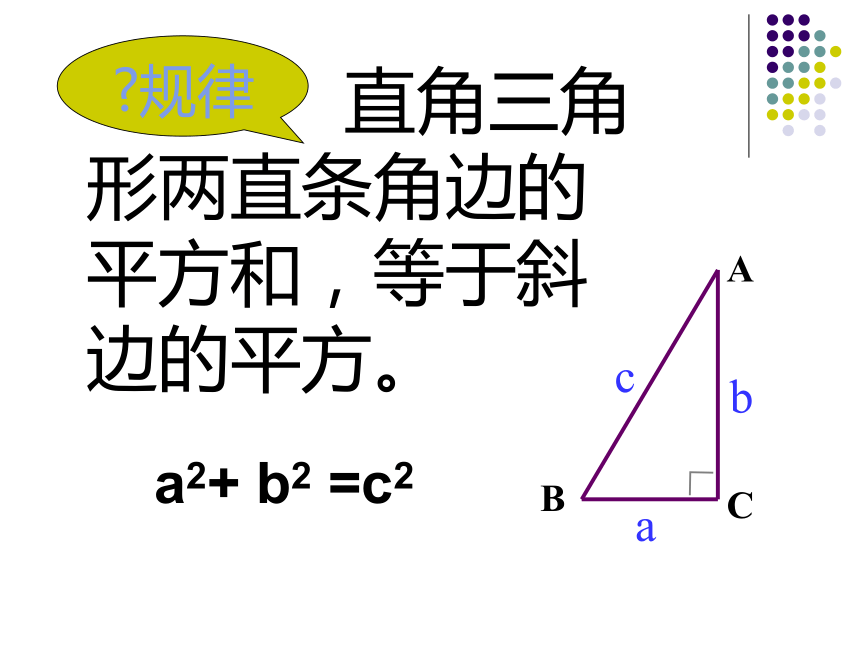
直角三角形两直条角边的平方和，等于斜边的平方。
规律
a2+ b2 =c2
A
B
C
∟
a
b
c
勾股定理：直角三角形两直角边的平方和 等于斜边的平方
（1）我国古代西周时期商高说法
C
A
B
a
b
c
股
勾
弦
3
4
5
　　 毕达哥拉斯定理
西方人认为最早发现直角三角形具有“勾2+股2=弦2”这一性质并
且最先给出严格证明的是古
希腊的数学家毕达哥拉斯（Pythagoras，约公元前
580－公元前500）．
我国至今可查的有关勾股定理的最早记载，是大约公
元前1世纪前后成书
的《周髀算经》比
毕达哥拉斯要早
发现500多年。
（1）赵爽的“弦图”
a
b
c
a2+ b2 =c2
赵爽的“弦图”的证法是世界上最简单的勾股定理的证法
曾被用为2002年国际数学家大会的会标
（2）毕达哥拉斯定理：
AC +BC = AB
Q
P
A
C
B
R
P+Q=R
（3）美国总统证法：
b
c
a
b
c
a
A
D
C
D
∴a +b =c
勾股定理
直角三角形两直角边
a,b的平方和，等于斜边c
的平方. 即 a2+ b2 =c2
c2 = a2 + b2
a2 = c2 - b2
b2 = c2 - a2
如图，在Rt△ABC中, ∠c = 90°
（1）若a=1，b=2，求c
A
C
B
a
c
b
解：根据勾股定理
c2 = a2+b2
∵C 0
=12+22=5
∟
∴
如图，在Rt△ABC中, ∠c = 90°
A
C
B
a
c
b
（2）若 AB=17，AC=15，求BC
∟
b
解：根据勾股定理
BC2 = AB2-AC2
∵BC 0
=172-152=64
∴ BC=8
已知在Rt△ABC中， ∠c = 90°，AB=c,BC=a,AC=b.
(1)如果， 求c
（2）如果c=34, a：b=8 ：15,
求a,b。
1.利用作直角三角形，在数轴上表示下列点
0
3
2
2.用刻度尺和圆规作一条线段，使它的长度为
能力
训练
1.已知 ,如图△ABC中， ∠ACB=90°,AC=12，BC=5，CD⊥AB，求CD的长度。
2.直角三角形有两边长为3和4，则第三边长为多少？
3.已知等边三角形的边长为2，则高线长为多少？