5.2平行四边形课件1

(共20张PPT)
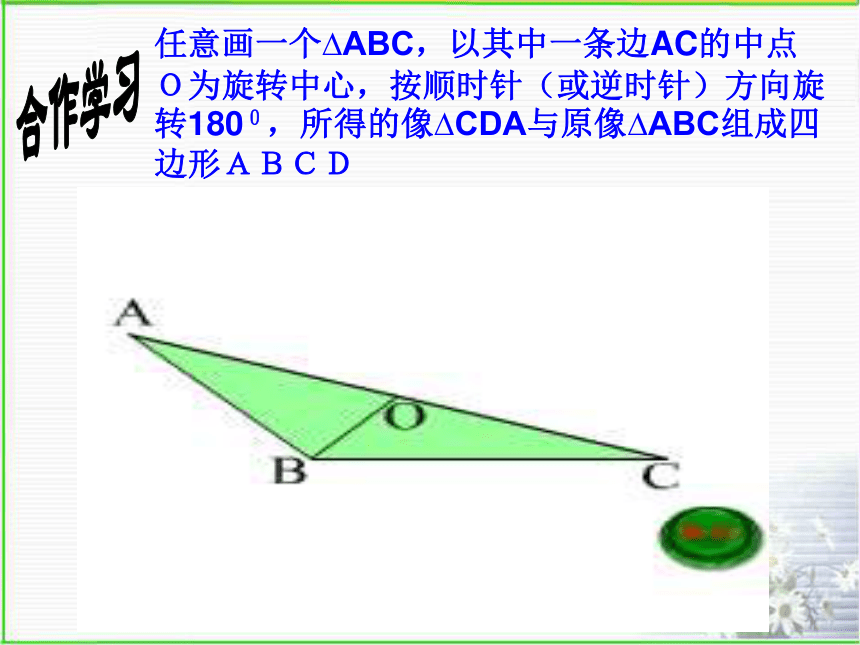
任意画一个 ABC，以其中一条边AC的中点Ｏ为旋转中心，按顺时针（或逆时针）方向旋转180０，所得的像 CDA与原像 ABC组成四边形ＡＢＣＤ
A
B
C
D
O
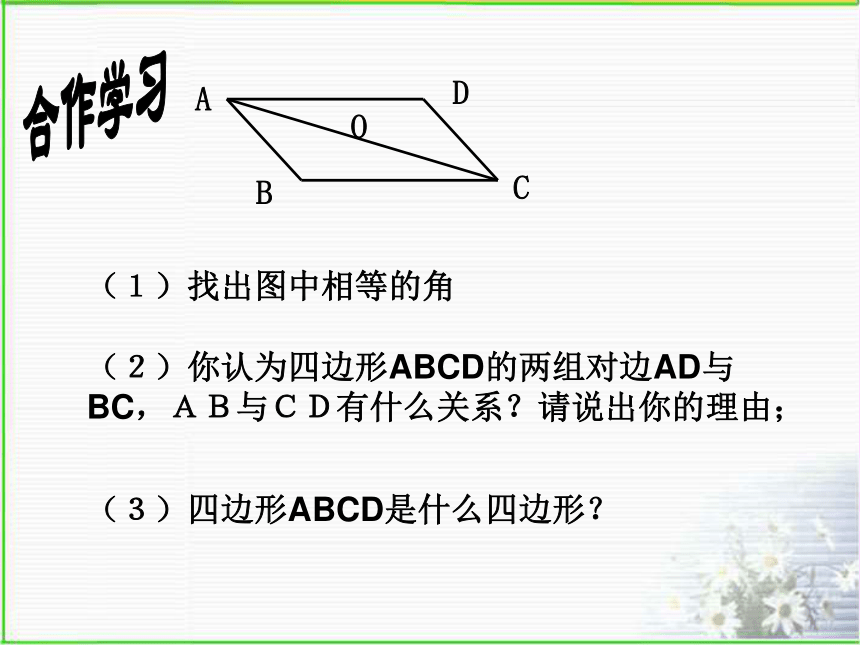
（１）找出图中相等的角
（２）你认为四边形ABCD的两组对边AD与BC，ＡＢ与ＣＤ有什么关系？请说出你的理由；
（３）四边形ABCD是什么四边形？
两组对边分别平行
四边形
平行四边形
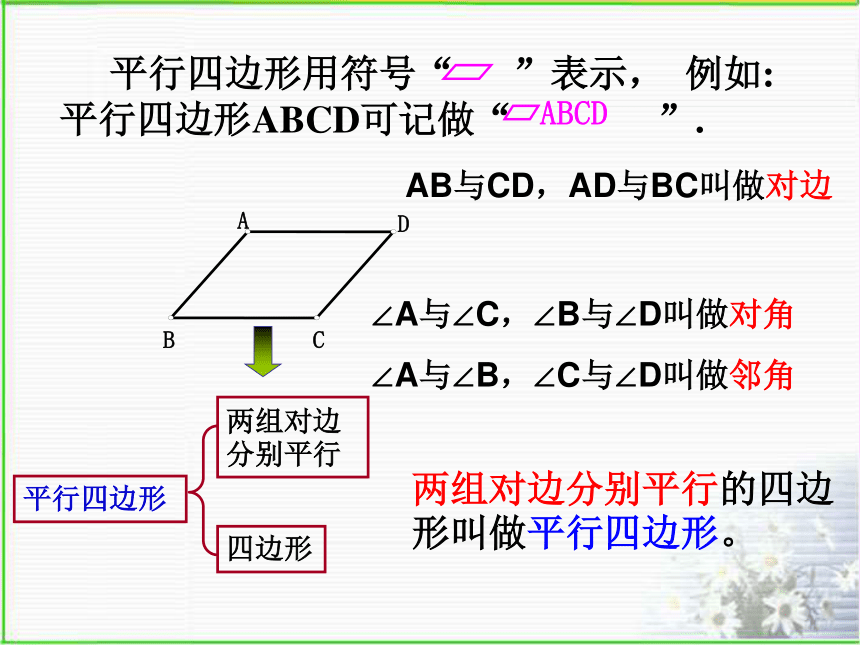
平行四边形用符号“ ”表示， 例如: 平行四边形ABCD可记做“ ”.
ABCD
∠A与∠C，∠B与∠D叫做对角
AB与CD，AD与BC叫做对边
∠A与∠B，∠C与∠D叫做邻角
两组对边分别平行的四边形叫做平行四边形。
A
D
C
B
∴四边形ABCD是平行四边形
∴ AB∥CD, BC∥AD
A
D
C
B
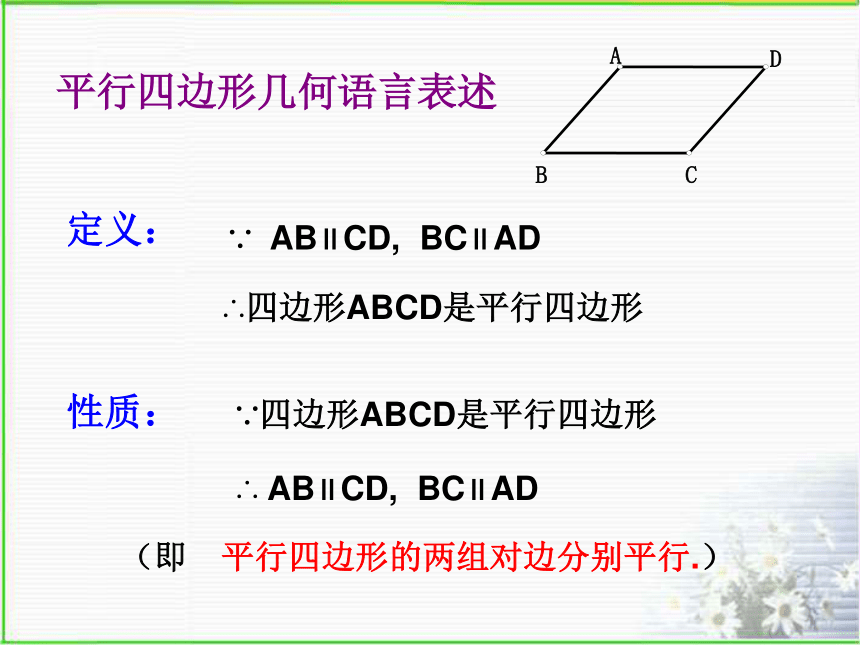
定义：
∵ AB∥CD, BC∥AD
性质：
∵四边形ABCD是平行四边形
（即　平行四边形的两组对边分别平行.）
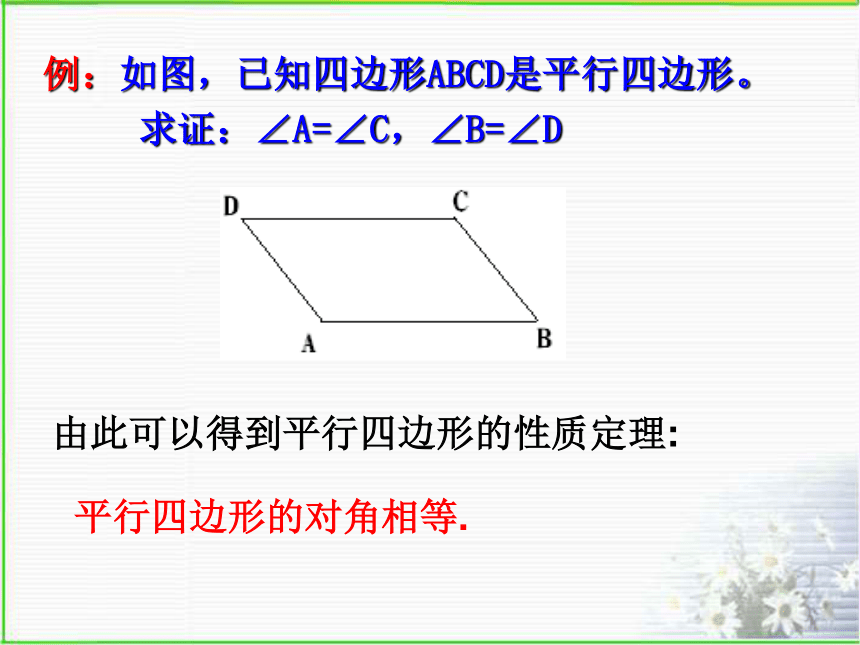
例：如图，已知四边形ABCD是平行四边形。
求证：∠A=∠C，∠B=∠D
由此可以得到平行四边形的性质定理:
平行四边形的对角相等.
1、在 ABCD中，已知∠B=55°，则∠A=______，∠C=_______，∠D=______ 。
2、已知平行四边形相邻两个角的度数之比为3:2,求平行四边形的各个内角的度数.
125o
55o
125o
108o、72o、108o、72o
3、已知平行四边形的最大角比最小角大100o ,求平行四边形的各个内角的度数.
40o、140o、40o、140o
练一练：
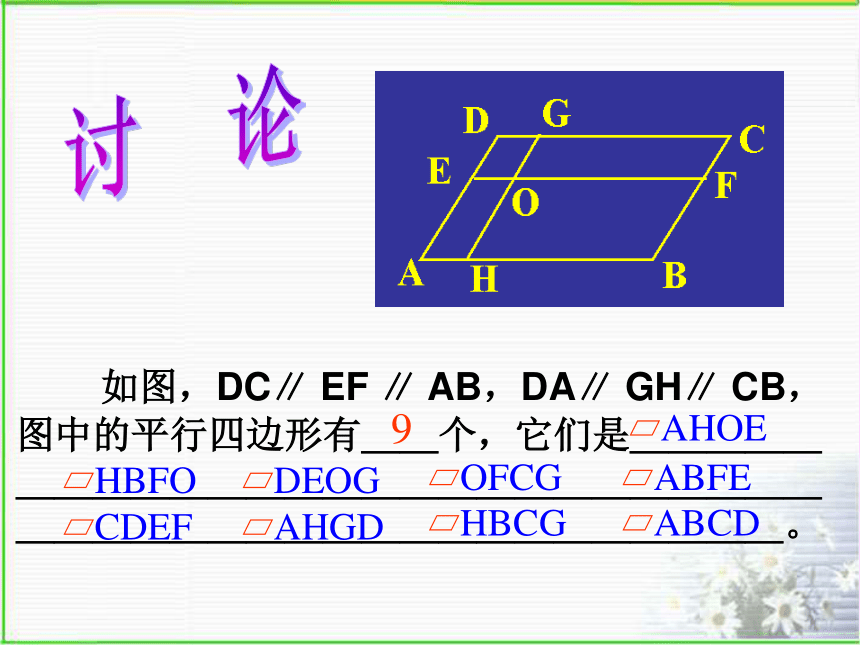
如图，DC∥ EF ∥ AB，DA∥ GH∥ CB，图中的平行四边形有＿＿个，它们是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
9
AHOE
ABCD
HBCG
AHGD
CDEF
ABFE
OFCG
DEOG
HBFO
平行四边形的不稳定性在生活中的应用
如图，四边形ABCD是平行四边形，则：
1）∠ADC= , ∠BCD= ；
2）边AB= ,BC = .
D
C
B
A
580
28
32
58°
28
32
122°
A
B
D
C
26°
47°
如图，四边形ABCD是平行四边形，
则： ∠BAC＝
107°
3cm
A
B
D
C
5cm
4cm
求　ABCD的面积
A
B
D
C
E
9cm
5cm
如图，四边形ABCD是平行四边形，若BE平分∠ABC，则ED＝
4cm
1
2
3
5cm
5cm
4cm
4、在 ABCD 中， ∠ADC=125°， ∠CAD=21°，求∠ABC， ∠CAB的度数.
课堂小结
1、平行四边形的定义：两组对边分别平行的四边形。
2、平行四边形的对角相等。
3、平行四边形的不稳定性在实际生活中的应用。