5.2平行四边形课件2

(共16张PPT)
平行四边形小结与复习
一、四边形知识结构图
二、典型例题讲解
三、课堂巩固练习
四、小结与课外作业
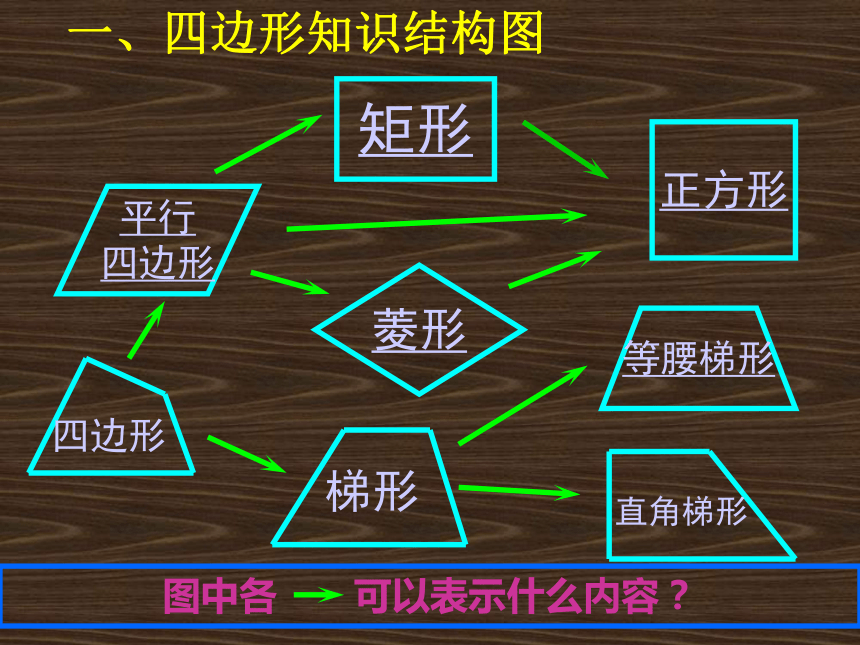
一、四边形知识结构图
四边形
平行
四边形
矩形
菱形
正方形
梯形
等腰梯形
直角梯形
图中各 可以表示什么内容？
四边形
平行四边形
矩 形
菱 形
正方形
梯 形
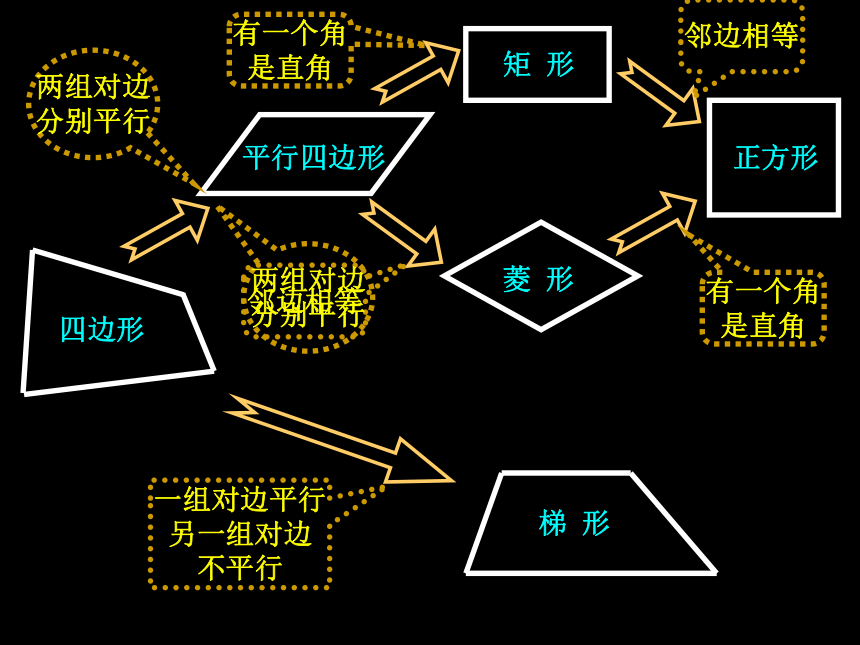
两组对边
分别平行
有一个角
是直角
邻边相等
邻边相等
有一个角
是直角
一组对边平行
另一组对边
不平行
两组对边
分别平行
A
B
C
D
O
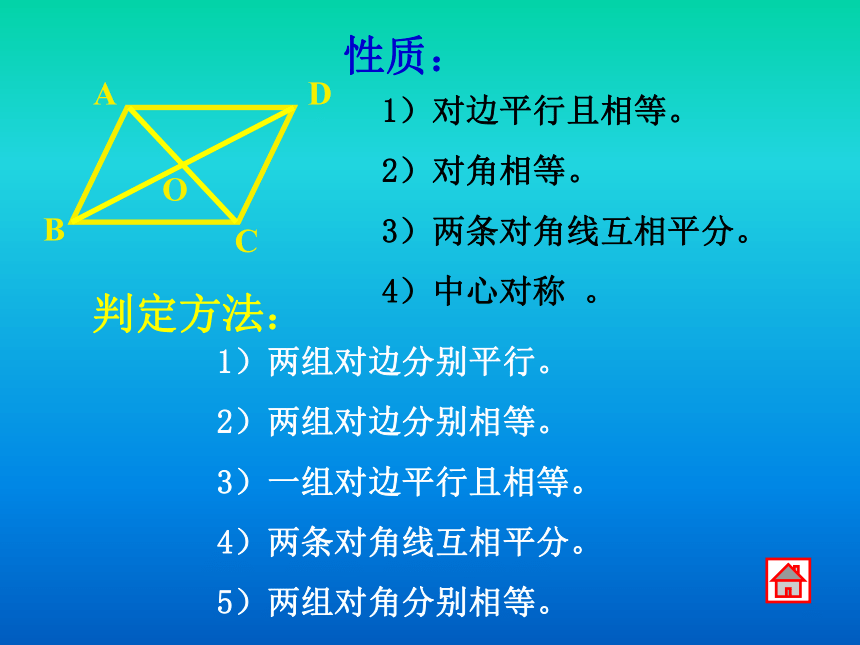
性质：
1）对边平行且相等。
2）对角相等。
3）两条对角线互相平分。
4）中心对称 。
判定方法：
1）两组对边分别平行。
2）两组对边分别相等。
3）一组对边平行且相等。
4）两条对角线互相平分。
5）两组对角分别相等。
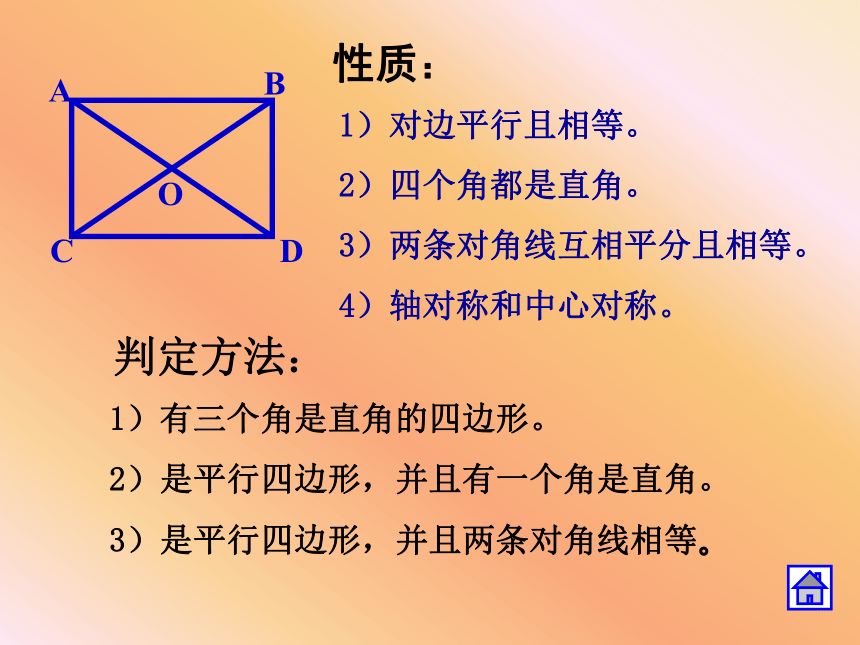
A
B
C
D
O
性质：
1）对边平行且相等。
2）四个角都是直角。
3）两条对角线互相平分且相等。
4）轴对称和中心对称。
判定方法：
1）有三个角是直角的四边形。
2）是平行四边形，并且有一个角是直角。
3）是平行四边形，并且两条对角线相等。
C
A
B
D
O
性质：
1）对边平行，四条边都相等 。
2）对角相等。
3）两条对角线互相垂直平分 ，
每条对角线平分一组对角。
4）轴对称和中心对称。
判定方法：
1）四条边都相等的四边形。
2）是平行四边形，并且有一组邻边相等。
3）是平行四边形，并且两条对角线互相垂直。
A
B
C
D
O
性质：
1）对边平行，四条边都相等 。
2）四个角都是直角。
3）两条对角线互相垂直平分且相等，
每条对角线平分一组对角。
4）轴对称和中心对称。
判定方法：
1）是矩形，并且有一组邻边相等。
2）是菱形，并且有一个角是直角。
3）是平行四边形，并且有一组邻边相等
和有一个角是直角。
A
B
C
D
性质：
1）两底并行，两腰相等。
2）同一底上的两个角相等。
3）两条对角线相等。
4）轴对称。
判定方法：
1）是梯形，并且同一底上的两个角相等。
2）是梯形，并且两条对角线相等。
O
几种平行四边形的性质及比较
元素
图形
边
角
对角线
对边相等，对边平行
对边相等，对边平行
对边相等，对边平行
四条边都相等
对边相等，对边平行
四条边都相等
对角相等，邻角互补
对角相等，邻角互补
对角相等，邻角互补
四个角都是直角
对角相等，邻角互补
四个角都是直角
对角线互相平分
对角线互相平分
对角线相等
对角线互相平分
对角线互相垂直，且每条对角线平分一组对角
对角线互相平分
对角线互相垂直、相等，且每条对角线平分一组对角
几种平行四边形的判定及比较
边
角
对角线
两组对过分别平行的四边形；
有一个角是直角的平行四边形；
有一组邻边相等的平行四边形；
两组对角分别相等的四边形
三个角是直角的四边形
对角线互相平分的四边形
对角线相等的平行四边形
四条边都相等的四边形
一级对边平行且相等的四边形；
两组对边分别相等的四边形
对角线互相垂直的平行四边形
有一组邻边相等且有一个角是直角的平行四边形
（既是矩形又是菱形）
元素
图形
无
无
一、判断题：
1）两条对角线相等且互相垂直的四边形是矩形. ( )
2）两条对角线互相垂直平分的四边形是菱形. ( )
3）两条对角线互相垂直的矩形是正方形. ( )
4）两条对角线相等的菱形是正方形. ( )
5）两条对角线垂直且相等的平行四边形是正方形.( )
6）两条对角线垂直且相等的四边形是正方形. ( )
课堂练习
二、填空题：
(1) 已知平行四边形ABCD中，∠A∶∠B＝1∶2，
则∠C＝ °，∠D＝ °。
(2)顺次连结菱形四边中点所得的四边形是 。
(3)梯形的高为6,面积为42,则梯形的中位线的长是 。
(4)梯形的上底长为6cm,中位线长为8cm,则下底长为 。
√
√
╳
╳
√
√
60
120
矩形
7
10cm
三、选择题：
(1)菱形ABCD的周长为20cm，∠ABC＝120°,
则对角线BD等于（ ）
（A）4cm（B）6cm（C）5cm（D）10cm
(2)下列图形既是轴对称图形又是中心对称图形的是( )
(A)等腰三角形 (B)矩形 (C)平行四边形 (D)等腰梯形
(3)矩形、菱形、正方形都具有的性质是（ ）
（A）对角线相等 （B）对角线互相平分
（C）对角线平分一组对角 （D）对角线互相垂直
C
B
B
A
B
D
C
二、课外作业：
一、小结：
1) 要求掌握各种特殊四边形的概念、性质和判定定理，
知道这些图形之间的联系与区别，并能运用有关知
识进行证明和计算。
2）做题时，常常需要添加辅助线，灵活地添加辅助线
可以把问题简化，应注意在这方面进行积累。
3）随着知识的丰富，解决问题的方法增多了，当遇到
一个问题有多种解法时，要注意选取简单的解法。
三角形中位线定理 三角形的中位线平行于第三边，
并且等于第三边的一半。
A
B
C
D
E
DE∥BC，DE＝1/2 BC
A
D
B
C
E
F
梯形中位线定理 梯形的中位线定理平行于两底，
并且等于两底和的一半。
EF∥AD∥BC，
EF＝1/2 (AD+BC)
例２ 已知：AD是△ABC的中线，E是AD的中点，F是BE的延长线与AC的交点。求证：AF＝1/2 FC。
A
B
C
D
E
F
G
证明:过点D作DG∥AC交BF于点G。∴∠GDE＝∠FAE 。
∵E是AD的中点。
∴DE＝AE。又∵∠GED＝∠FEA。
∴△DEG≌△AEF
∴DG＝AF。
∵DG∥AC，BD＝DC。
∴BG＝GF。
∴DG是△BCF的中线。
∴DG＝1/2 FC。
∴AF＝1/2 FC。
H
证明：过点D作DH∥BF
交AC于点H。
∵AD是△ABC的中线。
∴D是BC的中点。
∴CH＝HF＝1/2 CF。
∵E是AD的中点，EF∥DH。
∴AF＝FH。
∴AF＝1/2 FC。
方法1
方法2
例１ 已知: 如图，矩形ABCD中，E是BC上一点，DF AE于F，若AE＝BC，求证: CE＝FE.
Ａ
Ｂ
Ｃ
Ｄ
Ｅ
Ｆ
分析：从求证入手，要证CE＝FE，由已知AE＝BC可知，只要证AF＝BE即可，而AF、BE分别在△AFD、△EBA中，即要证明△AFD≌△EBA .
证明：∵四边形ABCD是矩形，
∴ AD＝BC＝AE， B＝90 ， AD∥BC 。 ∴ DAE＝ AEB。
又∵ DF AE于F， ∴ AFD＝ 90 ＝ B 。∴ △AFD≌△EBA . ∴ AF＝BE ,
∵ AE＝BC ∴ AE－AF＝BC－BE 即 CE＝FE