7.4分式方程1

(共15张PPT)
7.4 分式方程（一）
观察下列方程：
分式方程：方程中只含有分式，或分式和整式，且分母中含有未知数的方程.
下列方程中，哪些是分式方程？哪些是整式方程？
回顾与思考
整式方程
分式方程
整式方程
分式方程
根式方程
分式方程
分式方程
例题欣赏
例1、
解：7(x+3)=2(2x-3)
7x+21=4x-6
7x-4x= -6-21
3x= -27
x= -9
经检验：x= -9是原方程的根
∴原方程的根是x= -9
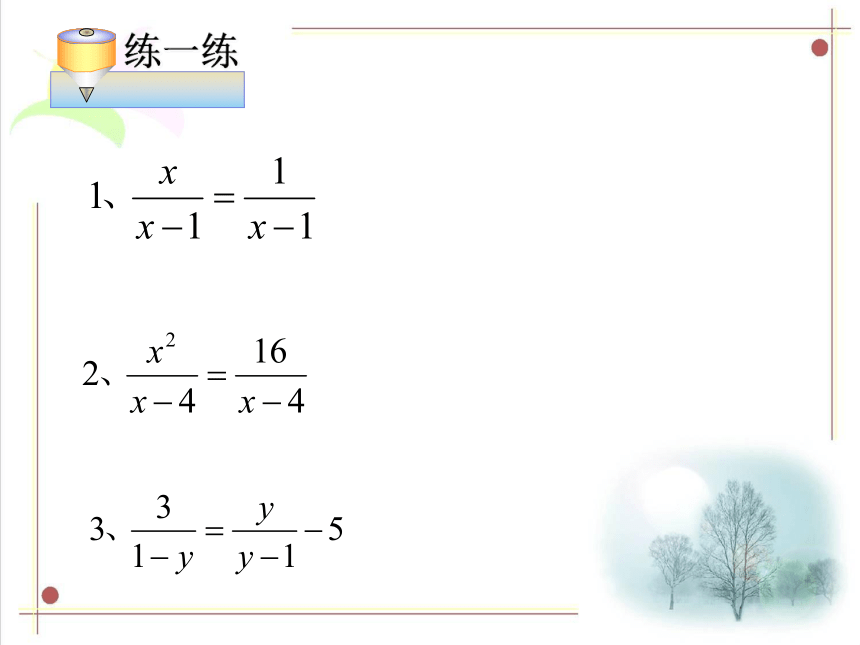
练一练
例题欣赏
例2、
使分母为零的根叫增根
验根的方法：将方程的解代入最简公分母，使分母为零的根叫增根。
没有分母的项不要漏乘
解：2-x= -1-2(x-3)
∴x=3
经检验：x=3是增根
∴原方程无解
练一练
解分式方程的一般步骤：
（1）在方程的两边都乘以最简公分母，约去分母化成整式方程
（2）解这个整式方程
（3）把方程的根代入最简公分母，检验是否等于零；把方程的根代入原方程，检验左右两边是否相等
（4）结论
你能否从中总结出分式方程 的解法呢？
例题欣赏
例3、
练一练
例题欣赏
例4、
练一练
2、若分式方程 有增根x=2，则 a= 。
x=2
1、如果　 有增根，那么增根为 。
-1
解分式方程一般步骤：
去分母，化为整式方程；
(1)把各分母分解因式;
(2)找出各分母的最简公分母;
(3)方程两边每一项乘以最简公分母;
解整式方程；
检验；
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
结论 ：确定分式方程的解.
这里的检验要以计算正确为前提
温馨提示
(1)去分母时，原方程整式部分不要漏乘即每一项都需乘以最简公分母。
(2)约去分母后，分子是多项式时，要注意添括号．
(3)增根要舍掉.
(4)不要忘了结论.
小结
在解分式方程中你有何收获与体会.
一化二解三检验
现在你还有什么疑惑吗？