三角形单元复习与巩固

三角形单元复习与巩固
类型一：数学思想方法的应用
1．分类思想
　　1．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为( )．
　　A．60°　　　 B．120°　　　 C．60°或150°　　　 D．60°或120°
　　思路点拨：锐角三角形的高都在三角形的内部，钝角三角形的高有两条在三角形的外部，应进行分类讨论．
　　答案：D.
　　总结升华：三角形的高与三角形的形状有关，应进行分类讨论.
　　举一反三：
　　【变式1】已知BD、CE是△ABC的高，直线BD、CE相交所成的角中有一个角为50°，则∠BAC的度数为__.
　　【答案】50°或130°
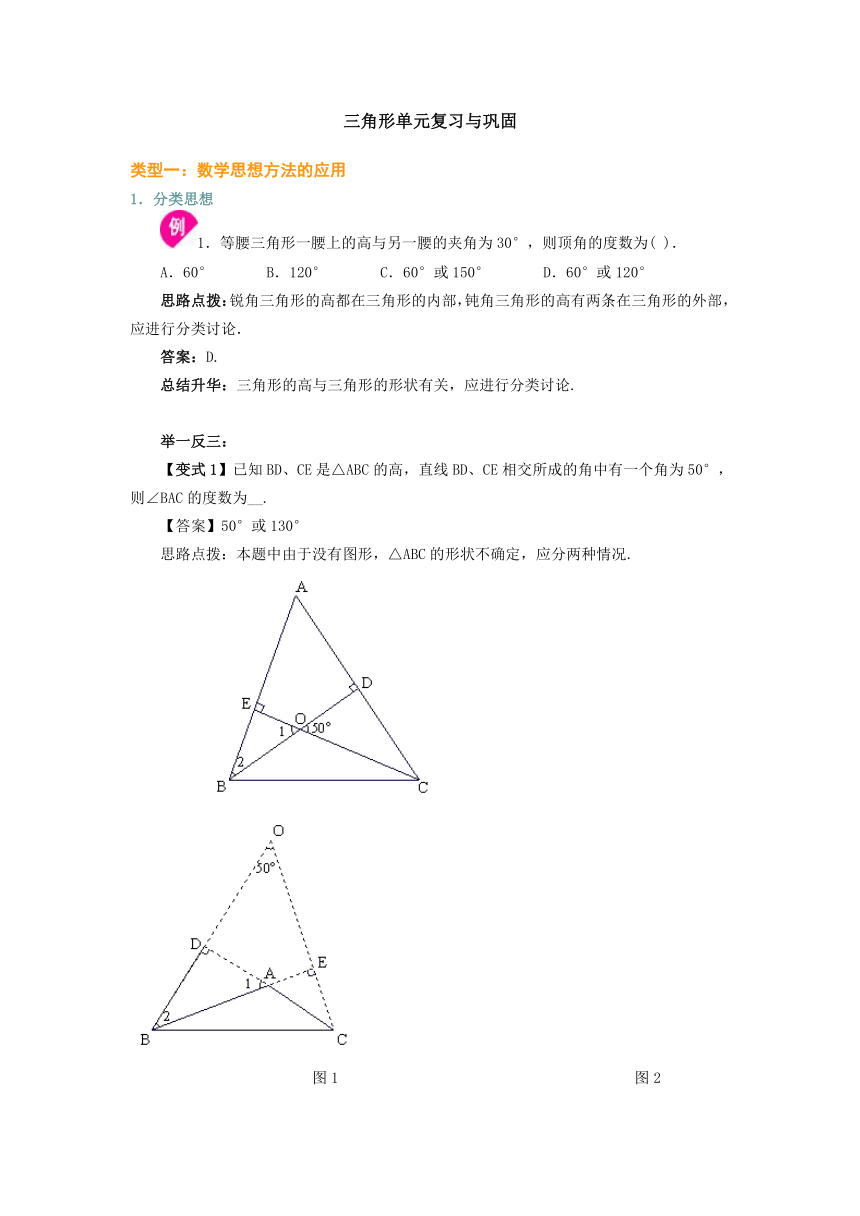
　　思路点拨：本题中由于没有图形，△ABC的形状不确定，应分两种情况.
　　　　　　　　　
　　　　　　　　　　　　图1　　　　　　　　　　　　　　　　　　　 图2
　　如图1所示，△ABC是锐角三角形，因为BD、CE是△ABC的高，所以△BOE、△BAD都是直角三角形，则　　∠A+∠2＝90°，∠1+∠2＝90°，所以∠A＝∠1＝50°，即∠BAC＝50°.
　　如图2所示，△ABC是钝角三角形，因为BD、CE是△ABC的高，所以△ABD、△OBE都是直角三角形，则　　∠1+∠2＝90°，∠O+∠2＝90°，所以∠1＝∠O＝50°，所以∠BAC＝180°－∠1＝180°－50°＝130°.
　　【变式2】有四条线段，它们的长分别为1cm，2cm，3cm，4cm，从中选出三条组成三角形，正确的选法有(　　)
　　A、1种　　　　B、2种　　　C、3种　　　　D、4种
　　解析：从四条线段中任选三条，共有4种选法：①1cm，2cm，3cm；②1cm，2cm，4cm；③1cm，3cm，4cm；④2cm，3cm，4cm，其中能构成三角形的选法只有④2cm，3cm，4cm，故选A。
　　答案：A
　　总结升华：判断三条线段能否构成三角形，只要检验两条较短(小)线段之和能否大于第三条线段即可。若大于，则能构成三角形；否则，不能。
2．转化思想
　　2．(1)如图1是一个五角星ABCDE，请算出∠A+∠B+∠C+∠D+∠E的大小.
　　　　　　(2)如图2，3，4，5的变式图形中，上面的结论成立吗？为什么
　　思路点拨：本题是一题多变题，先求出图1中各角之和，其他图形是否有相同的结论同理可证.
　　　　　　　
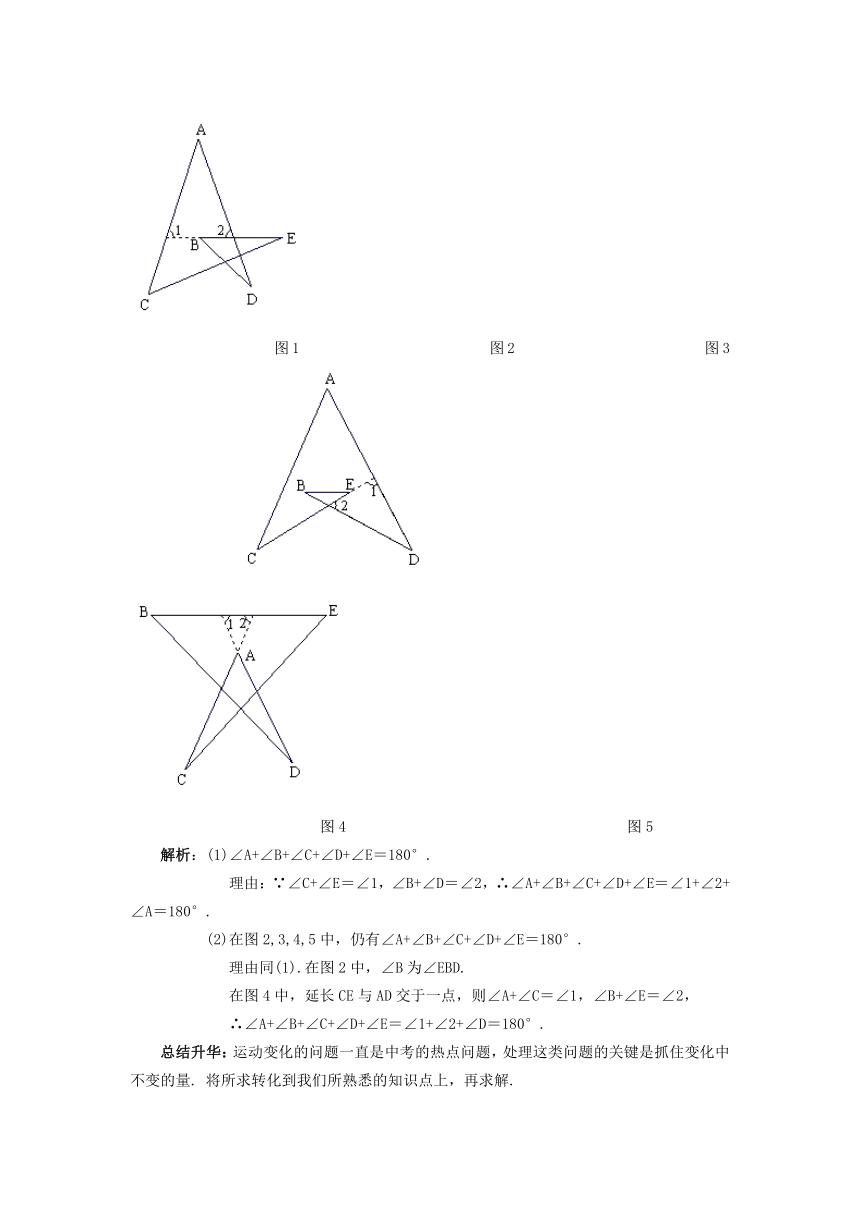
　　　　　　　　　 图1 　　　　　　　　　　　　图2 　　　　　　　　　　　　图3
　　　　　　　　　　　　
　　　　　　　　　　　　 图4 　　　　　　　　　　　　　　　　　　图5
　　解析：(1)∠A+∠B+∠C+∠D+∠E＝180°.
　　　　　　 理由：∵∠C+∠E＝∠1，∠B+∠D＝∠2，∴∠A+∠B+∠C+∠D+∠E＝∠1+∠2+∠A＝180°.
　　　　　(2)在图2,3,4,5中，仍有∠A+∠B+∠C+∠D+∠E＝180°.
　　　　　　 理由同(1).在图2中，∠B为∠EBD.
　　　　　　 在图4中，延长CE与AD交于一点，则∠A+∠C＝∠1，∠B+∠E＝∠2，
　　　　　　 ∴∠A+∠B+∠C+∠D+∠E＝∠1+∠2+∠D＝180°.
　　总结升华：运动变化的问题一直是中考的热点问题，处理这类问题的关键是抓住变化中不变的量. 将所求转化到我们所熟悉的知识点上，再求解.
　　举一反三：
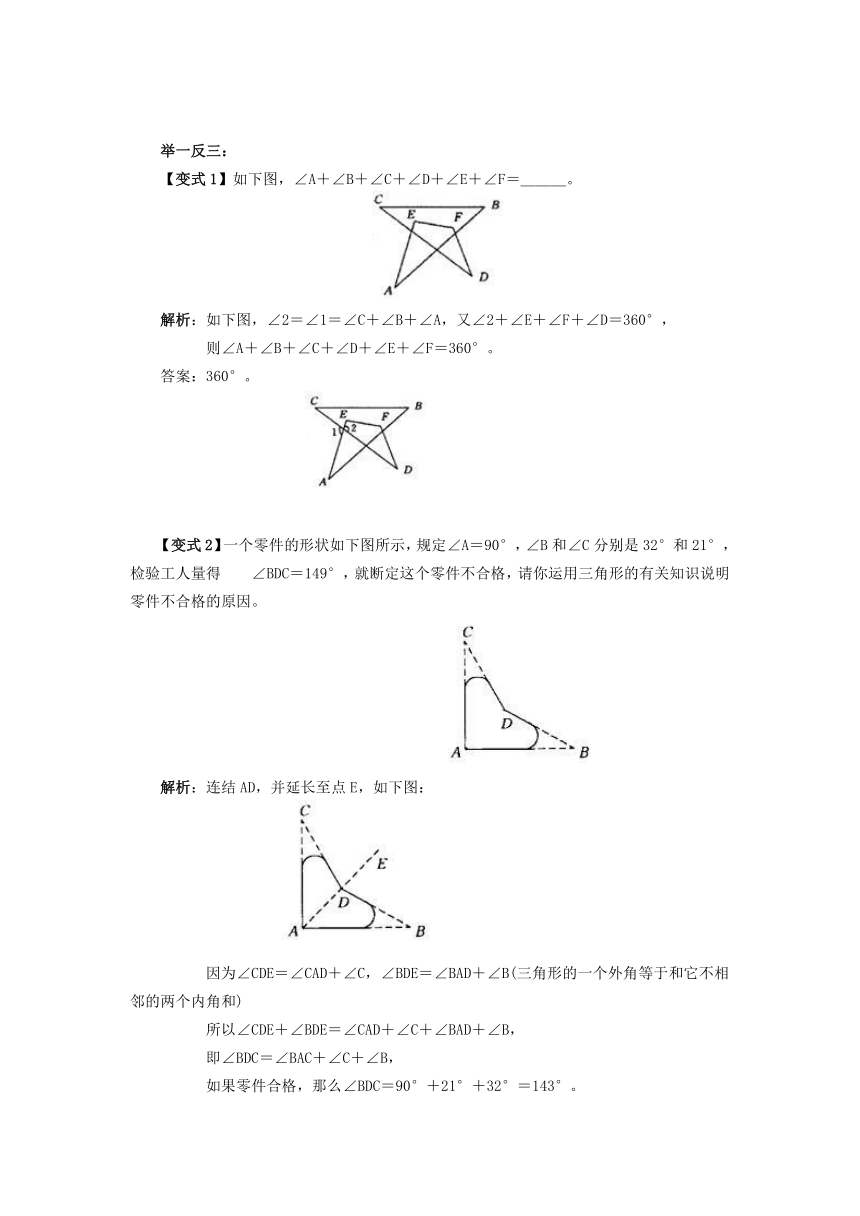
　　【变式1】如下图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝＿＿＿。
　　　　　　　　　　　　　　　　
　　解析：如下图，∠2＝∠1＝∠C＋∠B＋∠A，又∠2＋∠E＋∠F＋∠D＝360°，
　　　　　则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝360°。
　　答案：360°。
　　　　　　　　　　　
　　【变式2】一个零件的形状如下图所示，规定∠A＝90°，∠B和∠C分别是32°和21°，检验工人量得　　∠BDC＝149°，就断定这个零件不合格，请你运用三角形的有关知识说明零件不合格的原因。
　　　　　　　　　　　　　　　　　　　　　
　　解析：连结AD，并延长至点E，如下图：
　　　　　　　　　　
　　　　　因为∠CDE＝∠CAD＋∠C，∠BDE＝∠BAD＋∠B(三角形的一个外角等于和它不相邻的两个内角和)
　　　　　所以∠CDE＋∠BDE＝∠CAD＋∠C＋∠BAD＋∠B，
　　　　　即∠BDC＝∠BAC＋∠C＋∠B，
　　　　　如果零件合格，那么∠BDC＝90°＋21°＋32°＝143°。
　　　　　而现量得∠BDC＝149°，所以零件不合格。
3．方程思想
　　3．在△ABC中，∠B＝20°+∠A，∠C＝∠B－10°，求∠A的度数.
　　思路点拨：由三角形的内角和，建立方程解决.
　　解析：∵∠C＝∠B－10°＝∠A+10°，由三角形的内角和定理，
　　　　　得∠A+∠B+∠C＝∠A+∠A+20°+∠A+10°＝180°，∴∠A＝50°.
　　总结升华：本题根据三角形的内角和定理列出以∠A为未知数的方程，解方程即可求得∠A.建立方程求解，是本章求解角度数的常用方法.
　　举一反三：
　　【变式1】如下图，若等腰三角形中，一腰上的中线把它的周长分为15cm和6cm的两部分，求该三角形各边的长。
　　　　　　　　　　　　　　　　　　　
　　解：设腰长为xcm，底边长为ycm，分两种情况
　　　　(1)　　∴
　　　　(2) 　∴
　　　　∵4＋4＜13，不能形成三角形，应舍去。
　　　　∴等腰三角形三边长分别为10cm，10cm，1cm。
　　【变式2】已知从多边形一个顶点出发的所有对角线，将多边形分成三角形的个数恰好等于该多边形所有对角线条数，求多边形内角和。
　　思路点拨：根据从n边形一个顶点引出的对角线，把多边形分成(n－2)个三角形，共有条对角线，列出方程，先求出多边形的边数n，再进一步求内角和。
　　解析：设该多边形为n边形，则从一个顶点引出的对角线，把多边形分成(n－2)个三角形，
　　　　　共有条对角线。
　　　　　根据题意得n－2＝。解之，得n＝4或n＝1(舍去)
　　　　　∴该多边形的内角和为(4－2)·180°＝360°。
类型二：三角形内角和定理
　　4. 如图所示，已知D是AB上一点，E是AC上的一点，BE、CD相交于点F，∠A＝62°，∠ACD＝15°，∠ABE＝20°.
　　(1)求∠BDC的度数；
　　(2)求∠BFD的度数；
　　(3)试说明∠BFC＞∠A.
　　　　　　　　　　　　　　　　　　
　　思路点拨：∠BDC是△ADC的一个外角，由三角形的外角性质：三角形的一个外角等于与它不相邻的两个内角的和；三角形的一个外角大于与它不相邻的任何一个内角. 可以求出∠BDC和∠BFC均大于∠A。然后根据三角形内角和定理，求出∠BFD。
　　解析：(1)∵∠BDC＝∠A+∠ACD，∴∠BDC＝62°+15°＝77°；
　　　　　(2)∵∠ABE+∠BDC+∠BFD＝180°，∴∠BFD＝180°－20°－77°＝83°；
　　　　　(3)∵∠BFC是△DBF的一个外角，∴∠BFC＞∠BDC. ∵∠BDC是△ADC的一个外角，
　 　　　　　∴∠BDC＞∠A. ∴∠BFC＞∠A.
　　总结升华：求一个角的度数，我们应该首先弄清这个角在哪个三角形中，是外角还是内角，跟已知的角有什么联系。
　　举一反三：
　　【变式1】已知：如图，在ΔABC中，∠A∶∠B∶∠C＝3∶4∶5，BD、CE分别是边AC、AB上的高，BD、CE相交于H，求∠BHC的度数。
　　　　　　　　　　　　　　　　　　
　　思路点拨：由已知可求出∠A、∠B、∠C，在RtΔABD中，∠1＝90°－∠A，在RtΔBEH中，∠2＝90°－∠1，而∠2是∠BHC的邻补角，∴∠BHC＝180°－∠2即可求出。
　　解析：设∠A＝3x，则∠B＝4x，∠C＝5x
　　　　　∴3x＋4x＋5x＝180°(三角形内角和定理)
　　　　　∴x＝15°
　　　　　∴∠A＝45°，∴∠1＝90°-45°＝45°，∠2＝90°－∠1=45°
　　　　　∴∠BHC＝135°
　　【变式2】如图，已知D为ΔABC内任一点，求证：∠BDC＞∠ABD。
　　　　　　　　　　　　　　
　　思路点拨：要证∠BDC＞∠ABD，这两个角度没有直接关系，如连结AD并延长，则在ΔABD中有∠1＞∠ABD，而∠BDC＞∠1，所以∠BDC＞∠ABD。
　　证明：过D作射线AE
　　　　　在ΔABD中有∠1＞∠ABD(三角形的一个外角大于和它不相邻的任何一个内角)
　　　　　∵∠BDC＞∠1(如图)
　　　　　∴∠BDC＞∠ABD(不等式性)
　　【变式3】（2010辽宁锦州）如图所示，∠BDC=98°，∠C=38°，∠B=23°，∠A的度数是（ ）
　　　　　　　　　　　　　　　　　　　　　　
　　A．61° 　　B．60° 　　C．37° 　　D．39°
　　【答案】C
　　解析：连接BC，则∠CBD+∠BCD=180°-∠BDC=180°-98°=82°．
　　　　　在△ABC中，有∠C=38°，∠B=23°，
　　　　　则∠A=180°-∠ACD-∠ABD-(∠CBD+∠BCD)=180°-38°-23°-82°=37°．
类型三：三角形三边性质
　　5．如图，点P是△ABC内一点，比较BP+CP与AB+AC的大小.
　　　　　　　　　　　　　　
　　思路点拨：三边关系是说明不等式问题的首选方法，寻找或构造一个新的三角形，使它与已知的两个三角形联系起来.
　　解析：延长BP交AC于点Ｄ，则AB+AD＞BD，
　　　　　即AB+AD＞BP+PD. ①
　　　　　而PD+DC＞CP. ②
　　　　　①+②得AB+AD+PD+DC＞BP+PD+CP，
　　　　　∴AB+AC＞BP+CP.
　　总结升华：通过作辅助线，构造三角形，利用三角形的两边之和大于第三边. 在这两个不等式中，PD起了桥梁的作用.
　　举一反三：
　　【变式1】不等边三角形的边长都是整数，且周长是12，这样的三角形共有＿＿个。
　　解析：设三角形的三边为a，b，c，且a＜b＜c。
　　　　　根据三角形三边关系，得a＋b＞c。所以a＋b＋c＞2c。
　　　　　由题意，得a＋b＋c＝12。所以2c＜12，即c＜6。
　　　　　因为a，b，c都是整数，所以c＝3或4或5。
　　　　　当c＝3时，由于c是最长边，不满足周长为12，舍去；
　　　　　当c＝4时，由于c是最长边，不满足周长为12，舍去；
　　　　　当c＝5时，则a＝3，b＝4，满足周长为12，符合题意。
　　　　　所以符合题意的三角形共有1个。
　　答案：1
　　【变式2】已知：如图，P为ΔABC内任一点。求证：PA＋PB＋PC＞(AB＋BC＋AC)
　　　　　　　　　　　　　　　　　　
　　思路点拨：一般证明结论有分数系数时，常把它化成整系数证明，故结论变为：2(PA＋PB＋PC)＞AB＋BC＋AC
　　而由PA、PB、PC、AB、BC、AC组成三个小三角形，即ΔABP、ΔBCP、ΔACP。
　　根据三角形三边关系定理有
　　AP＋BP＞AB　①
　　BP＋CP＞BC　②
　　AP＋CP＞AC　③
　　由①＋②＋③得结论。
　　证明：在ΔABP、ΔPBC、ΔAPC中有
　　　　　AP＋BP＞AB　①
　　　　　BP＋CP＞BC　②
　　　　　AP＋CP＞AC　③
　　　　　(三角形两边之和大于第三边)
　　　　　∴①＋②＋③得，2(AP＋BP＋CP)＞AB＋BC＋AC
　　　　　∴AP＋BP＋CP＞(AB＋BC＋AC)
类型四：实践应用
　　6．某公园便道用三种不同的正多边形地砖铺设，其中已选好了用正十二边形和正方形两种，还需要选用__________，使这三种组合在一起把便道铺满.
　　思路点拨：当围绕一点拼在一起的几个多边形的内角和加在一起恰好组成一个周角时，就能拼成一个平面图形.
　　解析：分别计算正十二边形与正方形每个内角的度数，它们分别为150°和90°，
　　　　　再用360°－150°－90°＝120°，每个内角为120°的正多边形为正六边形.
　　　　　另外正三角形的两个内角和也为120°，所以正三角形也可以.
　　　　　所以还需选用正六边形或正三角形.
　　总结升华：用两种以上边长相等的正多边形组合成平面图形，实质上是相关正多边形“交接处各角之和能否拼成一个周角”的问题。
　　举一反三：
　　【变式】(烟台市中考题)现有四种地面砖，它们的形状分别是：正三角形.正方形.正六边形.正八边形，且它们的边长都相等．同时选择其中两种地面砖密铺地面，选择的方式有( )
　　A．2种　　　 B．3种　　　 C．4种 　　　D．5种
　　解析：几个多边形围绕一点拼在一起时，当内角加在一起恰好组成一个周角时就能铺地面。易知正三角形的每个内角为60度，正方形的每个内角为90度，正六边形的每个内角为120度，正八边形的每个内角为135度，那么正三角形与正方形、正三角形与正六边形、正方形与正八边形都可分别密铺地面，所以有3种选择的方式。
　　答案：B
　　7．餐馆的厨房有一块90cm长，54cm宽的长方形墙面准备贴上瓷砖，现在已经买了18cm×12cm的瓷砖24块，6cm×6cm的瓷砖三块，请你帮忙设计一种铺设方案，并说明设计意图.
　　思路点拨：此类问题应先进行有关的运算，再寻找合理的设计方案．
　　解析：18cm×12cm的瓷砖长宽相差6cm，按图1所示那样拼，中间会出现一个边长为6cm的小正方形，正好放下一块6cm×6cm的瓷砖，即每块6cm×6cm的瓷砖周围需要18cm×12cm的瓷砖4块，所以3块6cm×6cm的瓷砖按图2所示的方法连续平铺，然后在大长方形的上、下各平铺5块18cm×12cm的瓷砖，则形成了一个90cm×54cm的大长方形，即把长为90cm，宽54cm的长方形墙面贴满瓷砖.
　　　　　 　　　　　　　　　　　　　
　 　　　　　　　　　　图1　　　　　　　　　　　　　　　　图2
　　总结升华：对于寻找合理的设计方案，首先要进行有关的运算，然后分情况进行分析及论证，选择最佳方案。
　　举一反三：
　　【变式】如图，某部队在灯塔A周围进行爆破作业，A的周围3千米内的区域为危险区域，有一渔船误入离A为2千米的B处，为了尽快驶离危险区域，该船应沿哪条射线方向航行？
　　(要求给予证明)
　　　　　　　　　　　　　　　　　　　　　
　　解析：该船应沿射线AB方向驶离危险区域。
　　证明如下：如图，设射线AB交⊙A于点C，再在⊙A上任取一点D(不在直线AB上，且不与点C重合)。
　　　　　　　连结AD、BD，进而在ΔABD中有AB＋BD＞AD(三边关系定理)
　　　　　　　但半径AD＝AC＝AB＋BC，∴AB＋BD＞AB＋BC，∴BD＞BC。