二元一次方程组的应用

(共20张PPT)
应用二元一次方程组解决实际问题的基本步骤:
理解问题 (审题,搞清已知和未知,分析数量关系)
制订计划(考虑如何根据等量关系设元,列出方程组)。
执行计划（列出方程组并求解，得到答案）。
回顾(检查和反思解题过程,检验答案的正确性以及是否符合题意).
例 1、 已知一个两位数，十位数字比个位数字大3 ，将十位数字与个位数字对调所得的新数比原数小27，求这个两位数。
十位 个位 三位数的代数式
原数
新数
若设十位数字为x，个位数字为y，则
x
y
10x+y
y
x
10y+x
X=y+3
10y+x+27=10x+y
例2、小强和小明非常喜欢遥控汽车，放学后,去邮局邮购遥控汽车,邮局里,小强和小明商量如何购买,最后决定在A、B、C三款中做选择,其中A款每个48元;　B款每个78元;　C款每个98元.
选择A和B,选择A和C,选择B和C.
问题一:若选择其中两款有几种选择方法
问题二:若选择其中两款共5个,用了340元(邮费除外),你知道他们是如何选择的吗
(1)选择A和B
设购买A款汽车x个,则
购买B款汽车(5-x)个,故
(2)选择A和C
78x+48(5-x)=340
解得: x=
故不符合题意!
设购买A款汽车x个,则
购买C款汽车(5-x)个,故
48x+98(5-x)=340
解得: x=3
解:
A款:3个,C款:5－３=2个
(3)选择B和C
设购买B款汽车x个,则
购买C款汽车(5-x)个,故
78x+98(5-x)=340
解得: x=
故不符合题意!
答:小强家购买A款纪念品3个,C款纪念品2个.
题后反思：
1.分类讨论思想.
2.实际问题必须要检验.
例3、某车间有28名工人,每人每天平均能生产螺栓10个或螺帽15个.
问题一:应分配多少人生产螺栓,多少人生产螺
帽,才能使当天生产的螺栓和螺帽刚好配套
x
28-x
10x
15(28-x)
解：
设制作螺栓的有x人,则
制作螺帽的有(28-x)人.
由题意可得:
解得:x＝12(人)
答:制作头饰的有16人,制作娃娃的有12人.
28-12=16(人)
2×10x=15(28-x)
螺栓
螺帽
总个数
人数
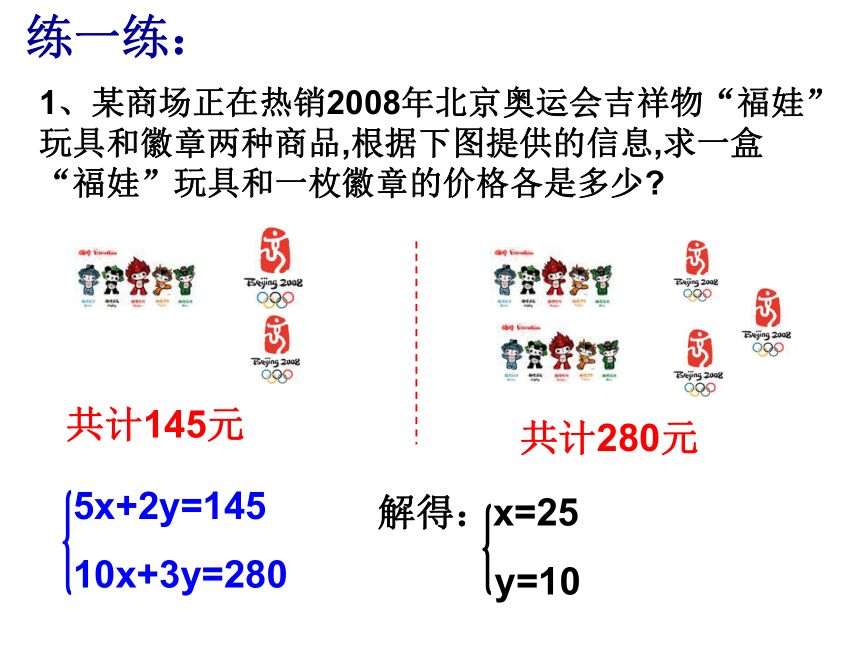
1、某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种商品,根据下图提供的信息,求一盒“福娃”玩具和一枚徽章的价格各是多少
共计145元
共计280元
练一练：
5x+2y=145
10x+3y=280
解得：x=25
y=10
2、八年级3班在召开期末总结表彰会前,班主任安排班长李小波去商店购买奖品,下面是李小波与售货员的对话:
李小波:阿姨,您好！
售货员:同学,你好,想买点什么
李小波:我只有100元,请帮我安排买10 支钢笔和15本 笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗
3、今年五月27日,印尼中爪哇省发生强烈地震,给当地人民造成巨大损失.某校积极组织捐款支援灾区,初三(1)班55名共捐款500元,捐款情况如下表:
捐款(元)
人数
5
8
10
12
6
7
表中捐款8元和10元的人数不小心被墨水污染已看不清楚,请你帮助确定表中数据,并说明理由.
4、某酒店客房部有三人间,双人间客房,收费数据如下表:
三人间
双人间
普通(元/间/天)
豪华(元/间/天)
150
140
300
400
为吸引游客,实行团体入住五折优惠措施,一个50人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房.若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人普通间和双人普通间客房各多少间
5、某工厂第一季度生产甲,乙两种机器共480台,改进生产技术后,计划第二季度这两种机器共554台,其中甲种机器产量比第一季度增产10﹪,乙种机器产量比第一季度增产20﹪,该厂第一季度生产甲,乙两种机器各多少台
联想集团有A型、B型、C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元，我市某中学计划将100500元钱全部用于购进其中两种不同型号的电脑共36台，请你设计出几种不同的购买方案，并说明理由。
反思：未知数不只两个，为了解决问题方便，所以设三个未知数以帮助解决问题，把问题割裂开来看，仍属于二元一次方程组，在一个问题里面设三个未知数，这本身就是一种创造性思维。
开放性问题
1、我区某学校原计划向内蒙察右后旗地区的学生捐赠3500册图书,实际共捐赠4125册,其中初中学生捐赠了原计划的120﹪,高中学生捐赠了原计划的115﹪.问初中学生和高中学生各比原计划多捐赠了图书多少册
解:设原计划初中学生捐赠x册,高中学生捐赠y册,
根据题意,得 x+y=3500
120﹪x+115﹪y=4125
解得 x=2000
y=1500
∴ (120﹪-1)x=400 (115﹪-1)y=225.
2、王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44000元,其中种茄子每亩用了1700元,获纯利2400元;种西红柿每亩用了1800元,获纯利2600元.问王大伯一共获纯利多少元
解:设王大伯种了x亩茄子,y亩西红柿
根据题意,得 x+y=25
1700x+1800y=44000
解得, x=10
y=15
共获利:2400×10+2600×15=63000
3、初一(2)班的一个综合实践活动小组去A、B两个超市调查去年和今年“五一节”期间的销售情况,下面是调查后小敏与甲,乙两同学进行交流的情景.根据他们的对话,请你分别求出A、B两个超市今年“五一节”期间的销售额.
小敏:两超市销售额去年共为150万元,今年共为170万元.
甲:A超市销售额今年比去年增加15﹪;
乙:B超市销售额今年比去年增加10﹪.
4、近几年我省高速公路建设有了较大的发展，有力地促进我省的经济建设。正在修建中的某段高速公路要招标，现有甲，乙两个工程队。若甲，乙两个队合做，24天完成，需费用120万元；若甲单独做20天后，剩下的工程由乙做，还需40天才能完成，这样需费用110万元。问：
（1）甲，乙两队单独完成此项工程，各需多少天？
（2）甲，乙两队单独完成此项工程，各需多少万元？
（1）30天，120天。
（2）135万元，60万元。
5、某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1000张,已知体彩中心有A,B,C三种不同价格的彩票,进价分别是A彩票每张1.5元,B彩票每张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,用去45000元,请你设计进票方案;
设购进A彩票x张,B彩票y张,C彩票z张.
(1)只够进A种彩和B种彩票,依题意可列方程组
x+y=1000×20
1.5x+2y=45000 解得x＜0,所以无解.
只够进A种彩和C种彩票,依题意可列方程组
x+z=1000×20 x=5000
1.5x+2.5z=45000 ∴ z=15000
只购进B种彩票和C种彩票,依题意可列方程组
y+z=1000×20 y=1000
2y+2.5z=45000 ∴ z=10000
综上所述,若经销商同时购进不同型号的彩票,共有两种方案可行.即A彩票5扎,C彩票15扎或 B彩票10扎,C彩票10扎.
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元, C型彩票一张获手续费0.5元.在购进两种彩票的方案中,为使销售完时获得手续费最多,你选择哪种进票方案
若购进种A彩票5扎，C种彩票15扎，
销售完后获手续费为０.２×５０００+０.５×１５０００
＝８５００（元）
若购进种Ｂ彩票１０扎，C种彩票1０扎，
销售完后获手续费为０.３×１００００+０.５×１００００
＝８０００（元）