暑期特训：图形与变换（1）

暑期特训：图形与变换（一）
重点、难点：
重点：通过学习轴对称、平移、旋转的学习应用于实际；
难点：轴对称、平移、旋转中的基本性质，并运用基本性质解决几何问题。
知识要点：
（1）图形的轴对称
　　①通过具体实例认识轴对称，探索它的基本性质，理解对应点所连的线段被对称轴垂直平分的性质。
　　②能够按要求作出简单平面图形经过一次或两次轴对称后的图形；探索简单图形之间的轴对称关系，并能指出对称轴。
　　③欣赏现实生活中的轴对称图形，结合现实生活中典型实例了解并欣赏物体的镜面对称，能利用轴对称进行图案设计。
（2）图形的平移
　　①通过具体实例认识平移，探索它的基本性质，理解对应点连线平行且相等的性质。
　　②能按要求作出简单平面图形平移后的图形。
　　③利用平移进行图案设计，认识和欣赏平移在现实生活中的应用。
（3）图形的旋转
　　①通过具体实例认识旋转，探索它的基本性质，理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质。
　　②能够按要求作出简单平面图形旋转后的图形。
　　③欣赏旋转在现实生活中的应用。
　　④探索图形之间的变换关系（轴对称、平移、旋转及其组合）。
　　⑤灵活运用轴对称、平移和旋转的组合进行图案设计。
【典型例题】
一、轴对称：
（一）基本性质：对应点所连的线段被对称轴垂直平分的性质。
例1. 如图，在内，点分别是点关于、的对称点，若的周长为15，求的长。
解：∵在内,点分别是点关于、的对称点，分别在直线上
∴与关于直线成轴对称，与关于直线成轴对称，
∴
又∵，的周长为15
∴
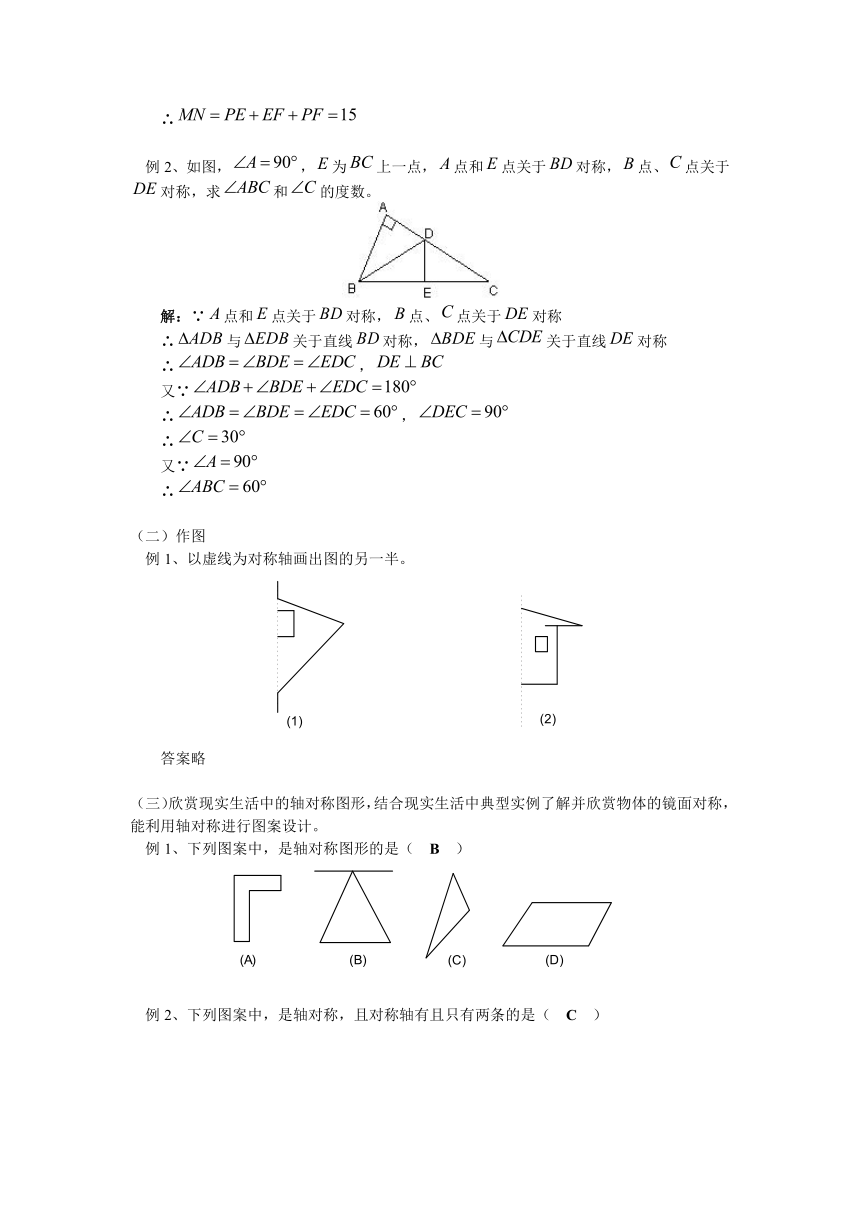
例2、如图，，为上一点，点和点关于对称，点、点关于对称，求和的度数。
解：∵点和点关于对称，点、点关于对称
∴与关于直线对称，与关于直线对称
∴，
又∵
∴，
∴
又∵
∴
（二）作图
例1、以虚线为对称轴画出图的另一半。
答案略
（三）欣赏现实生活中的轴对称图形，结合现实生活中典型实例了解并欣赏物体的镜面对称，能利用轴对称进行图案设计。
例1、下列图案中，是轴对称图形的是（ B ）
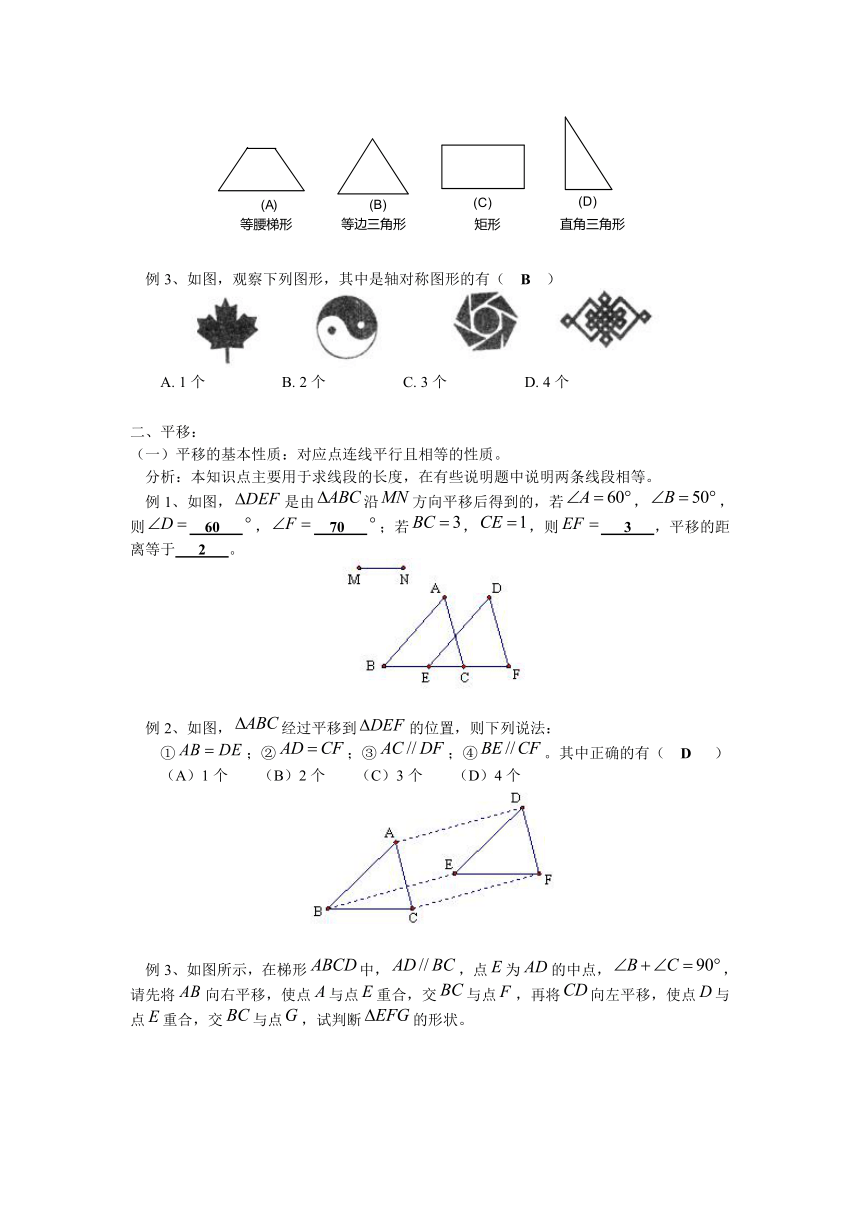
例2、下列图案中，是轴对称，且对称轴有且只有两条的是（ C ）
例3、如图，观察下列图形，其中是轴对称图形的有（ B ）
A. 1个 B. 2个 C. 3个 D. 4个
二、平移：
（一）平移的基本性质：对应点连线平行且相等的性质。
分析：本知识点主要用于求线段的长度，在有些说明题中说明两条线段相等。
例1、如图，是由沿方向平移后得到的，若，，则 60 ， 70 ；若，，则 3 ，平移的距离等于 2 。
例2、如图，经过平移到的位置，则下列说法：
①；②；③；④。其中正确的有（ D ）
（A）1个 （B）2个 （C）3个 （D）4个
例3、如图所示，在梯形中，，点为的中点，，请先将向右平移，使点与点重合，交与点，再将向左平移，使点与点重合，交与点，试判断的形状。
解：∵向右平移，使点与点重合，交与点；向左平移，使点与点重合，交与点
∴，
∴,
又∵
∴
∴
∴是直角三角形
例4、如图，原来是重叠的两个直角三角形，将其中一个三角形沿着BC方向平移BE的距离，就得到此图形，求阴影部分面积（单位：厘米）。
解：由题意可知：
∴
∴
（二）能按要求作出简单平面图形平移后的图形。
例1、按下列要求画出正确图形：
已知和线段，画出沿线段的方向平移3后的图形；
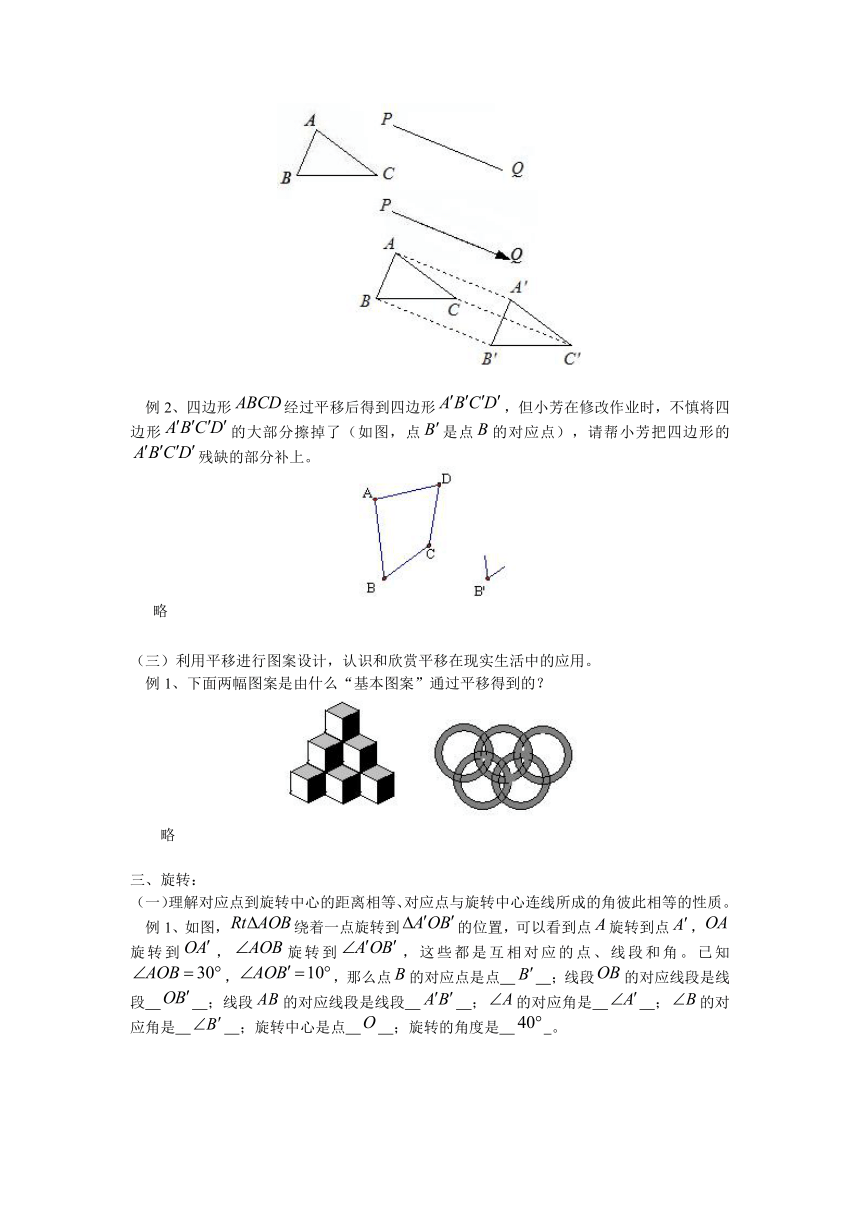
例2、四边形经过平移后得到四边形，但小芳在修改作业时，不慎将四边形的大部分擦掉了（如图，点是点的对应点），请帮小芳把四边形的残缺的部分补上。
略
（三）利用平移进行图案设计，认识和欣赏平移在现实生活中的应用。
例1、下面两幅图案是由什么“基本图案”通过平移得到的？
略
三、旋转：
（一）理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质。
例1、如图，绕着一点旋转到的位置，可以看到点旋转到点，旋转到，旋转到，这些都是互相对应的点、线段和角。已知，，那么点的对应点是点 ；线段的对应线段是线段 ；线段的对应线段是线段 ；的对应角是 ；的对应角是 ；旋转中心是点 ；旋转的角度是 。
例2、如图，正方形，是上一点，经过旋转后到达的位置。
①旋转中心是哪一点？A点
②旋转角度是多少度？
③旋转后的线段与原线段的位置有何关系？垂直
④如果是的中点，那么经过上述旋转后，点转到了什么位置？ AF中点
（二）能够按要求作出简单平面图形旋转后的图形。
例1、已知和点，画出绕点旋转的。
略
（三）欣赏旋转在现实生活中的应用。
例1、下图中，是旋转对称图形的有（ D ）
A. 8个 B. 9个 C. 10个 D. 11个
例2、下列各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是（ B ）
A. B. C. D.
（四）图形之间的变换关系（轴对称、平移、旋转及其组合），灵活运用轴对称、平移和旋转的组合进行图案设计。
例1、如图，在纸上画和两条直线。分三种情况分别画出关于直线对称的，再画出关于直线对称的。并观察和，你能发现这两个三角形有什么关系吗？
情况（1）：直线互相平行；
情况（2）：直线互相垂直；
情况（3）：直线相交但不垂直。
解：情况（1）如图所示，和是平移的关系，平移的方向就是点到点的方向，平移的距离是线段的长度。
情况（2）如图所示，和成中心对称的关系，对称中心是直线的交点。
情况（3）如图所示，和成旋转对称的关系，旋转中心是直线的交点，旋转角度是的度数。
【模拟试题】（答题时间：45分钟）
一、选择题
1. 如图所示，下列各项的两个图形，由左边的图形变换到右边的图形， 需要轴对称变换的是（ ）
2. 图中是万花筒的一个图案。图中所有的小三角形都是等边三角形，其中的菱形AEFG可以看作是把菱形ABCD以A为中心怎样得到的（ ）
A. 顺时针旋转60°
B. 逆时针旋转60°
C. 逆时针旋转120°
D. 顺时针旋转120°
3. 如图所示，正方形ABCD通过旋转得到正方形AB′C′D′，则旋转的角度为（ ）
A. 30° B. 45° C. 60° D. 90°
4. 图中可以看作是一个菱形通过几次旋转得到的，每次可能旋转（ ）
A. 3次，150° B. 5次，60° C. 3次，90° D. 6次，30°
5. 如图所示，△ABC平移之后得△DCE，下列说法正确的是（ ）
A. 点B的对应点是E B. 点C的对应点是C
C. 点C对应点是E D. 点C位置没变
二、填空题
1. 如图所示，△ACE，△ABF均为等腰直角三角形，∠BAF=∠EAC=90°， 那么△AFC以点A为旋转中心逆时针旋转90°之后与________重合，其中点F与点____对应， 点C与点_____对应.
2. 如图所示，△ABC为等边三角形，D是BC边上一点，△ABD经旋转后与△ACE重合，则旋转的中心是点_____，旋转的角度是______，点M对应点的位置在线段____上。
3. 在线段、角、等边三角形、正方形和圆中，是中心对称图形的有_______，是轴对称图形的有__________。
三、如图所示，下列图形都是旋转对称图形，它们分别最少要旋转多少度才能与原图形重合
四、学科内综合题
如图所示，在正方形的网格中有三个形状、大小完全一样的三角形，请说明如何运用轴对称、平移、旋转这三种运动，将它们都重合在一个图形上
五、创新题
用9根火柴杆搭成如图所示的图案，移动2根火柴杆，使这9 根火柴杆搭成一个中心对称图形，并画出此图形。
六、中考题
1. （2003，长沙）如下图所示，请根据小文在镜中的像写出他的运动衣上的实际号码__________。
2.（2003，江苏）有两个正方形花坛，准备把每个花坛都分成形状相同的四块，种不同的花草，图上边的两个图案是设计示例，请你在下边的两个正方形中再设计两个不同的图案。
3. （2003，福州）用若干根火柴杆可以摆出一些优美的图案，图中是用火柴杆摆出的一个图案，此图案表示的含义可以是天平（或公正）。请你用5根或5根以上的火柴杆摆成一个轴对称图案，并说明你画的图案的含义。
【试题答案】
一、1. C 2. C 3. C 4. B 5. C
二、1. △ABE B E
2. A 60° AC
3. 线段、正方形、圆 线段、角、等边三角形、正方形、圆
三、（1）45° （2）60° （3）45° （4）72° （5）30°
四、将（1）先向上平移2格，再向右平移9格，得到（2），将（2）先向左平移1格，再向下平移2 格，然后轴对称得（3）；或将（3）向左平移8格，轴对称得（1），将（2） 向左平移9格，再向下平移2格得（1），等等。
五、如图所示，还有其他移动方式，但都能得到平行四边形，是中心对称图形。
六、1. 108 2. 略 3. 略