1.1 平行线 精品教学课件 (共18张PPT)
文档属性
| 名称 | 1.1 平行线 精品教学课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 13:56:01 | ||
图片预览



文档简介
(共18张PPT)
1.1 平行线
浙教版 七年级下册
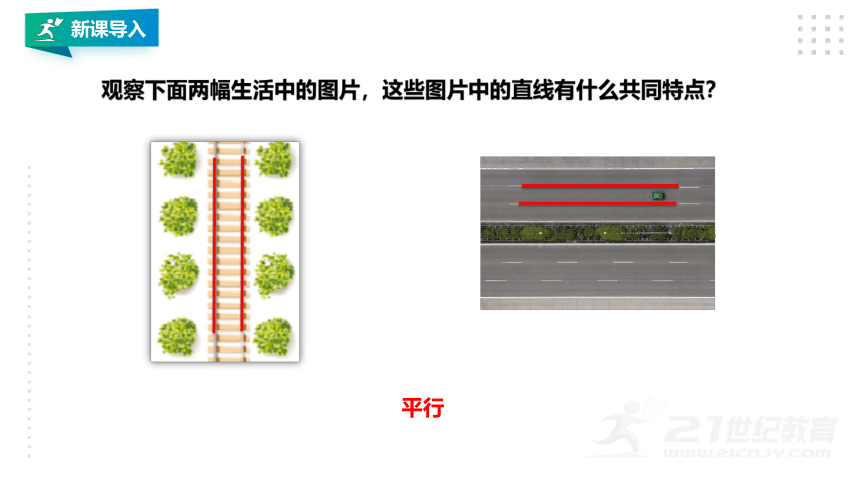
观察下面两幅生活中的图片,这些图片中的直线有什么共同特点?
平行
新课导入
生活中一些其他平行线的例子.
新课导入
A
B
C
D
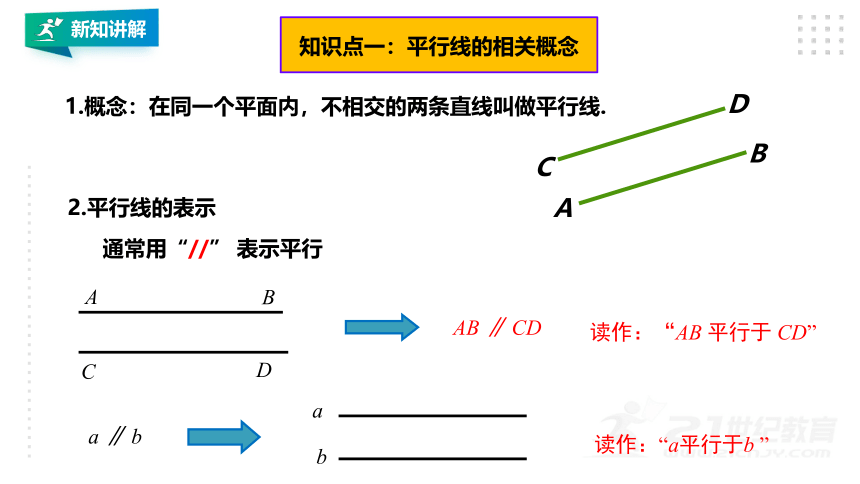
1.概念:在同一个平面内,不相交的两条直线叫做平行线.
知识点一:平行线的相关概念
2.平行线的表示
通常用“//” 表示平行
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
新知讲解
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是两条直线,而不是两条射线或两条线段.
新知讲解
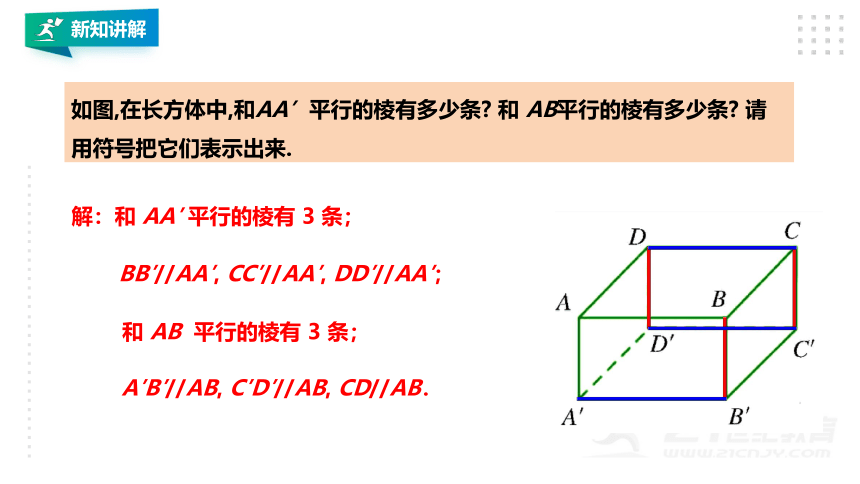
如图,在长方体中,和AA’平行的棱有多少条 和 AB平行的棱有多少条 请用符号把它们表示出来.
解:和 AA′ 平行的棱有 3 条;
BB′//AA′, CC′//AA′, DD′//AA′;
和 AB 平行的棱有 3 条;
A′B′//AB, C′D′//AB, CD//AB.
新知讲解
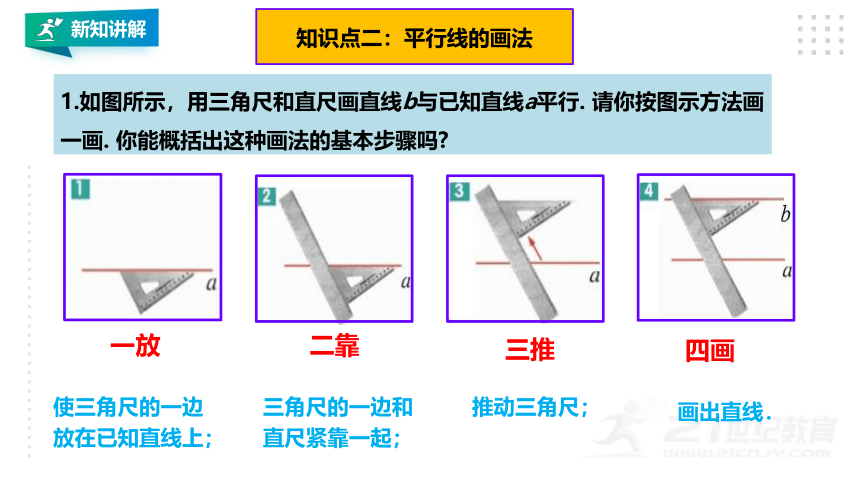
1.如图所示,用三角尺和直尺画直线b与已知直线a平行. 请你按图示方法画一画. 你能概括出这种画法的基本步骤吗
一放
二靠
三推
四画
使三角尺的一边放在已知直线上;
三角尺的一边和直尺紧靠一起;
推动三角尺;
画出直线.
知识点二:平行线的画法
新知讲解
l
无数条
2.已知直线l 和直线外一点P,如图所示.用三角尺和直尺画四条和直线l 平行的直线,并要求其中有直线经过点P.
画已知直线的平行线可以画多少条
过已知直外一点画已知直线的平行线可以画多少条
l
1条
新知讲解
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
几何语言表达式:
∵ a∥n, m∥n (已知)
∴ a∥m (平行线的传递性)
知识点三:平行线的基本事实
新知讲解
例 如图,点M,N 代表两个城市,MA,MB是已建的两条公路.现规划建造两条经N市的公路,这两条公路分别与MB,MA 平行,且在与 MB,MA的交汇处分别建一座立交桥. 问立交桥应建在何处?请画出示意图.
新知讲解
解:如图,过点N分别作直线NP//MA,交MB于点P;
作直线 NQ//MB,交MA于点Q.
所以立交桥应分别建在P,Q处.
新知讲解
D
2.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
C
1.下列表示两条直线平行的方法正确的是( )
A.a∥A B.AB∥cd
C.A∥B D.a∥b
课堂练习
3.下列各说法中正确的是( )
A.两条相交的直线叫做平行线
B.如果a∥b,b∥c,则a不与c平行
C.在直线外一点,只能画出一条直线与已知直线平行
D.两条不平行的射线,在同一平面内一定相交
C
4.下列推理正确的是( )
A.因为a // d,b // c,所以c // d B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c D.因为a // b,c // d,所以a // c
C
课堂练习
5.下列叙述:①在同一平面内,不相交也不重合的两条线段一定平行;
②在同一平面内,射线 a 与射线 b 没有交点,则a∥b;
③若两直线 l1,l2 平行,则 l1 上的线段 AB 与 l2 上的射线 OP 一定平行;④若直线 m 与直线 n 无交点,则 m∥n;
⑤在同一平面内,不平行也不重合的两条直线一定相交.其中正确的个数为( )
A.4 B.3 C.2 D.1
C
课堂练习
解:(1)(2)如图.
6.如图,在∠AOB内有一点P.
(1)过点P作l1∥OA;
(2)过点P作l2∥OB;
课堂练习
课堂小结
概念:在同一个平面内,不相交的两条直线叫做平行线.
表示:AB ∥ CD,a ∥ b
画法: 一放,二靠,三推,四画
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
平行线
https://www.21cnjy.com/help/help_extract.php
1.1 平行线
浙教版 七年级下册
观察下面两幅生活中的图片,这些图片中的直线有什么共同特点?
平行
新课导入
生活中一些其他平行线的例子.
新课导入
A
B
C
D
1.概念:在同一个平面内,不相交的两条直线叫做平行线.
知识点一:平行线的相关概念
2.平行线的表示
通常用“//” 表示平行
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
新知讲解
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是两条直线,而不是两条射线或两条线段.
新知讲解
如图,在长方体中,和AA’平行的棱有多少条 和 AB平行的棱有多少条 请用符号把它们表示出来.
解:和 AA′ 平行的棱有 3 条;
BB′//AA′, CC′//AA′, DD′//AA′;
和 AB 平行的棱有 3 条;
A′B′//AB, C′D′//AB, CD//AB.
新知讲解
1.如图所示,用三角尺和直尺画直线b与已知直线a平行. 请你按图示方法画一画. 你能概括出这种画法的基本步骤吗
一放
二靠
三推
四画
使三角尺的一边放在已知直线上;
三角尺的一边和直尺紧靠一起;
推动三角尺;
画出直线.
知识点二:平行线的画法
新知讲解
l
无数条
2.已知直线l 和直线外一点P,如图所示.用三角尺和直尺画四条和直线l 平行的直线,并要求其中有直线经过点P.
画已知直线的平行线可以画多少条
过已知直外一点画已知直线的平行线可以画多少条
l
1条
新知讲解
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
几何语言表达式:
∵ a∥n, m∥n (已知)
∴ a∥m (平行线的传递性)
知识点三:平行线的基本事实
新知讲解
例 如图,点M,N 代表两个城市,MA,MB是已建的两条公路.现规划建造两条经N市的公路,这两条公路分别与MB,MA 平行,且在与 MB,MA的交汇处分别建一座立交桥. 问立交桥应建在何处?请画出示意图.
新知讲解
解:如图,过点N分别作直线NP//MA,交MB于点P;
作直线 NQ//MB,交MA于点Q.
所以立交桥应分别建在P,Q处.
新知讲解
D
2.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
C
1.下列表示两条直线平行的方法正确的是( )
A.a∥A B.AB∥cd
C.A∥B D.a∥b
课堂练习
3.下列各说法中正确的是( )
A.两条相交的直线叫做平行线
B.如果a∥b,b∥c,则a不与c平行
C.在直线外一点,只能画出一条直线与已知直线平行
D.两条不平行的射线,在同一平面内一定相交
C
4.下列推理正确的是( )
A.因为a // d,b // c,所以c // d B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c D.因为a // b,c // d,所以a // c
C
课堂练习
5.下列叙述:①在同一平面内,不相交也不重合的两条线段一定平行;
②在同一平面内,射线 a 与射线 b 没有交点,则a∥b;
③若两直线 l1,l2 平行,则 l1 上的线段 AB 与 l2 上的射线 OP 一定平行;④若直线 m 与直线 n 无交点,则 m∥n;
⑤在同一平面内,不平行也不重合的两条直线一定相交.其中正确的个数为( )
A.4 B.3 C.2 D.1
C
课堂练习
解:(1)(2)如图.
6.如图,在∠AOB内有一点P.
(1)过点P作l1∥OA;
(2)过点P作l2∥OB;
课堂练习
课堂小结
概念:在同一个平面内,不相交的两条直线叫做平行线.
表示:AB ∥ CD,a ∥ b
画法: 一放,二靠,三推,四画
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
平行线
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
