浙教版七年级下册1.1 平行线 课件(共19张PPT)
文档属性
| 名称 | 浙教版七年级下册1.1 平行线 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 16:49:42 | ||
图片预览




文档简介
(共19张PPT)
笔直的跑道线给我们怎样的数学形象?
1.1 平行线
义务教育课程标准实验教科
浙江版《数学》七年级下册
问题一:你能从这些图
片中找到平行线吗?
问题二:你能从教室中找到平行线吗?
问题三:平行线有什么特征?
1.平行线间的宽度(距离)处处相等。
2.平行线不相交。
问题四:生活中哪些还可以看作平行线呢?
新知导入
双杆
铁轨
看一看,它们有什么共同之处?
扶梯
A
B
C
D
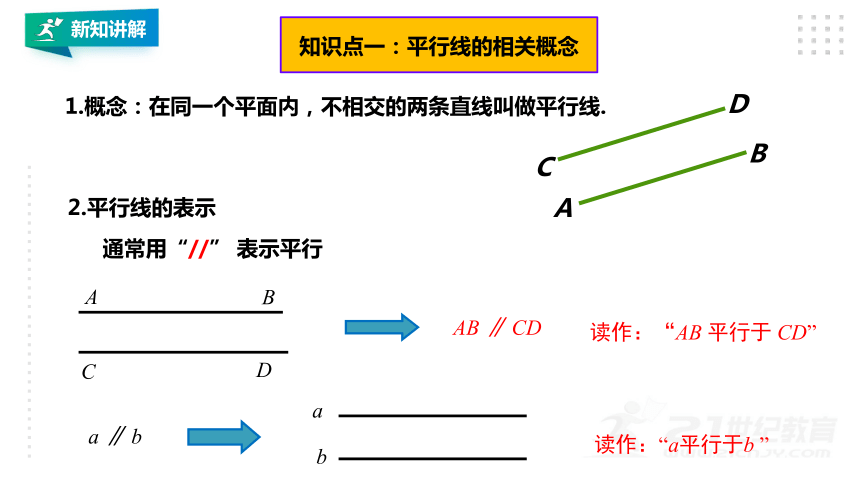
1.概念:在同一个平面内,不相交的两条直线叫做平行线.
知识点一:平行线的相关概念
2.平行线的表示
通常用“//” 表示平行
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
新知讲解
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是两条直线,而不是两条射线或两条线段.
新知讲解
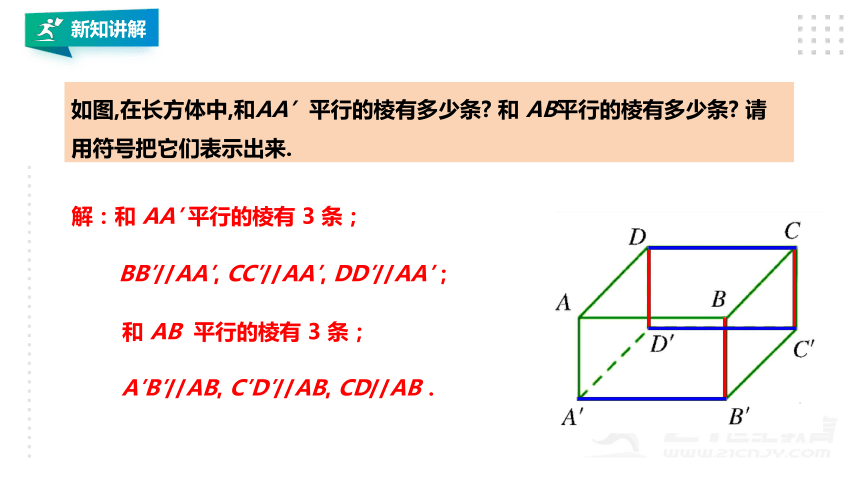
如图,在长方体中,和AA’平行的棱有多少条 和 AB平行的棱有多少条 请用符号把它们表示出来.
解:和 AA′ 平行的棱有 3 条;
BB′//AA′, CC′//AA′, DD′//AA′;
和 AB 平行的棱有 3 条;
A′B′//AB, C′D′//AB, CD//AB.
新知讲解
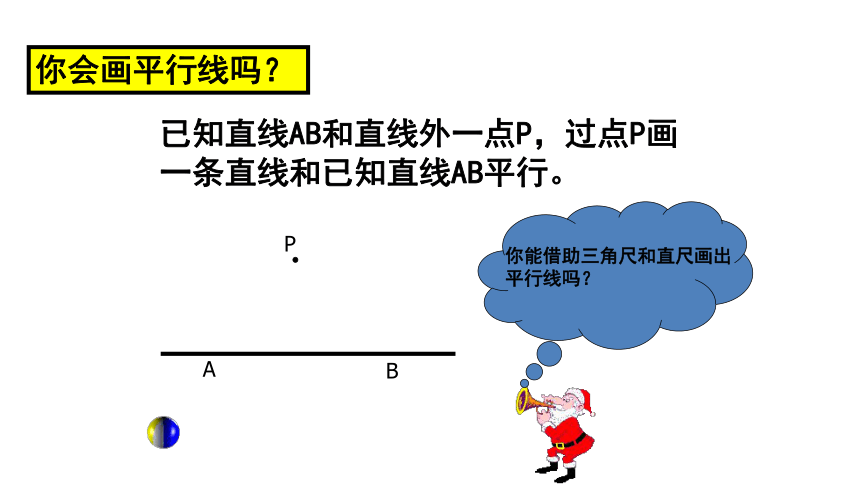
你会画平行线吗?
已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。
A
B
P
你能借助三角尺和直尺画出平行线吗?
例 已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行
A
B
P
画法1:
1.任意画一条直线a,使a⊥AB
a
2.过点P画直线PQ ⊥a
Q
则PQ //AB, PQ就是所要求的直线
平行线的画法
1.如图所示,用三角尺和直尺画直线b与已知直线a平行. 请你按图示方法画一画. 你能概括出这种画法的基本步骤吗
一放
二靠
三推
四画
使三角尺的一边放在已知直线上;
三角尺的一边和直尺紧靠一起;
推动三角尺;
画出直线.
知识点二:平行线的画法
新知讲解
l
无数条
2.已知直线l 和直线外一点P,如图所示.用三角尺和直尺画四条和直线l 平行的直线,并要求其中有直线经过点P.
画已知直线的平行线可以画多少条
过已知直外一点画已知直线的平行线可以画多少条
l
1条
新知讲解
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
几何语言表达式:
∵ a∥n, m∥n (已知)
∴ a∥m (平行线的传递性)
知识点三:平行线的基本事实
新知讲解
例 如图,点M,N 代表两个城市,MA,MB是已建的两条公路.现规划建造两条经N市的公路,这两条公路分别与MB,MA 平行,且在与 MB,MA的交汇处分别建一座立交桥. 问立交桥应建在何处?请画出示意图.
新知讲解
解:如图,过点N分别作直线NP//MA,交MB于点P;
作直线 NQ//MB,交MA于点Q.
所以立交桥应分别建在P,Q处.
新知讲解
D
2.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
C
1.下列表示两条直线平行的方法正确的是( )
A.a∥A B.AB∥cd
C.A∥B D.a∥b
课堂练习
解:(1)(2)如图.
如图,在∠AOB内有一点P.
(1)过点P作l1∥OA;
(2)过点P作l2∥OB;
课堂练习
你学会了吗
1、在同一个平面内, 的两条直线叫做平行线.则在同一个平面内两条不重合直线的位置关系是————.
不相交
2、找出图中各对互相平行的直线。
解:AB ∥CD ∥ FG AD ∥ BC
EH ∥ AG
BD ∥ HI
看谁回答得又对又快!
相交或平行
0个交点
1个交点
2个交点
3个交点
3、同一平面内互不重合的三条直线的交点个数可能是______________________
0 个,1 个,2 个或 3 个
考考你
平面内有若干条直线,当下列情形时,
可将平面最多分成几部分:
(1)有一条直线时,最多分成_____部分。
(2)有两条直线时,最多分成_____部分。
(3)有三条直线时,最多分成_____部分。
(4)有n条直线时,最多分成__________
部分。
2
4
7
n(n+1)
2
——
+1
拓展练习
课堂小结
概念:在同一个平面内,不相交的两条直线叫做平行线.
表示:AB ∥ CD,a ∥ b
画法: 一放,二靠,三推,四画
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
平行线
笔直的跑道线给我们怎样的数学形象?
1.1 平行线
义务教育课程标准实验教科
浙江版《数学》七年级下册
问题一:你能从这些图
片中找到平行线吗?
问题二:你能从教室中找到平行线吗?
问题三:平行线有什么特征?
1.平行线间的宽度(距离)处处相等。
2.平行线不相交。
问题四:生活中哪些还可以看作平行线呢?
新知导入
双杆
铁轨
看一看,它们有什么共同之处?
扶梯
A
B
C
D
1.概念:在同一个平面内,不相交的两条直线叫做平行线.
知识点一:平行线的相关概念
2.平行线的表示
通常用“//” 表示平行
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
新知讲解
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是两条直线,而不是两条射线或两条线段.
新知讲解
如图,在长方体中,和AA’平行的棱有多少条 和 AB平行的棱有多少条 请用符号把它们表示出来.
解:和 AA′ 平行的棱有 3 条;
BB′//AA′, CC′//AA′, DD′//AA′;
和 AB 平行的棱有 3 条;
A′B′//AB, C′D′//AB, CD//AB.
新知讲解
你会画平行线吗?
已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行。
A
B
P
你能借助三角尺和直尺画出平行线吗?
例 已知直线AB和直线外一点P,过点P画一条直线和已知直线AB平行
A
B
P
画法1:
1.任意画一条直线a,使a⊥AB
a
2.过点P画直线PQ ⊥a
Q
则PQ //AB, PQ就是所要求的直线
平行线的画法
1.如图所示,用三角尺和直尺画直线b与已知直线a平行. 请你按图示方法画一画. 你能概括出这种画法的基本步骤吗
一放
二靠
三推
四画
使三角尺的一边放在已知直线上;
三角尺的一边和直尺紧靠一起;
推动三角尺;
画出直线.
知识点二:平行线的画法
新知讲解
l
无数条
2.已知直线l 和直线外一点P,如图所示.用三角尺和直尺画四条和直线l 平行的直线,并要求其中有直线经过点P.
画已知直线的平行线可以画多少条
过已知直外一点画已知直线的平行线可以画多少条
l
1条
新知讲解
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
几何语言表达式:
∵ a∥n, m∥n (已知)
∴ a∥m (平行线的传递性)
知识点三:平行线的基本事实
新知讲解
例 如图,点M,N 代表两个城市,MA,MB是已建的两条公路.现规划建造两条经N市的公路,这两条公路分别与MB,MA 平行,且在与 MB,MA的交汇处分别建一座立交桥. 问立交桥应建在何处?请画出示意图.
新知讲解
解:如图,过点N分别作直线NP//MA,交MB于点P;
作直线 NQ//MB,交MA于点Q.
所以立交桥应分别建在P,Q处.
新知讲解
D
2.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
C
1.下列表示两条直线平行的方法正确的是( )
A.a∥A B.AB∥cd
C.A∥B D.a∥b
课堂练习
解:(1)(2)如图.
如图,在∠AOB内有一点P.
(1)过点P作l1∥OA;
(2)过点P作l2∥OB;
课堂练习
你学会了吗
1、在同一个平面内, 的两条直线叫做平行线.则在同一个平面内两条不重合直线的位置关系是————.
不相交
2、找出图中各对互相平行的直线。
解:AB ∥CD ∥ FG AD ∥ BC
EH ∥ AG
BD ∥ HI
看谁回答得又对又快!
相交或平行
0个交点
1个交点
2个交点
3个交点
3、同一平面内互不重合的三条直线的交点个数可能是______________________
0 个,1 个,2 个或 3 个
考考你
平面内有若干条直线,当下列情形时,
可将平面最多分成几部分:
(1)有一条直线时,最多分成_____部分。
(2)有两条直线时,最多分成_____部分。
(3)有三条直线时,最多分成_____部分。
(4)有n条直线时,最多分成__________
部分。
2
4
7
n(n+1)
2
——
+1
拓展练习
课堂小结
概念:在同一个平面内,不相交的两条直线叫做平行线.
表示:AB ∥ CD,a ∥ b
画法: 一放,二靠,三推,四画
基本事实:
经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
平行线
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
