2021—2022学年浙教版七年级数学下册3.4.2完全平方公式 同步练习 (word版含答案)
文档属性
| 名称 | 2021—2022学年浙教版七年级数学下册3.4.2完全平方公式 同步练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 69.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 00:00:00 | ||
图片预览



文档简介
3.4 第2课时 完全平方公式
知识点 1 完全平方公式
1.根据完全平方公式填空:
(1)(x+1)2=( )2+2× × +( )2= ;
(2)(-x+1)2=( )2+2× × +( )2= ;
(3)(-2a-b)2=( )2+2× × +( )2= .
2.计算(1-x)2的结果为 ( )
A.1-x2 B.1+x2
C.1-2x+x2 D.1+2x+x2
3.边长为m的正方形的边长增加n以后,所得新正方形的面积比原正方形的面积增加了 ( )
A.n2 B.2mn
C.2mn-n2 D.2mn+n2
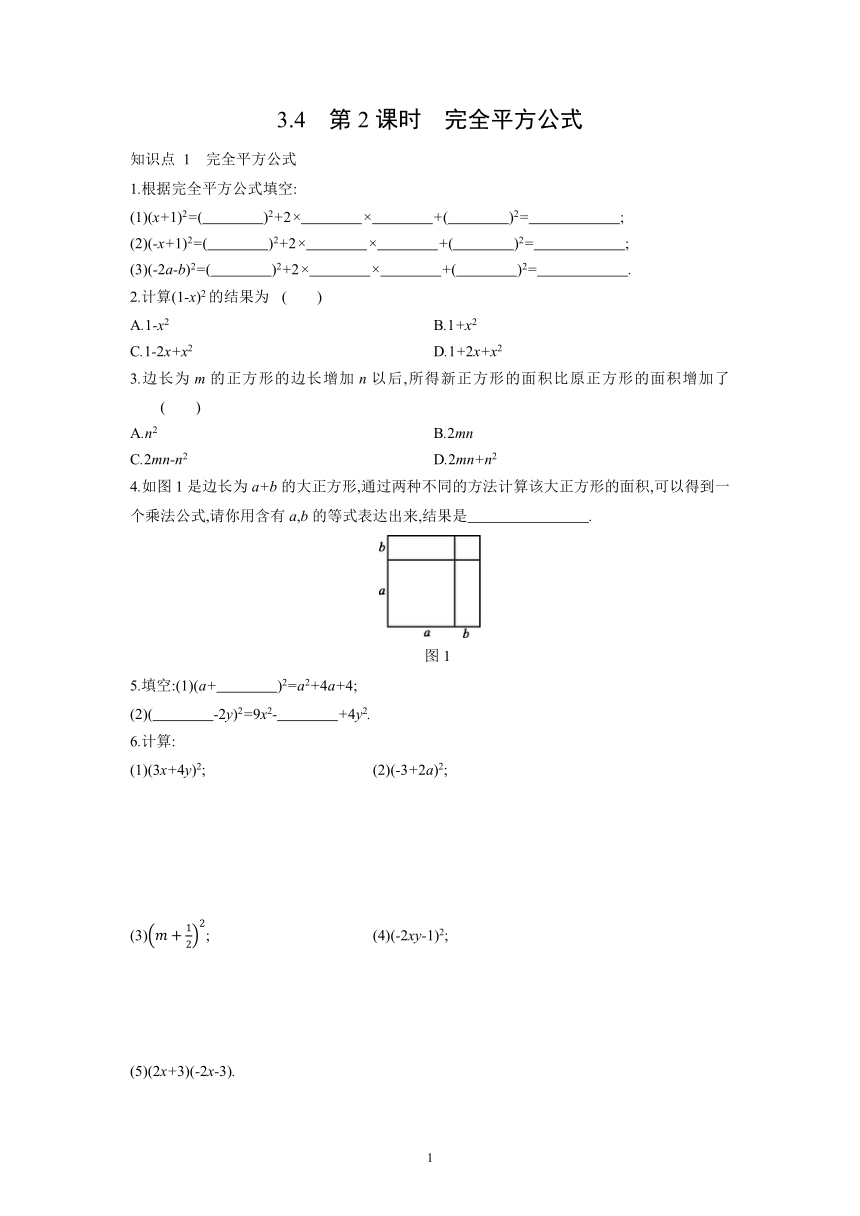
4.如图1是边长为a+b的大正方形,通过两种不同的方法计算该大正方形的面积,可以得到一个乘法公式,请你用含有a,b的等式表达出来,结果是 .
图1
5.填空:(1)(a+ )2=a2+4a+4;
(2)( -2y)2=9x2- +4y2.
6.计算:
(1)(3x+4y)2; (2)(-3+2a)2;
(3); (4)(-2xy-1)2;
(5)(2x+3)(-2x-3).
知识点 2 利用完全平方公式简便运算
7.计算1202-40×120+202的结果为 ( )
A.10000 B.1200 C.800 D.22500
8.计算:(1)9992;
(2)992-198×100+1002.
【能力提升】
9.若(x+2y)2=(x-2y)2+A,则A为 ( )
A.8xy B.-8xy C.8y2 D.4xy
10.形如a2+2ab+b2和a2-2ab+b2的式子称为完全平方式.若x2+ax+4(a为常数)是一个完全平方式,则a等于 ( )
A.2 B.4 C.±2 D.±4
11.如图2,有5张边长为2的正方形纸片,4张长、宽分别为3和2的长方形纸片,6张边长为3的正方形纸片,若从中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个新的正方形(原纸张进行无空隙、无重叠拼接),则拼成的新的正方形的最大边长为 ( )
图2
A.6 B.7 C.8 D.9
12.已知a-b=7,ab=2,则(a+b)2= .
13.计算:
(1)(x+y)2-2xy;
(2)a(a-2b)+(a+b)2.
14.运用完全平方公式计算:(2x-2)2+(3x+1)2.
15.计算:
(1)(3x+2)2(3x-2)2;
(2)29×31×(302+1).
16.我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:(a+b)(a+2b)=a2+3ab+2b2,就可以用图3①所示的图形面积关系来说明.
(1)请根据图②写出代数恒等式,并根据所写恒等式计算:(2x-y-3)2;
(2)若x2+y2+z2=1,xy+yz+xz=4,求x+y+z的值;
(3)现有如图③所示的卡片:A型、B型、C型,把这些卡片不重叠、不留缝隙地贴在棱长为(a+b)的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需费用多少元
图3
答案
1.(1)x x 1 1 x2+2x+1
(2)-x (-x) 1 1 x2-2x+1
(3)-2a (-2a) (-b) -b 4a2+4ab+b2
2.C
3.D
4.(a+b)2=a2+2ab+b2
5.(1)2 (2)3x 12xy
6.(1)9x2+24xy+16y2
(2)4a2-12a+9
(3)m2+m+
(4)4x2y2+4xy+1
(5)-4x2-12x-9
7.A
8.解:(1)9992=(1000-1)2=10002-2×1000×1+12=998001.
(2)原式=992-2×99×100+1002
=(99-100)2
=1.
9.A .
10.D
11.D
12.57
13.解:(1)原式=x2+2xy+y2-2xy=x2+y2.
(2)a(a-2b)+(a+b)2
=a2-2ab+a2+2ab+b2
=2a2+b2.
14.解:(2x-2)2+(3x+1)2
=4x2-8x+4+9x2+6x+1
=13x2-2x+5.
15.解:(1)原式=(9x2-4)2=81x4-72x2+16.
(2)原式=(30-1)(30+1)(302+1)=304-1=809999.
16.解:(1)原题图②中,大正方形的面积=3个小正方形的面积+6个小长方形的面积,
因此有(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
所以(2x-y-3)2=4x2+y2+9-4xy-12x+6y.
(2)因为xy+yz+xz=4,
所以2xy+2yz+2xz=8,
所以(x+y+z)2=x2+y2+z2+2xy+2yz+2xz=9,
所以x+y+z=±3.
(3)棱长为(a+b)的100个立方体的表面积是
100×6×(a+b)2=600a2+600b2+1200ab.
题图中A型卡片是正方形,面积是a2,B型卡片是长方形,面积是ab,C型卡片是正方形,面积是b2,
所以需要600张A型卡片,600张C型卡片,1200张B型卡片,
所需费用为600×0.7+600×0.4+1200×0.5=1260(元).
(
1
)
知识点 1 完全平方公式
1.根据完全平方公式填空:
(1)(x+1)2=( )2+2× × +( )2= ;
(2)(-x+1)2=( )2+2× × +( )2= ;
(3)(-2a-b)2=( )2+2× × +( )2= .
2.计算(1-x)2的结果为 ( )
A.1-x2 B.1+x2
C.1-2x+x2 D.1+2x+x2
3.边长为m的正方形的边长增加n以后,所得新正方形的面积比原正方形的面积增加了 ( )
A.n2 B.2mn
C.2mn-n2 D.2mn+n2
4.如图1是边长为a+b的大正方形,通过两种不同的方法计算该大正方形的面积,可以得到一个乘法公式,请你用含有a,b的等式表达出来,结果是 .
图1
5.填空:(1)(a+ )2=a2+4a+4;
(2)( -2y)2=9x2- +4y2.
6.计算:
(1)(3x+4y)2; (2)(-3+2a)2;
(3); (4)(-2xy-1)2;
(5)(2x+3)(-2x-3).
知识点 2 利用完全平方公式简便运算
7.计算1202-40×120+202的结果为 ( )
A.10000 B.1200 C.800 D.22500
8.计算:(1)9992;
(2)992-198×100+1002.
【能力提升】
9.若(x+2y)2=(x-2y)2+A,则A为 ( )
A.8xy B.-8xy C.8y2 D.4xy
10.形如a2+2ab+b2和a2-2ab+b2的式子称为完全平方式.若x2+ax+4(a为常数)是一个完全平方式,则a等于 ( )
A.2 B.4 C.±2 D.±4
11.如图2,有5张边长为2的正方形纸片,4张长、宽分别为3和2的长方形纸片,6张边长为3的正方形纸片,若从中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个新的正方形(原纸张进行无空隙、无重叠拼接),则拼成的新的正方形的最大边长为 ( )
图2
A.6 B.7 C.8 D.9
12.已知a-b=7,ab=2,则(a+b)2= .
13.计算:
(1)(x+y)2-2xy;
(2)a(a-2b)+(a+b)2.
14.运用完全平方公式计算:(2x-2)2+(3x+1)2.
15.计算:
(1)(3x+2)2(3x-2)2;
(2)29×31×(302+1).
16.我们知道:有些代数恒等式可以利用平面图形的面积来表示,如:(a+b)(a+2b)=a2+3ab+2b2,就可以用图3①所示的图形面积关系来说明.
(1)请根据图②写出代数恒等式,并根据所写恒等式计算:(2x-y-3)2;
(2)若x2+y2+z2=1,xy+yz+xz=4,求x+y+z的值;
(3)现有如图③所示的卡片:A型、B型、C型,把这些卡片不重叠、不留缝隙地贴在棱长为(a+b)的100个立方体表面进行装饰,A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张,共需费用多少元
图3
答案
1.(1)x x 1 1 x2+2x+1
(2)-x (-x) 1 1 x2-2x+1
(3)-2a (-2a) (-b) -b 4a2+4ab+b2
2.C
3.D
4.(a+b)2=a2+2ab+b2
5.(1)2 (2)3x 12xy
6.(1)9x2+24xy+16y2
(2)4a2-12a+9
(3)m2+m+
(4)4x2y2+4xy+1
(5)-4x2-12x-9
7.A
8.解:(1)9992=(1000-1)2=10002-2×1000×1+12=998001.
(2)原式=992-2×99×100+1002
=(99-100)2
=1.
9.A .
10.D
11.D
12.57
13.解:(1)原式=x2+2xy+y2-2xy=x2+y2.
(2)a(a-2b)+(a+b)2
=a2-2ab+a2+2ab+b2
=2a2+b2.
14.解:(2x-2)2+(3x+1)2
=4x2-8x+4+9x2+6x+1
=13x2-2x+5.
15.解:(1)原式=(9x2-4)2=81x4-72x2+16.
(2)原式=(30-1)(30+1)(302+1)=304-1=809999.
16.解:(1)原题图②中,大正方形的面积=3个小正方形的面积+6个小长方形的面积,
因此有(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
所以(2x-y-3)2=4x2+y2+9-4xy-12x+6y.
(2)因为xy+yz+xz=4,
所以2xy+2yz+2xz=8,
所以(x+y+z)2=x2+y2+z2+2xy+2yz+2xz=9,
所以x+y+z=±3.
(3)棱长为(a+b)的100个立方体的表面积是
100×6×(a+b)2=600a2+600b2+1200ab.
题图中A型卡片是正方形,面积是a2,B型卡片是长方形,面积是ab,C型卡片是正方形,面积是b2,
所以需要600张A型卡片,600张C型卡片,1200张B型卡片,
所需费用为600×0.7+600×0.4+1200×0.5=1260(元).
(
1
)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
