1.3 平行线的判定 同步练习（含解析）

中小学教育资源及组卷应用平台
浙教版七年级下 1.3平行线的判定同步练习
一．选择题
1．（2021秋 文山市期末）下列图形中，由∠1＝∠2能得到AB∥CD的是（　　）
A．B． C．D．
2．（2020秋 盐田区期末）如图，点E在射线AB上，要AD∥BC，只需（　　）
A．∠A＝∠CBE B．∠A＝∠C C．∠C＝∠CBE D．∠A+∠D＝180°
3．（2021秋 于洪区期末）如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（　　）
A．∠1＝∠3 B．∠2+∠3＝180° C．∠1＝∠4 D．∠1+∠4＝180°
4．（2021秋 肇源县期末）如图，下列能判定AB∥CD的条件有（　　）个．
（1）∠B+∠BCD＝180°；（2）∠1＝∠2；（3）∠3＝∠4；（4）∠B＝∠5．
A．1 B．2 C．3 D．4
5．（2020春 岳西县期末）有下列说法：①对顶角相等；②内错角相等；③平面内过一点有且只有一条直线垂直于已知直线；④平面内过一点有且只有一条直线平行于已知直线，其中正确的结论有（　　）个．
A．1 B．2 C．3 D．4
6．（2021春 柳南区校级期末）如图，下面哪个条件不能判断AC∥EF的是（　　）
A．∠1＝∠2 B．∠4＝∠C C．∠1+∠3＝180° D．∠3+∠C＝180°
7．（2021春 孟村县期末）木工师傅用图中的角尺画平行线，他依据的数学道理是（　　）
A．同位角相等，两直线平行 B．内错角相等，两直线平行
C．同旁内角互补，两直线平行 D．以上结论都不正确
8．（2021 香坊区校级开学）如图，下列条件中能判定AB∥CD的是（　　）
A．∠AEC＝∠BFD B．∠CEF＝∠BFE C．∠AEF+∠CFE＝180° D．∠C＝∠BFD
9．（2021春 高州市月考）如图所示，已知直线c与a，b分别交于点A、B且∠1＝120°，当∠2＝（　　）时，直线a∥b．
A．60° B．120° C．30° D．150°
10．（2021春 瑶海区期末）下列说法中，错误的是（　　）
A．平面内，过一点有且只有一条直线垂直于已知直线
B．在连接直线外一点与直线上各点的线段中，垂线最短
C．经过直线外一点，有且只有一条直线平行于这条直线
D．同位角相等，两直线平行
二．填空题
11．（2021 桂林）如图，直线a，b被直线c所截，当∠1 　 　∠2时，a∥b．（用“＞”，“＜”或“＝”填空）
12．（2021春 思明区校级月考）结合图（不能自己标角），用符号语言表达“同旁内角互补，两直线平行”的推理形式：
∵　 　，
∴　 　．
13．（2021春 兴宾区期末）如图，将两个含30°角的直角三角板的最长边靠在一起滑动，可知直角边AB∥CD，依据是　 　．
14．（2021秋 杜尔伯特县期末）如图，不添加辅助线，请写出一个能判定AD∥BC的条件 　 　．
15．（2021春 呼和浩特期末）如图，下列条件中：①∠B+∠BCD＝180°；②∠1＝∠2；③∠3＝∠4；④∠B＝∠5．能判定AB∥CD的条件为 　 　．
16．（2020春 夏邑县期末）将一块三角板ABC（∠BAC＝90°，∠ABC＝30°）按如图方式放置，使A，B两点分别落在直线m，n上．对于给出的四个条件：①∠1＝25.5°，∠2＝55°30'；②∠2＝2∠1；③∠1+∠2＝90°；④∠ACB＝∠1+∠2；⑤∠ABC＝∠2﹣∠1．能判断直线m∥n的有　 　．（填序号）
三．解答题
17．（2021秋 杜尔伯特县期末）完成下面的证明：已知：如图，∠1＝30°，∠B＝60°，AB⊥AC．求证：AD∥BC．
证明：∵AB⊥AC（已知），
∴∠　 　＝90° （ 　 　），
∵∠1＝30°，∠B＝60°（已知），
∴∠1+∠BAC+∠B＝　 　（ 　 　），
即∠　 　+∠B＝180°，
∴AD∥BC （ 　 　）．
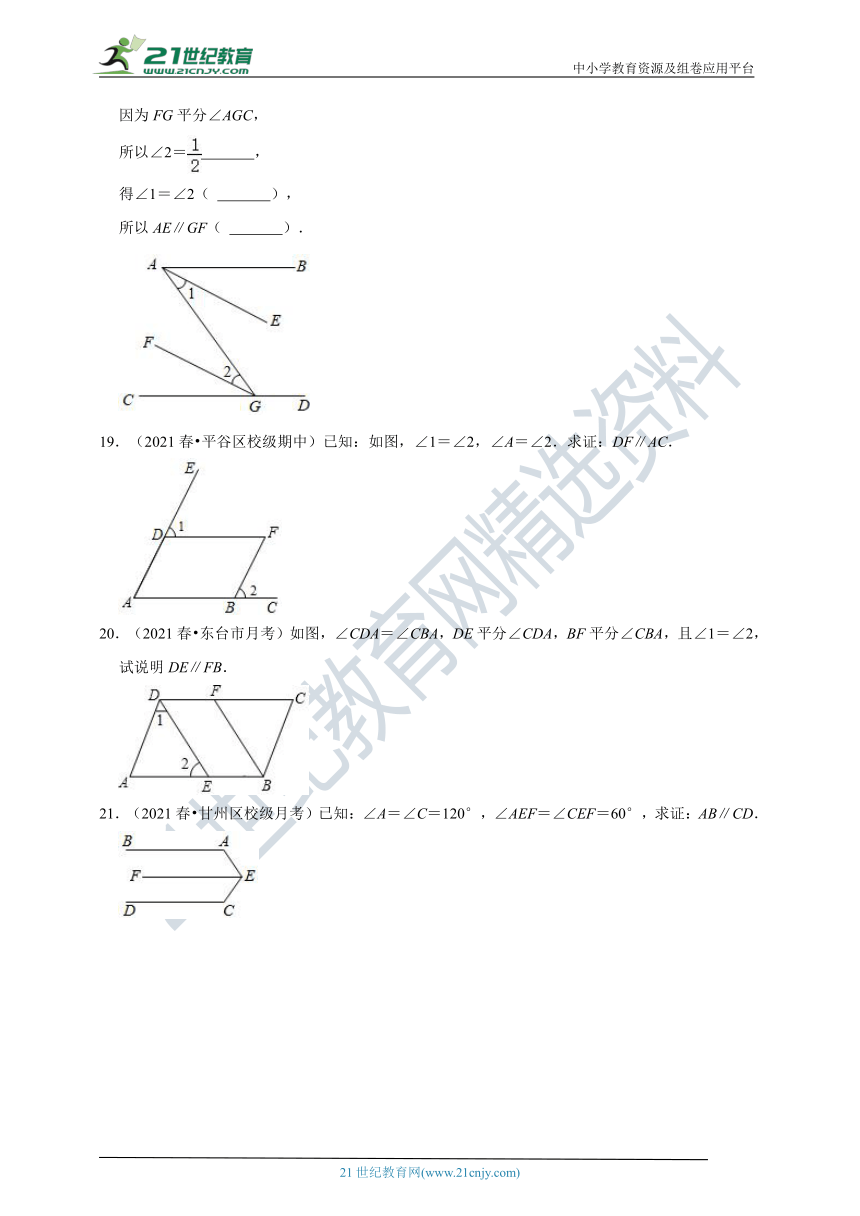
18．（2021春 普陀区校级月考）如图，点G在CD上，已知∠BAG+∠AGD＝180°，EA平分∠BAG，FG平分∠AGC，请说明AE∥GF的理由．
解：因为∠BAG+∠AGD＝180°（ 　 　），
∠AGC+∠AGD＝180°（ 　 　），
所以∠BAG＝∠AGC（ 　 　）．
因为EA平分∠BAG，
所以∠1＝　 　（ 　 　）．
因为FG平分∠AGC，
所以∠2＝　 　，
得∠1＝∠2（ 　 　），
所以AE∥GF（ 　 　）．
19．（2021春 平谷区校级期中）已知：如图，∠1＝∠2，∠A＝∠2．求证：DF∥AC．
20．（2021春 东台市月考）如图，∠CDA＝∠CBA，DE平分∠CDA，BF平分∠CBA，且∠1＝∠2，试说明DE∥FB．
21．（2021春 甘州区校级月考）已知：∠A＝∠C＝120°，∠AEF＝∠CEF＝60°，求证：AB∥CD．
答案与解析
一．选择题
1．（2021秋 文山市期末）下列图形中，由∠1＝∠2能得到AB∥CD的是（　　）
A．B． C．D．
【解析】解：A、∠1＝∠2，AB∥CD，符合题意；
B、∠1+∠2＝180°，AB∥CD，不符合题意；
C、∠1＝∠2，得不出AB∥CD，不符合题意；
D、∠1＝∠2，得不出AB∥CD，不符合题意；
故选：A．
2．（2020秋 盐田区期末）如图，点E在射线AB上，要AD∥BC，只需（　　）
A．∠A＝∠CBE B．∠A＝∠C C．∠C＝∠CBE D．∠A+∠D＝180°
【解析】解：要AD∥BC，只需∠A＝∠CBE，
故选：A．
3．（2021秋 于洪区期末）如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（　　）
A．∠1＝∠3 B．∠2+∠3＝180° C．∠1＝∠4 D．∠1+∠4＝180°
【解析】解：A、当∠1＝∠3时，有a∥b，故A不符合题意；
B、当∠2+∠3＝180°时，有a∥b，故B不符合题意；
C、当∠1＝∠4时，
∵∠3＝∠4，
∴∠1＝∠3，
∴a∥b，故C不符合题意；
D、当∠1+∠4＝180°时，不能判定a∥b，故D符合题意．
故选：D．
4．（2021秋 肇源县期末）如图，下列能判定AB∥CD的条件有（　　）个．
（1）∠B+∠BCD＝180°；（2）∠1＝∠2； （3）∠3＝∠4；（4）∠B＝∠5．
A．1 B．2 C．3 D．4
【解析】解：（1）利用同旁内角互补，判定两直线平行，故（1）正确；
（2）利用内错角相等，判定两直线平行，∵∠1＝∠2，∴AD∥BC，而不能判定AB∥CD，故（2）错误；
（3）利用内错角相等，判定两直线平行，故（3）正确；
（4）利用同位角相等，判定两直线平行，故（4）正确．
故选：C．
5．（2020春 岳西县期末）有下列说法：①对顶角相等；②内错角相等；③平面内过一点有且只有一条直线垂直于已知直线；④平面内过一点有且只有一条直线平行于已知直线，其中正确的结论有（　　）个．
A．1 B．2 C．3 D．4
【解析】解：①对顶角相等是正确的；
②内错角相等不一定相等，原来的说法错误；
③平面内过一点有且只有一条直线垂直于已知直线是正确的；
④平面内过直线外一点有且只有一条直线平行于已知直线，原来的说法错误．
故选：B．
6．（2021春 柳南区校级期末）如图，下面哪个条件不能判断AC∥EF的是（　　）
A．∠1＝∠2 B．∠4＝∠C C．∠1+∠3＝180° D．∠3+∠C＝180°
【解析】解：当∠1＝∠2时，AC∥EF，故选项A不符合题意；
当∠4＝∠C时，AC∥EF，故选项B不符合题意；
当∠1+∠3＝180°时，BC∥DE，不能判断AC∥EF，故选项C符合题意；
当∠3+∠C＝180°时，AC∥EF，故选项D不符合题意；
故选：C．
7．（2021春 孟村县期末）木工师傅用图中的角尺画平行线，他依据的数学道理是（　　）
A．同位角相等，两直线平行 B．内错角相等，两直线平行
C．同旁内角互补，两直线平行 D．以上结论都不正确
【解析】解：木工师傅用图中的角尺画平行线，他依据的数学道理是同位角相等，两直线平行，
故选：A．
8．（2021 香坊区校级开学）如图，下列条件中能判定AB∥CD的是（　　）
A．∠AEC＝∠BFD B．∠CEF＝∠BFE C．∠AEF+∠CFE＝180° D．∠C＝∠BFD
【解析】解：A．由∠AEC＝∠BFD，不能判定AB∥CD，故本选项不符合题意；
B．由∠CEF＝∠BFE，可判定CE∥BF，不能判定AB∥CD，故本选项不符合题意；
C．由∠AEF+∠CFE＝180°，根据“同旁内角互补，两直线平行”能判定AB∥CD，故本选项符合题意；
D．由∠C＝∠BFD，可判定CE∥BF，不能判定AB∥CD，故本选项不符合题意；
故选：C．
9．（2021春 高州市月考）如图所示，已知直线c与a，b分别交于点A、B且∠1＝120°，当∠2＝（　　）时，直线a∥b．
A．60° B．120° C．30° D．150°
【解析】解：∵∠1＝120°，∠1与∠3是对顶角，
∴∠1＝∠3＝120°，
∵∠2＝∠3＝120°，
∴直线a∥b，
故选：B．
10．（2021春 瑶海区期末）下列说法中，错误的是（　　）
A．平面内，过一点有且只有一条直线垂直于已知直线
B．在连接直线外一点与直线上各点的线段中，垂线最短
C．经过直线外一点，有且只有一条直线平行于这条直线
D．同位角相等，两直线平行
【解析】解：A．在同一平面内，过一点有且只有一条直线垂直于已知直线，该选项说法正确，故该选项不符合题意；
B．在连接直线外一点与直线上各点的线段中，垂线段最短，该选项说法错误，故该选项符合题意；
C．经过直线外一点，有且只有一条直线平行于这条直线，该选项说法正确，故该选项不符合题意；
D．同位角相等，两直线平行，该选项说法正确，故该选项不符合题意；
故选：B．
二．填空题
11．（2021 桂林）如图，直线a，b被直线c所截，当∠1 　＝　∠2时，a∥b．（用“＞”，“＜”或“＝”填空）
【解析】解：要使a∥b，只需∠1＝∠2．
即当∠1＝∠2时，
a∥b（同位角相等，两直线平行）．
故答案为＝．
12．（2021春 思明区校级月考）结合图（不能自己标角），用符号语言表达“同旁内角互补，两直线平行”的推理形式：
∵　∠2+∠4＝180°　，
∴　a∥b　．
【解析】解：∵∠2+∠4＝180°，
∴a∥b（同旁内角互补，两直线平行）．
故答案为：∠2+∠4＝180°；a∥b．
13．（2021春 兴宾区期末）如图，将两个含30°角的直角三角板的最长边靠在一起滑动，可知直角边AB∥CD，依据是　内错角相等，两直线平行　．
【解析】解：如图所示：
∵∠1＝∠2＝30°，
∴AB∥CD（内错角相等，两直线平行），
故答案为：内错角相等，两直线平行．
14．（2021秋 杜尔伯特县期末）如图，不添加辅助线，请写出一个能判定AD∥BC的条件 　∠EAD＝∠B或∠DAC＝∠C或∠DAB+∠B＝180°　．
【解析】解：∵AD和BC被BE所截，
∴当∠EAD＝∠B时，AD∥BC，
或当∠DAC＝∠C时，AD∥BC，
或当∠DAB+∠B＝180°时，AD∥BC，
故答案为：∠EAD＝∠B或∠DAC＝∠C或∠DAB+∠B＝180°．
15．（2021春 呼和浩特期末）如图，下列条件中：①∠B+∠BCD＝180°；②∠1＝∠2；③∠3＝∠4；④∠B＝∠5．能判定AB∥CD的条件为 　①③④　．
【解析】解：①∠B+∠BCD＝180°，同旁内角互补，两直线平行，则能判定AB∥CD；
②∠1＝∠2，但∠1，∠2不是截AB、CD所得的内错角，所不能判定AB∥CD；
③∠3＝∠4，内错角相等，两直线平行，则能判定AB∥CD；
④∠B＝∠5，同位角相等，两直线平行，则能判定AB∥CD．
故能判定AB∥CD的条件为①③④．
故答案为：①③④．
16．（2020春 夏邑县期末）将一块三角板ABC（∠BAC＝90°，∠ABC＝30°）按如图方式放置，使A，B两点分别落在直线m，n上．对于给出的四个条件：①∠1＝25.5°，∠2＝55°30'；②∠2＝2∠1；③∠1+∠2＝90°；④∠ACB＝∠1+∠2；⑤∠ABC＝∠2﹣∠1．能判断直线m∥n的有　①⑤　．（填序号）
【解析】解：①∵∠1＝25.5°，∠ABC＝30°，
∴∠2＝∠1+∠ABC＝55.5°＝55°30'，所以，m∥n；
②没有指明∠1的度数，当∠1≠30°，∠2≠∠1+30°，不能判断直线m∥n，故∠2＝2∠1，不能判断直线m∥n；
③∠1+∠2＝90°，不能判断直线m∥n；
④∠ACB＝∠1+∠2，不能判断直线m∥n；
⑤∠ABC＝∠2﹣∠1，判断直线m∥n；
故答案为：①⑤
三．解答题
17．（2021秋 杜尔伯特县期末）完成下面的证明：已知：如图，∠1＝30°，∠B＝60°，AB⊥AC．求证：AD∥BC．
证明：∵AB⊥AC（已知），
∴∠　BAC　＝90° （ 　垂直的定义　），
∵∠1＝30°，∠B＝60°（已知），
∴∠1+∠BAC+∠B＝　180°　（ 　等量关系　），
即∠　BAD　+∠B＝180°，
∴AD∥BC （ 　同旁内角互补，两直线平行　）．
【解析】解：证明：∵AB⊥AC（已知），
∴∠BAC＝90° （垂直的定义），
∵∠1＝30°，∠B＝60°（已知），
∴∠1+∠BAC+∠B＝180°（等量关系），
即∠BAD+∠B＝180°，
∴AD∥BC （同旁内角互补，两直线平行），
故答案为：BAC；垂直的定义；180°；等量关系；BAD；同旁内角互补，两直线平行．
18．（2021春 普陀区校级月考）如图，点G在CD上，已知∠BAG+∠AGD＝180°，EA平分∠BAG，FG平分∠AGC，请说明AE∥GF的理由．
解：因为∠BAG+∠AGD＝180°（ 　已知　），
∠AGC+∠AGD＝180°（ 　邻补角的定义　），
所以∠BAG＝∠AGC（ 　同角的补角相等　）．
因为EA平分∠BAG，
所以∠1＝　∠BAG　（ 　角平分线的定义　）．
因为FG平分∠AGC，
所以∠2＝　∠AGC　，
得∠1＝∠2（ 　等量代换　），
所以AE∥GF（ 　内错角相等，两直线平行　）．
【解析】解：因为∠BAG+∠AGD＝180°（已知），
∠AGC+∠AGD＝180°（邻补角的定义），
所以∠BAG＝∠AGC（同角的补角相等），
因为EA平分∠BAG，
所以∠1＝∠BAG（角平分线的定义），
因为FG平分∠AGC，
所以∠2＝∠AGC，
得∠1＝∠2（等量代换），
所以AE∥GF（内错角相等，两直线平行）．
故答案为：已知；邻补角的定义；同角的补角相等；∠BAG；角平分线的定义；∠AGC；等量代换；内错角相等，两直线平行．
19．（2021春 平谷区校级期中）已知：如图，∠1＝∠2，∠A＝∠2．求证：DF∥AC．
【解析】证明：∵∠1＝∠2，∠A＝∠2，
∴∠1＝∠A，
∴DF∥AC．
20．（2021春 东台市月考）如图，∠CDA＝∠CBA，DE平分∠CDA，BF平分∠CBA，且∠1＝∠2，试说明DE∥FB．
【解析】解：DE∥BF，
理由是：∵∠CDA＝∠CBA，DE平分∠CDA，BF平分∠CBA，
∴∠1＝∠ABF，
∵∠1＝∠2，
∴∠2＝∠ABF，
∴DE∥BF．
21．（2021春 甘州区校级月考）已知：∠A＝∠C＝120°，∠AEF＝∠CEF＝60°，求证：AB∥CD．
【解析】证明：∵∠A＝∠C＝120°，∠AEF＝∠CEF＝60°，
∴∠A+∠AEF＝180°，∠C+∠CEF＝180°，
∴AB∥EF，CD∥EF，
∴AB∥CD．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)