1.4 平行线的性质(2)课件(共18张PPT)
文档属性
| 名称 | 1.4 平行线的性质(2)课件(共18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
1.4 平行线的性质(2)
浙教版 七年级下册
新知导入
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
应用格式:
∴∠1=∠2
(两直线平行,同位角相等)
∵a ∥ b(已知)
b
1
2
a
c
平行线的性质1:
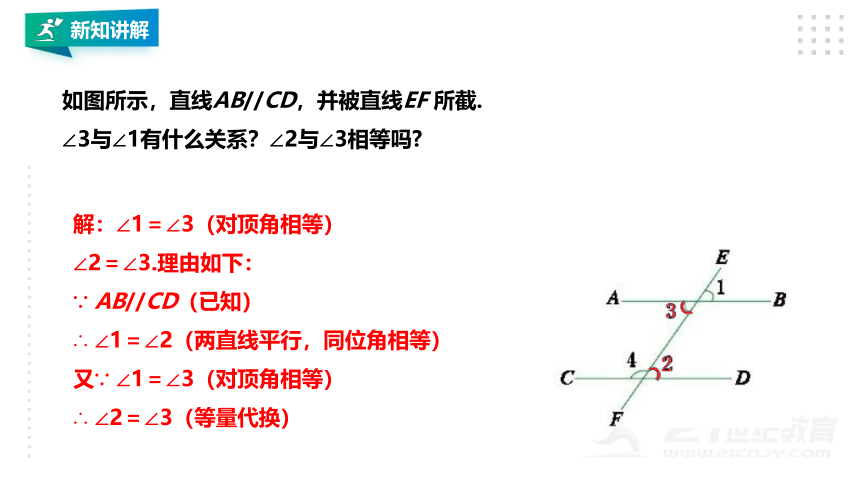
如图所示,直线AB//CD,并被直线EF 所截.
∠3与∠1有什么关系?∠2与∠3相等吗
解:∠1=∠3(对顶角相等)
∠2=∠3.理由如下:
∵ AB//CD(已知)
∴ ∠1=∠2(两直线平行,同位角相等)
又∵ ∠1=∠3(对顶角相等)
∴ ∠2=∠3(等量代换)
新知讲解
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简单说成,两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等).
∵a∥b(已知),
应用格式:
新知讲解
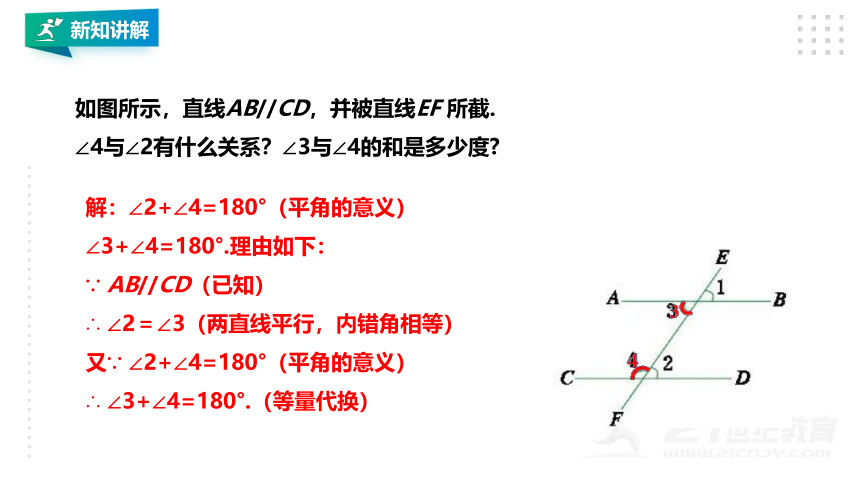
如图所示,直线AB//CD,并被直线EF 所截.
∠4与∠2有什么关系?∠3与∠4的和是多少度
解:∠2+∠4=180°(平角的意义)
∠3+∠4=180°.理由如下:
∵ AB//CD(已知)
∴ ∠2=∠3(两直线平行,内错角相等)
又∵ ∠2+∠4=180°(平角的意义)
∴ ∠3+∠4=180°.(等量代换)
新知讲解
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简单说成,两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补).
∵a∥b(已知),
应用格式:
新知讲解
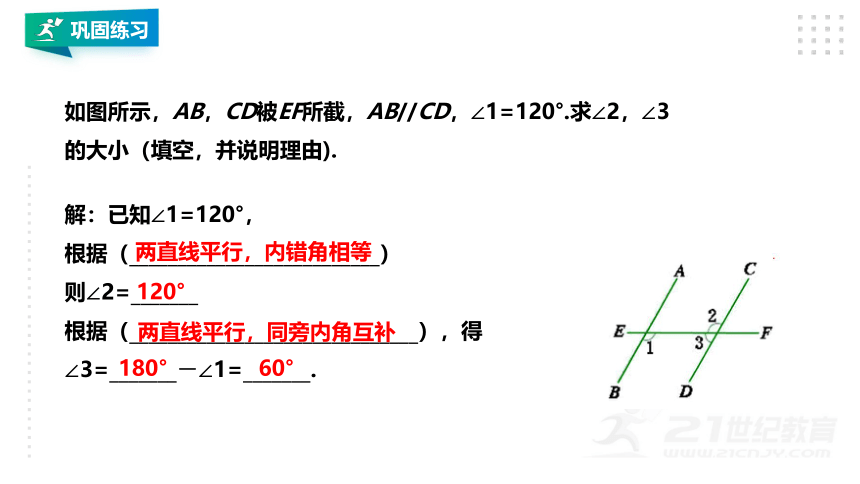
如图所示,AB,CD被EF所截,AB//CD,∠1=120°.求∠2,∠3的大小(填空,并说明理由).
解:已知∠1=120°,
根据(__________________________)
则∠2=_______
根据(______________________________),得
∠3=_______-∠1=_______.
两直线平行,内错角相等
120°
两直线平行,同旁内角互补
180°
60°
巩固练习
(1)两直线平行,同位角相等.
几何语言:
∵ AB//CD (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
(2)两直线平行,内错角相等.
几何语言:
∵ AB//CD (已知)
∴ ∠2=∠3 (两直线平行,内错角相等)
(3)两直线平行,同旁内角互补.
几何语言:
∵ AB//CD (已知)
∴ ∠3+∠4=180° (两直线平行,同旁内角互补)
平行线的性质
新知讲解
同位角相等, 两直线平行
两直线平行, 同位角相等。
平行线的判定
平行线的性质
条件 结论
条件 结论
思考:
1、判定与性质的条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行, 内错角相等。
同旁内角互补, 两直线平行
两直线平行, 同旁内角互补
2、判定是已知 推出 ;
角的相等或互补
两直线平行
性质是已知 ,说明 。
两直线平行
角的相等或互补
新知讲解
例3 如图所示,已知AB//CD,AD//BC. 判断∠1与∠2是否相等,并说明理由.
解:∠1=∠2.理由如下:
已知AB//CD,根据“两直线平行,同旁内角互补”,
得∠1+∠BAD=180°.
同理,由AD//BC,得∠2+∠BAD=180°.
根据“同角的补角相等”,得∠1=∠2.
新知讲解
例4 如图所示,已知∠ABC+∠C=180°,BD平分∠ABC. ∠CBD与∠D 相等吗 请说明理由.
解:∠CBD=∠D.理由如下:
∵ ∠ABC+∠C=180°.
根据“同旁内角互补,两直线平行”,得AB//CD.
再根据“两直线平行,内错角相等”,得∠D=∠ABD.
∵ BD平分∠ABC,
∴∠CBD=∠ABD.
∴∠CBD=∠D.
新知讲解
1.如图,已知AB∥CD,下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
C
课堂练习
2.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
D
4.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为( )
A.10° B.20° C.30° D.40°
B
3.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
A.50° B.45° C.40° D.30°
C
课堂练习
解: ∠A+∠D=180o. 理由:
∵ AB∥DE ( )
∴∠A= ______ ( )
∵AC∥DF ( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( )
5.如图,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
课堂练习
6.如图,AB∥CD,DE⊥AC,垂足为点E,∠A=105°,求∠D的度数.
解:∵AB∥CD,
∴∠A+∠C=180°(两直线平行,同旁内角互补).
∵∠A=105°,
∴∠C=180°-105°=75°.
又∵DE⊥AC,
∴∠DEC=90°,
∴∠C+∠D=90°.
∴∠D=90°-75°=15°.
课堂练习
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
直线的位置关系
角的数量关系
性质
角的数量关系
直线的位置关系
判定
课堂总结
https://www.21cnjy.com/help/help_extract.php
1.4 平行线的性质(2)
浙教版 七年级下册
新知导入
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
应用格式:
∴∠1=∠2
(两直线平行,同位角相等)
∵a ∥ b(已知)
b
1
2
a
c
平行线的性质1:
如图所示,直线AB//CD,并被直线EF 所截.
∠3与∠1有什么关系?∠2与∠3相等吗
解:∠1=∠3(对顶角相等)
∠2=∠3.理由如下:
∵ AB//CD(已知)
∴ ∠1=∠2(两直线平行,同位角相等)
又∵ ∠1=∠3(对顶角相等)
∴ ∠2=∠3(等量代换)
新知讲解
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简单说成,两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等).
∵a∥b(已知),
应用格式:
新知讲解
如图所示,直线AB//CD,并被直线EF 所截.
∠4与∠2有什么关系?∠3与∠4的和是多少度
解:∠2+∠4=180°(平角的意义)
∠3+∠4=180°.理由如下:
∵ AB//CD(已知)
∴ ∠2=∠3(两直线平行,内错角相等)
又∵ ∠2+∠4=180°(平角的意义)
∴ ∠3+∠4=180°.(等量代换)
新知讲解
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简单说成,两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补).
∵a∥b(已知),
应用格式:
新知讲解
如图所示,AB,CD被EF所截,AB//CD,∠1=120°.求∠2,∠3的大小(填空,并说明理由).
解:已知∠1=120°,
根据(__________________________)
则∠2=_______
根据(______________________________),得
∠3=_______-∠1=_______.
两直线平行,内错角相等
120°
两直线平行,同旁内角互补
180°
60°
巩固练习
(1)两直线平行,同位角相等.
几何语言:
∵ AB//CD (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
(2)两直线平行,内错角相等.
几何语言:
∵ AB//CD (已知)
∴ ∠2=∠3 (两直线平行,内错角相等)
(3)两直线平行,同旁内角互补.
几何语言:
∵ AB//CD (已知)
∴ ∠3+∠4=180° (两直线平行,同旁内角互补)
平行线的性质
新知讲解
同位角相等, 两直线平行
两直线平行, 同位角相等。
平行线的判定
平行线的性质
条件 结论
条件 结论
思考:
1、判定与性质的条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行, 内错角相等。
同旁内角互补, 两直线平行
两直线平行, 同旁内角互补
2、判定是已知 推出 ;
角的相等或互补
两直线平行
性质是已知 ,说明 。
两直线平行
角的相等或互补
新知讲解
例3 如图所示,已知AB//CD,AD//BC. 判断∠1与∠2是否相等,并说明理由.
解:∠1=∠2.理由如下:
已知AB//CD,根据“两直线平行,同旁内角互补”,
得∠1+∠BAD=180°.
同理,由AD//BC,得∠2+∠BAD=180°.
根据“同角的补角相等”,得∠1=∠2.
新知讲解
例4 如图所示,已知∠ABC+∠C=180°,BD平分∠ABC. ∠CBD与∠D 相等吗 请说明理由.
解:∠CBD=∠D.理由如下:
∵ ∠ABC+∠C=180°.
根据“同旁内角互补,两直线平行”,得AB//CD.
再根据“两直线平行,内错角相等”,得∠D=∠ABD.
∵ BD平分∠ABC,
∴∠CBD=∠ABD.
∴∠CBD=∠D.
新知讲解
1.如图,已知AB∥CD,下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
C
课堂练习
2.如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
D
4.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B,若∠1=70°,则∠2的度数为( )
A.10° B.20° C.30° D.40°
B
3.如图,直线l1∥l2,CD⊥AB于点D,∠1=50°,则∠BCD的度数为( )
A.50° B.45° C.40° D.30°
C
课堂练习
解: ∠A+∠D=180o. 理由:
∵ AB∥DE ( )
∴∠A= ______ ( )
∵AC∥DF ( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( )
5.如图,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
课堂练习
6.如图,AB∥CD,DE⊥AC,垂足为点E,∠A=105°,求∠D的度数.
解:∵AB∥CD,
∴∠A+∠C=180°(两直线平行,同旁内角互补).
∵∠A=105°,
∴∠C=180°-105°=75°.
又∵DE⊥AC,
∴∠DEC=90°,
∴∠C+∠D=90°.
∴∠D=90°-75°=15°.
课堂练习
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
直线的位置关系
角的数量关系
性质
角的数量关系
直线的位置关系
判定
课堂总结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
