1.3平行线的判定(1) 课件(共22张PPT)
文档属性
| 名称 | 1.3平行线的判定(1) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-15 09:25:40 | ||
图片预览





文档简介
(共22张PPT)
1.3平行线的判定
第1课时
浙教版 七年级下
新知导入
温故知新
(1)在同一平面内,直线a、b的位置关系有几种?
相交
平行
(2)平行线的定义是什么?
在同一平面内,不相交的两条直线叫做平行线
生活中的数学
工人师傅完成斑马线的施工后,想知道是否平行你有什么好办法吗?
小李说:可以根据平行线的定义,把它们向两边无限延长,看看是否有交点.
小邓说:理论上是对的,但是我觉得可操作性不强.
我们要判断两条直线是否平行,除了用平行线的定义,还有其他方法吗?
新知导入
合作探究
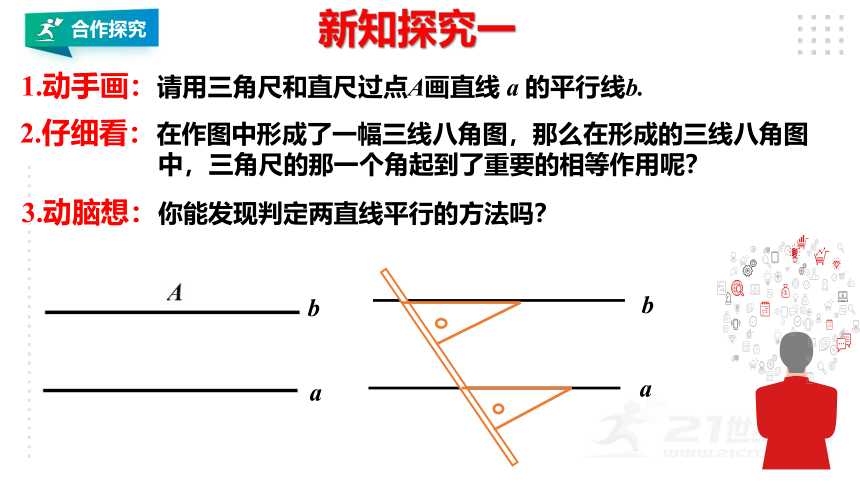
1.动手画:请用三角尺和直尺过点A画直线 a 的平行线b.
2.仔细看:在作图中形成了一幅三线八角图,那么在形成的三线八角图
中,三角尺的那一个角起到了重要的相等作用呢?
3.动脑想:你能发现判定两直线平行的方法吗?
a
b
a
b
新知探究一
一般的,判断两条直线平行有下面的方法:
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.简单的说:同位角相等两直线平行
几何语言:
∵∠1=∠2
∴ a∥b(同位角相等,两直线平行)
新知探究
合作探究
课堂练习
1.如图:直线 a、b被直线c、d 被所截.
(1)若∠1=∠2,则___∥___(根据_________,两直线平行)
(2)若∠___=∠___,则___∥___
a
b
同位角相等
3
2
c
d
填一填
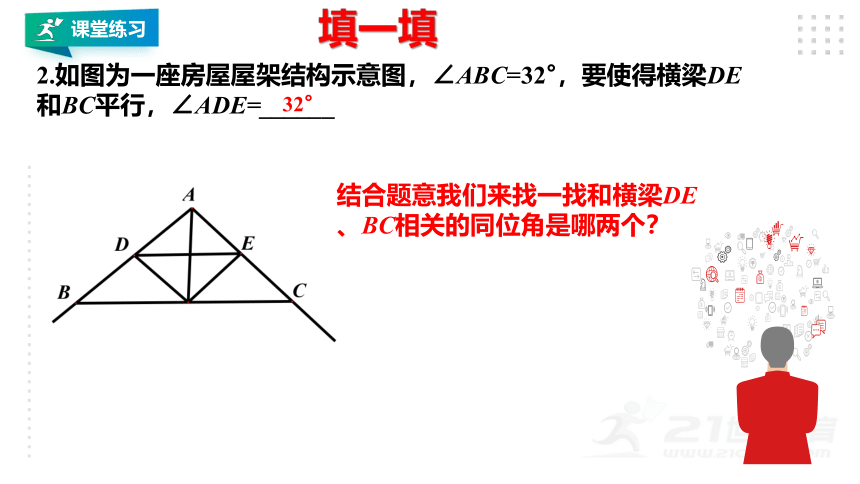
2.如图为一座房屋屋架结构示意图,∠ABC=32°,要使得横梁DE和BC平行,∠ADE=______
课堂练习
32°
填一填
结合题意我们来找一找和横梁DE、BC相关的同位角是哪两个?
课堂练习
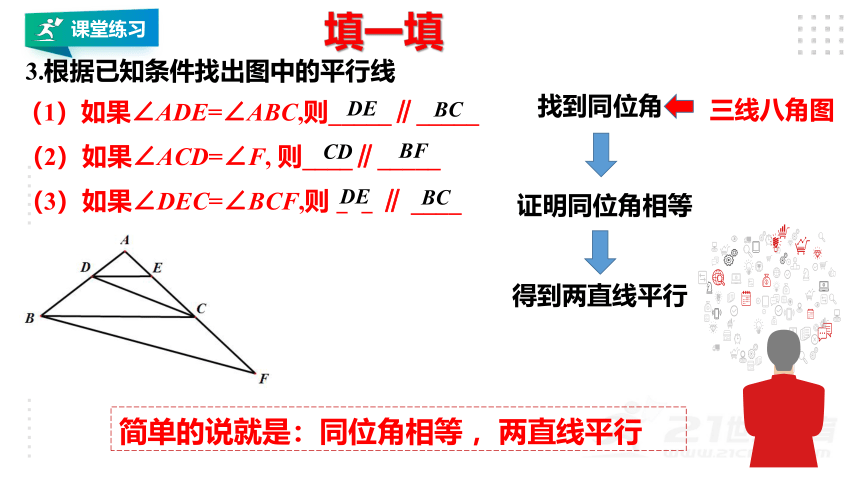
3.根据已知条件找出图中的平行线
填一填
(1)如果∠ADE=∠ABC,则_____∥_____
(2)如果∠ACD=∠F, 则____∥_____
(3)如果∠DEC=∠BCF,则__∥ ____
DE
BC
CD
BF
DE
BC
找到同位角
证明同位角相等
得到两直线平行
三线八角图
简单的说就是:同位角相等 ,两直线平行
例题分析
例题讲解
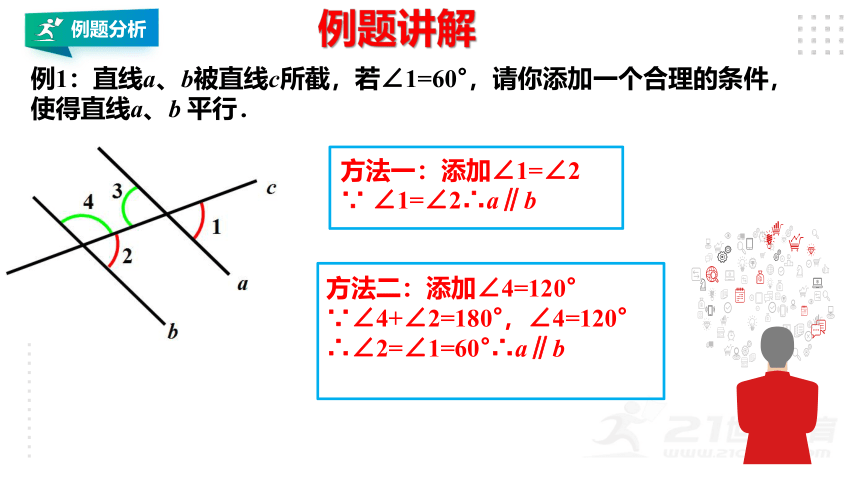
方法一:添加∠1=∠2
∵ ∠1=∠2∴a∥b
方法二:添加∠4=120°
∵∠4+∠2=180°,∠4=120°
∴∠2=∠1=60°∴a∥b
例1:直线a、b被直线c所截,若∠1=60°,请你添加一个合理的条件,使得直线a、b 平行.
合作探究
探究新知二
3
∵∠1=∠3,∴∠2+∠3=90°
∴AB⊥a
∵∠1+∠2=90°,∠1+∠EFD=90°
∴∠2=∠EFD,∴AB∥CD(同位角相等,两直线平行)
如图,已知直线AB,CD被直线a所截,直线CD⊥直线a,若∠1和∠2互余,请你判断AB、a的位置关系, AB和CD的位置关系并说明理由.
探究新知二
3
∵∠1=∠3,∴∠2+∠3=90°
∴AB⊥a
如图,已知直线AB,CD被直线a所截,直线CD⊥直线a,若∠1和∠2互余,请你判断AB、a的位置关系, AB和CD的位置关系并说明理由.
∵ AB⊥a ,CD⊥a
∴AB∥CD
∴∠4=∠5
合作探究
一般到特殊
推论:
在同一平面内,垂直于同一条直线的两条直线互相平行
探究新知二
合作探究
拓展应用
实际应用:同学们还记得课前的问题吗?工人师傅在路口画上了斑马线,他们想检验斑马线是否平行,你能帮助他们吗?请你设计一个方案来检验斑马线是否平行.
方案一:斜方向构造一条截线,使他们构成同位角,然后再检验这些同位角是否相等.
方案二:垂直方向构造一条截线,然后检验各同位角是否是直角.
发散新知
向左转15°
练习巩固
练习1:某人骑自行车从A地出发,沿着正东方向前进至点B处后,右转15°,沿着直线向前行驶到C处(如图);若他仍想按正东方向行驶,请画出他应该怎么样调整行驶的路线?说明理由.
拓展应用
课堂练习
练习巩固
∵BF平分∠ABC,∴∠ABF=∠CBF
又∵∠CBF=∠CFB=∠EFD,∴ ∠EFD=∠ABF
练习2:已知BF平分∠ABC并且交AD的延长线于点E,∠CBF=∠CFB.
求证CD∥AB.
∴CD∥AB(同位角相等,两直线平行)
小李的解答如下:
∵ ∠1=∠2,
∴ AB∥CD(同位角相等两直线平行)
请你再添加一个条件,使得AB∥CD,并说明理由.
发散新知:
如图,点B、D在直线GH上,已知∠1=∠2,请你判断AB、CD是否平行,并说明理由.
(1)∠EBH=∠FDH
(2)AB、CD分别是∠EBH、∠FDH的角平分线
课堂练习
发散新知
如图在四边形ABCD中,∠A=∠B,∠D=∠C,证明AB∥CD.
∵∠D=∠C,∴∠EDC=∠ECD
又∵ ∠EDC+∠ECD+∠E=∠ E+∠A+∠B
∴2 ∠EDC =2∠A, ∴∠EDC =∠A
∴ AB∥CD
课堂练习
发散新知
课堂练习
课堂总结
两直线平行线的判定方法
平行线定义
证明同位角相等
找同位角
推论
常见的等角
构造同位角
课堂总结
完成作业本①1.3平行线的判定(1)
作业布置
https://www.21cnjy.com/help/help_extract.php
1.3平行线的判定
第1课时
浙教版 七年级下
新知导入
温故知新
(1)在同一平面内,直线a、b的位置关系有几种?
相交
平行
(2)平行线的定义是什么?
在同一平面内,不相交的两条直线叫做平行线
生活中的数学
工人师傅完成斑马线的施工后,想知道是否平行你有什么好办法吗?
小李说:可以根据平行线的定义,把它们向两边无限延长,看看是否有交点.
小邓说:理论上是对的,但是我觉得可操作性不强.
我们要判断两条直线是否平行,除了用平行线的定义,还有其他方法吗?
新知导入
合作探究
1.动手画:请用三角尺和直尺过点A画直线 a 的平行线b.
2.仔细看:在作图中形成了一幅三线八角图,那么在形成的三线八角图
中,三角尺的那一个角起到了重要的相等作用呢?
3.动脑想:你能发现判定两直线平行的方法吗?
a
b
a
b
新知探究一
一般的,判断两条直线平行有下面的方法:
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.简单的说:同位角相等两直线平行
几何语言:
∵∠1=∠2
∴ a∥b(同位角相等,两直线平行)
新知探究
合作探究
课堂练习
1.如图:直线 a、b被直线c、d 被所截.
(1)若∠1=∠2,则___∥___(根据_________,两直线平行)
(2)若∠___=∠___,则___∥___
a
b
同位角相等
3
2
c
d
填一填
2.如图为一座房屋屋架结构示意图,∠ABC=32°,要使得横梁DE和BC平行,∠ADE=______
课堂练习
32°
填一填
结合题意我们来找一找和横梁DE、BC相关的同位角是哪两个?
课堂练习
3.根据已知条件找出图中的平行线
填一填
(1)如果∠ADE=∠ABC,则_____∥_____
(2)如果∠ACD=∠F, 则____∥_____
(3)如果∠DEC=∠BCF,则__∥ ____
DE
BC
CD
BF
DE
BC
找到同位角
证明同位角相等
得到两直线平行
三线八角图
简单的说就是:同位角相等 ,两直线平行
例题分析
例题讲解
方法一:添加∠1=∠2
∵ ∠1=∠2∴a∥b
方法二:添加∠4=120°
∵∠4+∠2=180°,∠4=120°
∴∠2=∠1=60°∴a∥b
例1:直线a、b被直线c所截,若∠1=60°,请你添加一个合理的条件,使得直线a、b 平行.
合作探究
探究新知二
3
∵∠1=∠3,∴∠2+∠3=90°
∴AB⊥a
∵∠1+∠2=90°,∠1+∠EFD=90°
∴∠2=∠EFD,∴AB∥CD(同位角相等,两直线平行)
如图,已知直线AB,CD被直线a所截,直线CD⊥直线a,若∠1和∠2互余,请你判断AB、a的位置关系, AB和CD的位置关系并说明理由.
探究新知二
3
∵∠1=∠3,∴∠2+∠3=90°
∴AB⊥a
如图,已知直线AB,CD被直线a所截,直线CD⊥直线a,若∠1和∠2互余,请你判断AB、a的位置关系, AB和CD的位置关系并说明理由.
∵ AB⊥a ,CD⊥a
∴AB∥CD
∴∠4=∠5
合作探究
一般到特殊
推论:
在同一平面内,垂直于同一条直线的两条直线互相平行
探究新知二
合作探究
拓展应用
实际应用:同学们还记得课前的问题吗?工人师傅在路口画上了斑马线,他们想检验斑马线是否平行,你能帮助他们吗?请你设计一个方案来检验斑马线是否平行.
方案一:斜方向构造一条截线,使他们构成同位角,然后再检验这些同位角是否相等.
方案二:垂直方向构造一条截线,然后检验各同位角是否是直角.
发散新知
向左转15°
练习巩固
练习1:某人骑自行车从A地出发,沿着正东方向前进至点B处后,右转15°,沿着直线向前行驶到C处(如图);若他仍想按正东方向行驶,请画出他应该怎么样调整行驶的路线?说明理由.
拓展应用
课堂练习
练习巩固
∵BF平分∠ABC,∴∠ABF=∠CBF
又∵∠CBF=∠CFB=∠EFD,∴ ∠EFD=∠ABF
练习2:已知BF平分∠ABC并且交AD的延长线于点E,∠CBF=∠CFB.
求证CD∥AB.
∴CD∥AB(同位角相等,两直线平行)
小李的解答如下:
∵ ∠1=∠2,
∴ AB∥CD(同位角相等两直线平行)
请你再添加一个条件,使得AB∥CD,并说明理由.
发散新知:
如图,点B、D在直线GH上,已知∠1=∠2,请你判断AB、CD是否平行,并说明理由.
(1)∠EBH=∠FDH
(2)AB、CD分别是∠EBH、∠FDH的角平分线
课堂练习
发散新知
如图在四边形ABCD中,∠A=∠B,∠D=∠C,证明AB∥CD.
∵∠D=∠C,∴∠EDC=∠ECD
又∵ ∠EDC+∠ECD+∠E=∠ E+∠A+∠B
∴2 ∠EDC =2∠A, ∴∠EDC =∠A
∴ AB∥CD
课堂练习
发散新知
课堂练习
课堂总结
两直线平行线的判定方法
平行线定义
证明同位角相等
找同位角
推论
常见的等角
构造同位角
课堂总结
完成作业本①1.3平行线的判定(1)
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
