1.3平行线的判定(2) 课件(共17张PPT)
文档属性
| 名称 | 1.3平行线的判定(2) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
1.3平行线的判定(2)
第2课时
浙教版 七年级下
新知探究
探究1:如图所示,直线AB,CD 被直线EF 所截.
若∠2=∠3,则AB 与CD 平行吗
解:
平行,理由如下:
又∵∠2=∠3
∵∠1=∠3
∴∠1=∠2
∴AB∥CD
(同位角相等,两直线平行)
由此,可获得平行线的判定方法:
符号语言:
∵∠2=∠3
∴AB∥CD
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
2
3
E
F
A
B
C
D
1
4
分析:已经有的方法:“同位角相等,两直线平行”
(对顶角相等)
课堂练习
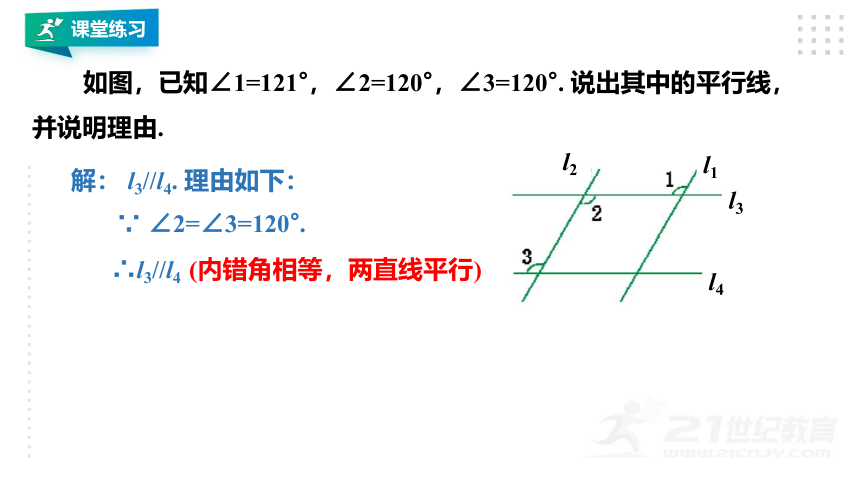
如图,已知∠1=121°,∠2=120°,∠3=120°. 说出其中的平行线, 并说明理由.
解: l3//l4. 理由如下:
∵ ∠2=∠3=120°.
∴l3//l4 (内错角相等,两直线平行)
l4
l1
l3
l2
课堂练习
A
B
D
C
E
3
2
1
2. 如图,∠1=∠2=∠3. 填空:
(1)已知∠1=∠2,根据( ),
(2)已知∠2=∠3,根据( ),
可得 ∥ .
可得 ∥ .
同位角相等,两直线平行
内错角相等,两直线平行
AD
BC
AB
CD
探究2:如图所示,直线AB,CD 被直线EF 所截.
若∠3+∠4=180°,则AB 与CD 平行吗
解:
平行,理由如下:
∵ ∠2+∠4=180 °
∠3+∠4=180 °
∴ ∠2=∠3
∴ AB //CD
(同角的补角相等)
还能怎么证?
(内错角相等,两直线平行)
由此,又获得平行线的判定方法:
符号语言:
∵∠3+∠4=180 °
∴AB∥CD
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
2
3
E
F
A
B
C
D
1
4
新知探究
课堂练习
A
B
1
2
3
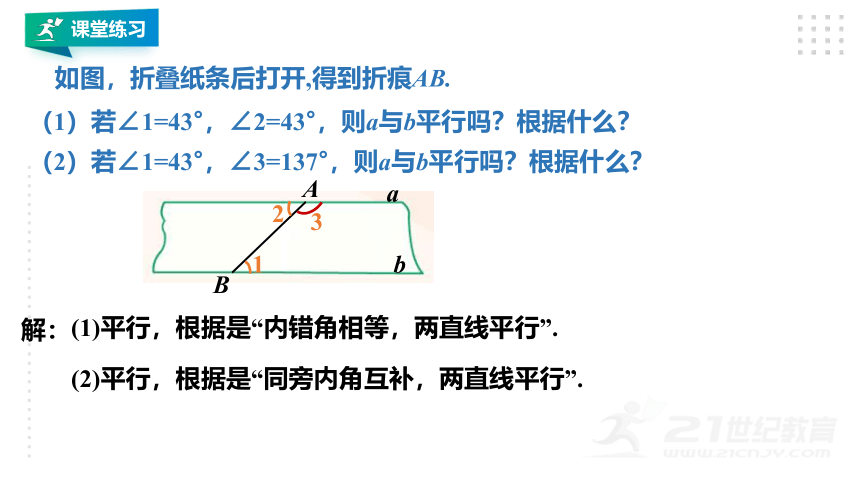
如图,折叠纸条后打开,得到折痕AB.
(1)若∠1=43°,∠2=43°,则a与b平行吗?根据什么?
(2)若∠1=43°,∠3=137°,则a与b平行吗?根据什么?
a
b
解:
(1)平行,根据是“内错角相等,两直线平行”.
(2)平行,根据是“同旁内角互补,两直线平行”.
归纳小结
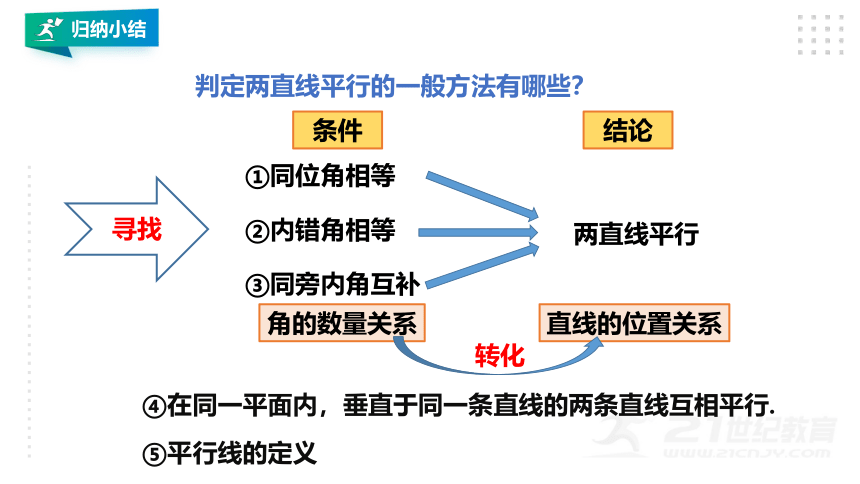
条件
结论
①同位角相等
②内错角相等
③同旁内角互补
两直线平行
角的数量关系
直线的位置关系
转化
判定两直线平行的一般方法有哪些?
⑤平行线的定义
④在同一平面内,垂直于同一条直线的两条直线互相平行.
寻找
例题分析
例3:如图所示,AC⊥CD 于点C,∠1与∠2互余. 判断AB,CD 是否
平行,并说明理由.
解:AB//CD. 理由如下:
∵AC⊥CD
∴∠2+∠3=90°
又∵∠1+∠2=90°
∴∠1=∠3
∴AB//CD
(内错角相等,两直线平行)
(同角的余角相等)
3
A
B
1
2
D
C
寻找关系角
思考:你有几种不同的证法?
说明相等
例题分析
例4. 如图,AP平分∠BAC,CP平分∠ACD,∠1+∠2=90°,
判断AB,CD是否平行,说明理由.
A
B
D
C
P
2
1
解: AB//CD.理由如下:
∵AP平分∠BAC
∴∠BAC=2∠1
∵CP平分∠ACD
∴∠ACD=2∠2
∵∠1+∠2=90°
∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°
∴AB//CD
(同旁内角互补,两直线平行)
寻找关系角
整体思想
说明互补
l
a
b
1
2
1. 如图,直线a,b被直线l所截. 若∠1=62°,∠2=118°,
则a与b平行吗?请说明理由.
解:a//b. 理由如下:
∵ ∠2=∠3=118°,
∴∠1+∠3=180°
∠1=62°
∴a//b (同旁内角互补,两直线平行)
3
比一比:你有几种不同的证法?
解法一:
解法二:
4
5
∵ ∠4=180°-∠2=180°-118°=62°,
∠1=62°
∴∠1=∠4
∴a//b (内错角相等,两直线平行)
解法三:
∵ ∠5=180°-∠2=180°-118°=62°,
∠1=62°
∴∠1=∠5
∴a//b (同位角相等,两直线平行)
课堂练习
2.如图所示,给出下列条件:
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5;
⑤∠B=∠D.
其中,一定能判定AB//CD的条件的个数有( )
A.5个 B.4个 C.3个 D.2个
C
对应关系要正确
课堂练习
2
3
3.如图沿AB折叠,两种测量结果中一定能判定纸带的两条边线AC、BD
互相平行的是( )
A. 如图①所示,测得∠1=∠2
B. 如图②所示,测得∠2=∠3
1
2
B
图①
图②
A
B
A
B
C
D
D
C
寻找关系角
折叠→打开
课堂练习
2.台球运动中,如果母球P击中桌边点A,经桌边反弹后击中相邻的另一条桌边点B,再次反弹,那么母球P经过的路线BC与PA平行吗?请说明你判断的理由.(根据反射原理,可知∠1=∠2,∠3=∠4.)
P
A
B
C
1
2
3
4
解:PA∥BC,理由如下:
∵∠1=∠2,∠3=∠4
又∵∠2+∠3=90°
∴∠1+∠2+∠3+∠4=180°
∴∠PAB+∠ABC=360°-180°=180°
∴PA∥BC
∵∠PAB+∠1+∠2=180°,
∠ABC+∠3+∠4=180°
(同旁内角互补,两直线平行)
D
寻找关系角
说明互补
说理过程的表达
同旁内角:
∠CBA与∠PAB
课堂练习
课堂总结
平行线的判定方法
直观
说理
①同位角相等,两直线平行.
②内错角相等,两直线平行.
③同旁内角互补,两直线平行.
④同一平面内,垂直于同一直线的两条
直线互相平行.
⑤平行线的定义.
寻找关系角(或构造)
说明相等(或互补)
说理过程的表达
流程
证得平行
(注意对应)
作业布置
完成作业本(2)1.3平行线的判定(2)
https://www.21cnjy.com/help/help_extract.php
1.3平行线的判定(2)
第2课时
浙教版 七年级下
新知探究
探究1:如图所示,直线AB,CD 被直线EF 所截.
若∠2=∠3,则AB 与CD 平行吗
解:
平行,理由如下:
又∵∠2=∠3
∵∠1=∠3
∴∠1=∠2
∴AB∥CD
(同位角相等,两直线平行)
由此,可获得平行线的判定方法:
符号语言:
∵∠2=∠3
∴AB∥CD
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
2
3
E
F
A
B
C
D
1
4
分析:已经有的方法:“同位角相等,两直线平行”
(对顶角相等)
课堂练习
如图,已知∠1=121°,∠2=120°,∠3=120°. 说出其中的平行线, 并说明理由.
解: l3//l4. 理由如下:
∵ ∠2=∠3=120°.
∴l3//l4 (内错角相等,两直线平行)
l4
l1
l3
l2
课堂练习
A
B
D
C
E
3
2
1
2. 如图,∠1=∠2=∠3. 填空:
(1)已知∠1=∠2,根据( ),
(2)已知∠2=∠3,根据( ),
可得 ∥ .
可得 ∥ .
同位角相等,两直线平行
内错角相等,两直线平行
AD
BC
AB
CD
探究2:如图所示,直线AB,CD 被直线EF 所截.
若∠3+∠4=180°,则AB 与CD 平行吗
解:
平行,理由如下:
∵ ∠2+∠4=180 °
∠3+∠4=180 °
∴ ∠2=∠3
∴ AB //CD
(同角的补角相等)
还能怎么证?
(内错角相等,两直线平行)
由此,又获得平行线的判定方法:
符号语言:
∵∠3+∠4=180 °
∴AB∥CD
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
2
3
E
F
A
B
C
D
1
4
新知探究
课堂练习
A
B
1
2
3
如图,折叠纸条后打开,得到折痕AB.
(1)若∠1=43°,∠2=43°,则a与b平行吗?根据什么?
(2)若∠1=43°,∠3=137°,则a与b平行吗?根据什么?
a
b
解:
(1)平行,根据是“内错角相等,两直线平行”.
(2)平行,根据是“同旁内角互补,两直线平行”.
归纳小结
条件
结论
①同位角相等
②内错角相等
③同旁内角互补
两直线平行
角的数量关系
直线的位置关系
转化
判定两直线平行的一般方法有哪些?
⑤平行线的定义
④在同一平面内,垂直于同一条直线的两条直线互相平行.
寻找
例题分析
例3:如图所示,AC⊥CD 于点C,∠1与∠2互余. 判断AB,CD 是否
平行,并说明理由.
解:AB//CD. 理由如下:
∵AC⊥CD
∴∠2+∠3=90°
又∵∠1+∠2=90°
∴∠1=∠3
∴AB//CD
(内错角相等,两直线平行)
(同角的余角相等)
3
A
B
1
2
D
C
寻找关系角
思考:你有几种不同的证法?
说明相等
例题分析
例4. 如图,AP平分∠BAC,CP平分∠ACD,∠1+∠2=90°,
判断AB,CD是否平行,说明理由.
A
B
D
C
P
2
1
解: AB//CD.理由如下:
∵AP平分∠BAC
∴∠BAC=2∠1
∵CP平分∠ACD
∴∠ACD=2∠2
∵∠1+∠2=90°
∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°
∴AB//CD
(同旁内角互补,两直线平行)
寻找关系角
整体思想
说明互补
l
a
b
1
2
1. 如图,直线a,b被直线l所截. 若∠1=62°,∠2=118°,
则a与b平行吗?请说明理由.
解:a//b. 理由如下:
∵ ∠2=∠3=118°,
∴∠1+∠3=180°
∠1=62°
∴a//b (同旁内角互补,两直线平行)
3
比一比:你有几种不同的证法?
解法一:
解法二:
4
5
∵ ∠4=180°-∠2=180°-118°=62°,
∠1=62°
∴∠1=∠4
∴a//b (内错角相等,两直线平行)
解法三:
∵ ∠5=180°-∠2=180°-118°=62°,
∠1=62°
∴∠1=∠5
∴a//b (同位角相等,两直线平行)
课堂练习
2.如图所示,给出下列条件:
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5;
⑤∠B=∠D.
其中,一定能判定AB//CD的条件的个数有( )
A.5个 B.4个 C.3个 D.2个
C
对应关系要正确
课堂练习
2
3
3.如图沿AB折叠,两种测量结果中一定能判定纸带的两条边线AC、BD
互相平行的是( )
A. 如图①所示,测得∠1=∠2
B. 如图②所示,测得∠2=∠3
1
2
B
图①
图②
A
B
A
B
C
D
D
C
寻找关系角
折叠→打开
课堂练习
2.台球运动中,如果母球P击中桌边点A,经桌边反弹后击中相邻的另一条桌边点B,再次反弹,那么母球P经过的路线BC与PA平行吗?请说明你判断的理由.(根据反射原理,可知∠1=∠2,∠3=∠4.)
P
A
B
C
1
2
3
4
解:PA∥BC,理由如下:
∵∠1=∠2,∠3=∠4
又∵∠2+∠3=90°
∴∠1+∠2+∠3+∠4=180°
∴∠PAB+∠ABC=360°-180°=180°
∴PA∥BC
∵∠PAB+∠1+∠2=180°,
∠ABC+∠3+∠4=180°
(同旁内角互补,两直线平行)
D
寻找关系角
说明互补
说理过程的表达
同旁内角:
∠CBA与∠PAB
课堂练习
课堂总结
平行线的判定方法
直观
说理
①同位角相等,两直线平行.
②内错角相等,两直线平行.
③同旁内角互补,两直线平行.
④同一平面内,垂直于同一直线的两条
直线互相平行.
⑤平行线的定义.
寻找关系角(或构造)
说明相等(或互补)
说理过程的表达
流程
证得平行
(注意对应)
作业布置
完成作业本(2)1.3平行线的判定(2)
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
