1.4 平行线的性质(二)(第2课时) 同步练习(含解析)
文档属性
| 名称 | 1.4 平行线的性质(二)(第2课时) 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 10:23:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.4 第2课时 平行线的性质(二)
知识点 1 两直线平行,内错角相等
1.如图1-4-16所示,AB∥CD,直线l分别与AB,CD相交.若∠1=50°,则∠2的度数为 .
图1-4-16
2.如图1-4-17,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,那么第二次的拐角∠B是 °,依据是 .
图1-4-17
3.已知直线m∥n,将一块含30°角的三角尺ABC按图1-4-18所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=20°,则∠2的度数为 ( )
A.40° B.45° C.50° D.60°
图1-4-18
4.如图1-4-19,AB∥CD,∠B=35°,∠DCE=75°,则∠ACB的度数为( )
图1-4-19
A.50° B.60° C.70° D.80°
知识点 2 两直线平行,同旁内角互补
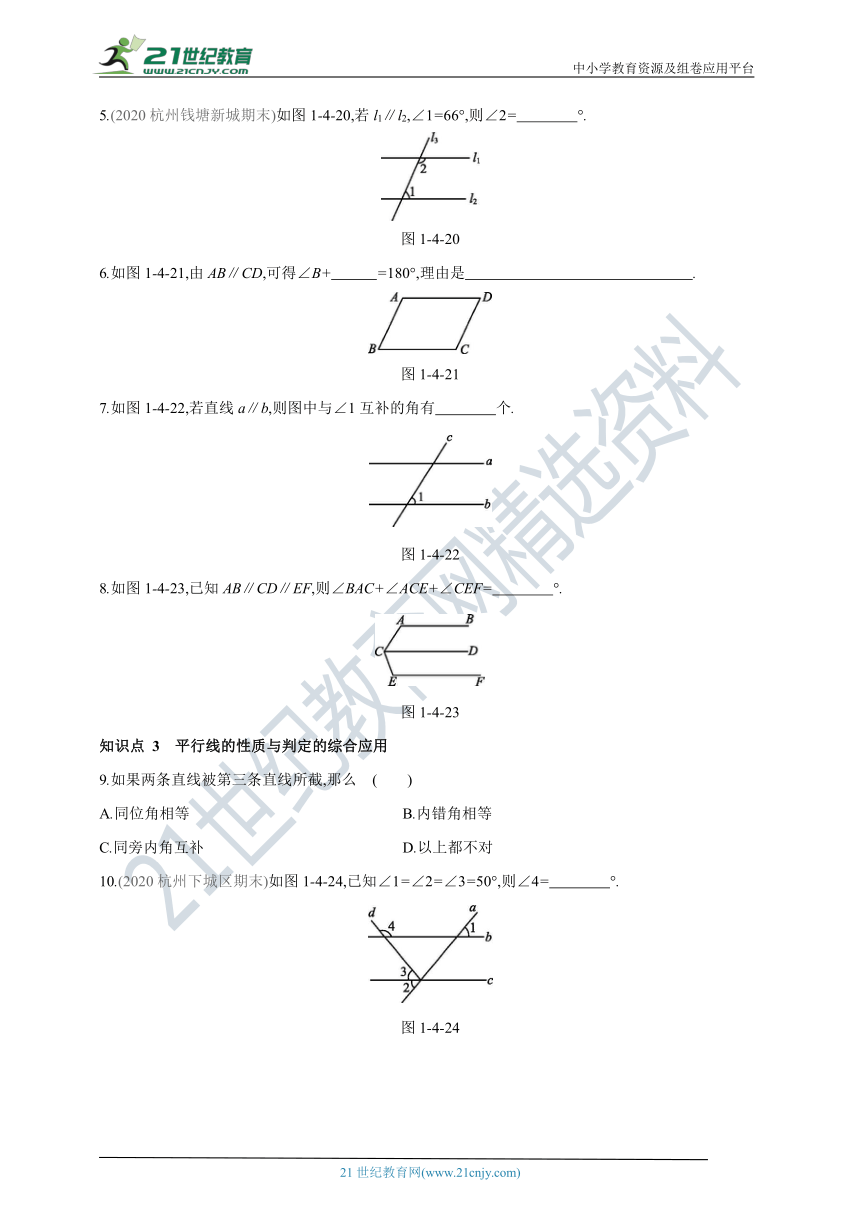
5.(2020杭州钱塘新城期末)如图1-4-20,若l1∥l2,∠1=66°,则∠2= °.
图1-4-20
6.如图1-4-21,由AB∥CD,可得∠B+ =180°,理由是 .
图1-4-21
7.如图1-4-22,若直线a∥b,则图中与∠1互补的角有 个.
图1-4-22
8.如图1-4-23,已知AB∥CD∥EF,则∠BAC+∠ACE+∠CEF= °.
图1-4-23
知识点 3 平行线的性质与判定的综合应用
9.如果两条直线被第三条直线所截,那么 ( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.以上都不对
10.(2020杭州下城区期末)如图1-4-24,已知∠1=∠2=∠3=50°,则∠4= °.
图1-4-24
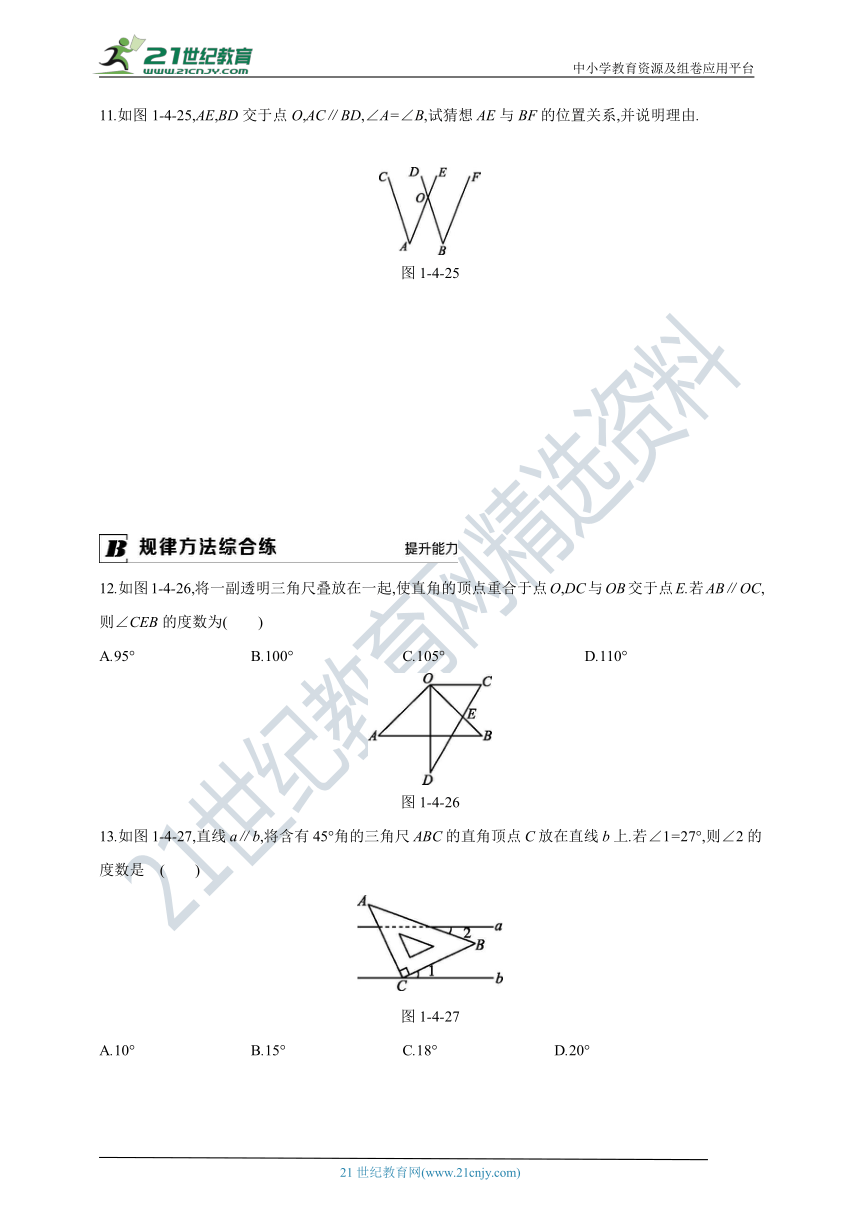
11.如图1-4-25,AE,BD交于点O,AC∥BD,∠A=∠B,试猜想AE与BF的位置关系,并说明理由.
图1-4-25
12.如图1-4-26,将一副透明三角尺叠放在一起,使直角的顶点重合于点O,DC与OB交于点E.若AB∥OC,则∠CEB的度数为( )
A.95° B.100° C.105° D.110°
图1-4-26
13.如图1-4-27,直线a∥b,将含有45°角的三角尺ABC的直角顶点C放在直线b上.若∠1=27°,则∠2的度数是 ( )
图1-4-27
A.10° B.15° C.18° D.20°
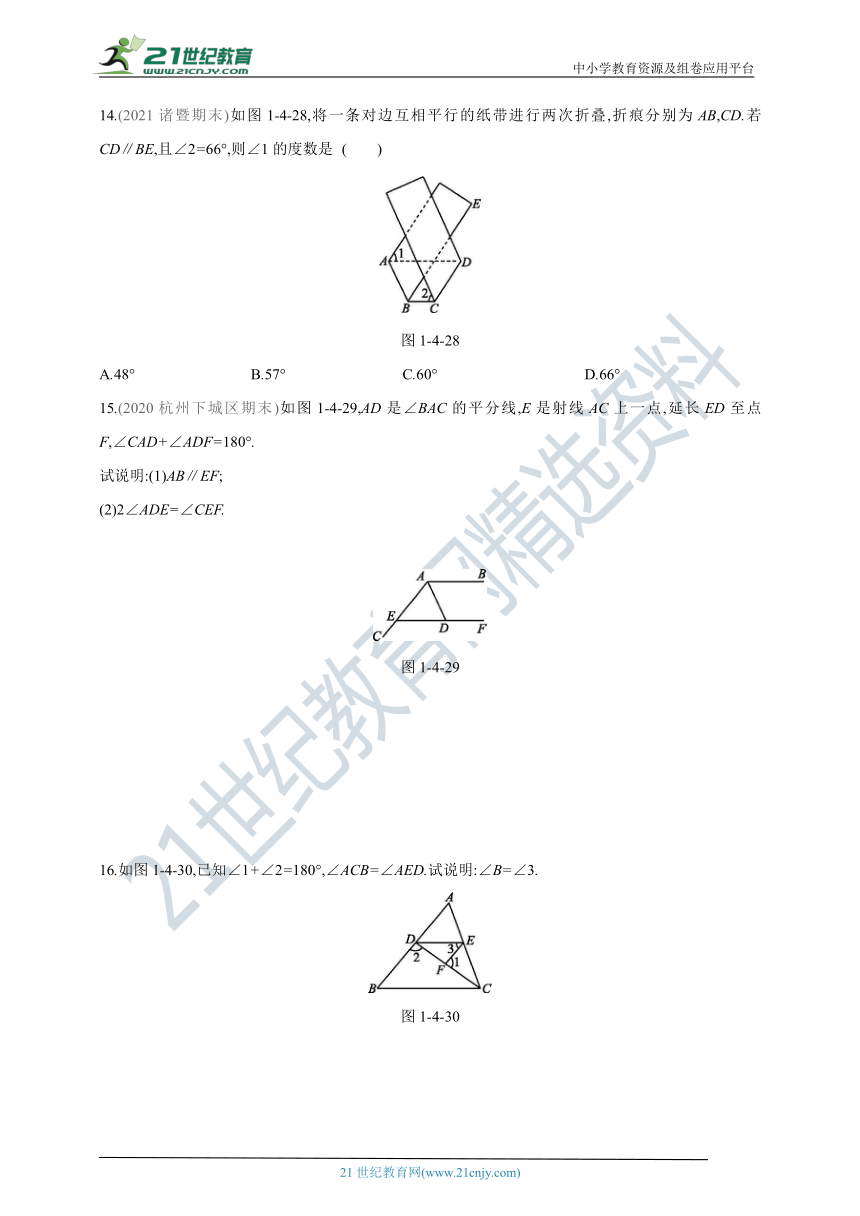
14.(2021诸暨期末)如图1-4-28,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,且∠2=66°,则∠1的度数是 ( )
图1-4-28
A.48° B.57° C.60° D.66°
15.(2020杭州下城区期末)如图1-4-29,AD是∠BAC的平分线,E是射线AC上一点,延长ED至点F,∠CAD+∠ADF=180°.
试说明:(1)AB∥EF;
(2)2∠ADE=∠CEF.
图1-4-29
16.如图1-4-30,已知∠1+∠2=180°,∠ACB=∠AED.试说明:∠B=∠3.
图1-4-30
17.如图1-4-31,一条铁路修到一个村庄附近时,需拐弯绕道而过,如果第一次拐的角∠A是105°,第二次拐的角∠B是135°,第三次拐的角是∠C,这时的铁路恰好和第一次拐弯之前的铁路平行,那么∠C应为多少度
图1-4-31
详解详析
1.50° [解析] 两直线平行,内错角相等.
2.135 两直线平行,内错角相等
3.C
4.C [解析] ∵AB∥CD,∠B=35°,
∴∠BCD=35°.
又∵∠DCE=75°,
∴∠ACB=180°-75°-35°=70°.
故选C.
5.114
6.∠C 两直线平行,同旁内角互补
7.4
8.360 [解析] ∵AB∥CD,
∴∠BAC+∠ACD=180°.①
∵CD∥EF,∴∠DCE+∠CEF=180°.②
①+②,得∠BAC+∠ACD+∠DCE+∠CEF=180°+180°=360°,
即∠BAC+∠ACE+∠CEF=360°.
9.D
10.130 [解析] 如图.∵∠1=∠2,∠1=∠5,
∴∠5=∠2,
∴b∥c,∴∠3+∠6=180°.
∵∠3=50°,∴∠6=130°,
∴∠4=∠6=130°.
故答案为130.
11.解:AE∥BF.
理由:∵AC∥BD,∴∠A=∠DOE.
又∵∠A=∠B,∴∠DOE=∠B,
∴AE∥BF.
12.C
13.C [解析] 如图,过点B作BE∥直线a.
∵直线a∥b,∴a∥BE∥b,
∴∠2=∠ABE,∠CBE=∠1=27°.
又∵∠ABC=45°,
∴∠2=∠ABE=45°-27°=18°.
故选C.
14.B [解析] 如图,延长BC到点F.
∵纸带对边互相平行,
∴∠4=∠3=∠1.
由折叠可得,∠DCF=∠5.
∵CD∥BE,
∴∠DCF=∠4,
∴∠5=∠4.
∵∠2+∠5+∠DCF=180°,
∴66°+2∠4=180°,即∠4=57°,
∴∠1=57°.
故选B.
15.解:(1)∵AD是∠BAC的平分线,
∴∠CAD=∠DAB.
又∵∠CAD+∠ADF=180°,
∴∠DAB+∠ADF=180°,
∴AB∥EF.
(2)∵AB∥EF,
∴∠ADE=∠DAB,∠CEF=∠BAC.
∵AD是∠BAC的平分线,
∴2∠DAB=∠BAC,
∴2∠ADE=∠CEF.
16.解:∵∠1+∠DFE=180°,∠1+∠2=180°,
∴∠DFE=∠2,
∴AB∥EF,
∴∠3=∠ADE.
∵∠ACB=∠AED,
∴DE∥BC,
∴∠B=∠ADE,
∴∠B=∠3.
17.解:如图,过点B作射线BE∥CD.
∵CD∥AF,
∴BE∥CD∥AF,
∴∠ABE=∠A=105°,
∴∠CBE=∠ABC-∠ABE=30°.
∵BE∥CD,
∴∠CBE+∠C=180°,
∴∠C=150°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
1.4 第2课时 平行线的性质(二)
知识点 1 两直线平行,内错角相等
1.如图1-4-16所示,AB∥CD,直线l分别与AB,CD相交.若∠1=50°,则∠2的度数为 .
图1-4-16
2.如图1-4-17,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,那么第二次的拐角∠B是 °,依据是 .
图1-4-17
3.已知直线m∥n,将一块含30°角的三角尺ABC按图1-4-18所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=20°,则∠2的度数为 ( )
A.40° B.45° C.50° D.60°
图1-4-18
4.如图1-4-19,AB∥CD,∠B=35°,∠DCE=75°,则∠ACB的度数为( )
图1-4-19
A.50° B.60° C.70° D.80°
知识点 2 两直线平行,同旁内角互补
5.(2020杭州钱塘新城期末)如图1-4-20,若l1∥l2,∠1=66°,则∠2= °.
图1-4-20
6.如图1-4-21,由AB∥CD,可得∠B+ =180°,理由是 .
图1-4-21
7.如图1-4-22,若直线a∥b,则图中与∠1互补的角有 个.
图1-4-22
8.如图1-4-23,已知AB∥CD∥EF,则∠BAC+∠ACE+∠CEF= °.
图1-4-23
知识点 3 平行线的性质与判定的综合应用
9.如果两条直线被第三条直线所截,那么 ( )
A.同位角相等 B.内错角相等
C.同旁内角互补 D.以上都不对
10.(2020杭州下城区期末)如图1-4-24,已知∠1=∠2=∠3=50°,则∠4= °.
图1-4-24
11.如图1-4-25,AE,BD交于点O,AC∥BD,∠A=∠B,试猜想AE与BF的位置关系,并说明理由.
图1-4-25
12.如图1-4-26,将一副透明三角尺叠放在一起,使直角的顶点重合于点O,DC与OB交于点E.若AB∥OC,则∠CEB的度数为( )
A.95° B.100° C.105° D.110°
图1-4-26
13.如图1-4-27,直线a∥b,将含有45°角的三角尺ABC的直角顶点C放在直线b上.若∠1=27°,则∠2的度数是 ( )
图1-4-27
A.10° B.15° C.18° D.20°
14.(2021诸暨期末)如图1-4-28,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,且∠2=66°,则∠1的度数是 ( )
图1-4-28
A.48° B.57° C.60° D.66°
15.(2020杭州下城区期末)如图1-4-29,AD是∠BAC的平分线,E是射线AC上一点,延长ED至点F,∠CAD+∠ADF=180°.
试说明:(1)AB∥EF;
(2)2∠ADE=∠CEF.
图1-4-29
16.如图1-4-30,已知∠1+∠2=180°,∠ACB=∠AED.试说明:∠B=∠3.
图1-4-30
17.如图1-4-31,一条铁路修到一个村庄附近时,需拐弯绕道而过,如果第一次拐的角∠A是105°,第二次拐的角∠B是135°,第三次拐的角是∠C,这时的铁路恰好和第一次拐弯之前的铁路平行,那么∠C应为多少度
图1-4-31
详解详析
1.50° [解析] 两直线平行,内错角相等.
2.135 两直线平行,内错角相等
3.C
4.C [解析] ∵AB∥CD,∠B=35°,
∴∠BCD=35°.
又∵∠DCE=75°,
∴∠ACB=180°-75°-35°=70°.
故选C.
5.114
6.∠C 两直线平行,同旁内角互补
7.4
8.360 [解析] ∵AB∥CD,
∴∠BAC+∠ACD=180°.①
∵CD∥EF,∴∠DCE+∠CEF=180°.②
①+②,得∠BAC+∠ACD+∠DCE+∠CEF=180°+180°=360°,
即∠BAC+∠ACE+∠CEF=360°.
9.D
10.130 [解析] 如图.∵∠1=∠2,∠1=∠5,
∴∠5=∠2,
∴b∥c,∴∠3+∠6=180°.
∵∠3=50°,∴∠6=130°,
∴∠4=∠6=130°.
故答案为130.
11.解:AE∥BF.
理由:∵AC∥BD,∴∠A=∠DOE.
又∵∠A=∠B,∴∠DOE=∠B,
∴AE∥BF.
12.C
13.C [解析] 如图,过点B作BE∥直线a.
∵直线a∥b,∴a∥BE∥b,
∴∠2=∠ABE,∠CBE=∠1=27°.
又∵∠ABC=45°,
∴∠2=∠ABE=45°-27°=18°.
故选C.
14.B [解析] 如图,延长BC到点F.
∵纸带对边互相平行,
∴∠4=∠3=∠1.
由折叠可得,∠DCF=∠5.
∵CD∥BE,
∴∠DCF=∠4,
∴∠5=∠4.
∵∠2+∠5+∠DCF=180°,
∴66°+2∠4=180°,即∠4=57°,
∴∠1=57°.
故选B.
15.解:(1)∵AD是∠BAC的平分线,
∴∠CAD=∠DAB.
又∵∠CAD+∠ADF=180°,
∴∠DAB+∠ADF=180°,
∴AB∥EF.
(2)∵AB∥EF,
∴∠ADE=∠DAB,∠CEF=∠BAC.
∵AD是∠BAC的平分线,
∴2∠DAB=∠BAC,
∴2∠ADE=∠CEF.
16.解:∵∠1+∠DFE=180°,∠1+∠2=180°,
∴∠DFE=∠2,
∴AB∥EF,
∴∠3=∠ADE.
∵∠ACB=∠AED,
∴DE∥BC,
∴∠B=∠ADE,
∴∠B=∠3.
17.解:如图,过点B作射线BE∥CD.
∵CD∥AF,
∴BE∥CD∥AF,
∴∠ABE=∠A=105°,
∴∠CBE=∠ABC-∠ABE=30°.
∵BE∥CD,
∴∠CBE+∠C=180°,
∴∠C=150°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
