七年级下册第一章 平行线 专题训练(一) 平行线中的“拐点”问题 练习(含解析)
文档属性
| 名称 | 七年级下册第一章 平行线 专题训练(一) 平行线中的“拐点”问题 练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 10:33:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题训练(一) 平行线中的“拐点”问题
【知识储备】
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)在解决几何问题时,有时需要添加辅助线,添加辅助线的过程要写入解题过程中,辅助线通常画成虚线.
【解题方法】
通常采用如下方法:
拐点个数 常用方法
一个 方法一:过拐点作其中一条直线的平行线,有几个拐点就作几条平行线 方法二:延长拐点处的角的一边
多个
类型之一 “”或“”形图
1.如图1-ZT-1,AB∥CD,∠A=105°,∠C=120°,求∠1的度数.
图1-ZT-1
2.如图1-ZT-2,已知AB∥CD,则∠α,∠β,∠γ之间的等量关系为 ( )
图1-ZT-2
A.∠α+∠β-∠γ=180°
B.∠β+∠γ-∠α=180°
C.∠α+∠β+∠γ=360°
D.∠α+∠β+∠γ=180°
类型之二 “”或“”形图
3.如图1-ZT-3,已知∠AEC=∠A+∠C,试说明:AB∥CD.
图1-ZT-3
4.如图1-ZT-4,AB∥CD,P为AB,CD之间的一点.已知∠1=32°,∠2=25°,求∠BPD的度数.
图1-ZT-4
类型之三 “”或“”形图
5.珠江流域某江段江水的流向经过B,C,D三点拐弯后与原来流向相同,如图1-ZT-5.若∠ABC=120°,∠BCD=80°,求∠CDE的度数.
图1-ZT-5
6.如图1-ZT-6,已知AB∥CD,∠ABE=135°,∠EDC=30°,求∠BED的度数.
图1-ZT-6
类型之四 多拐点型
7.如图1-ZT-7,AB∥CD,∠AEF=120°,∠EFC=90°,求∠A+∠C的度数.
图1-ZT-7
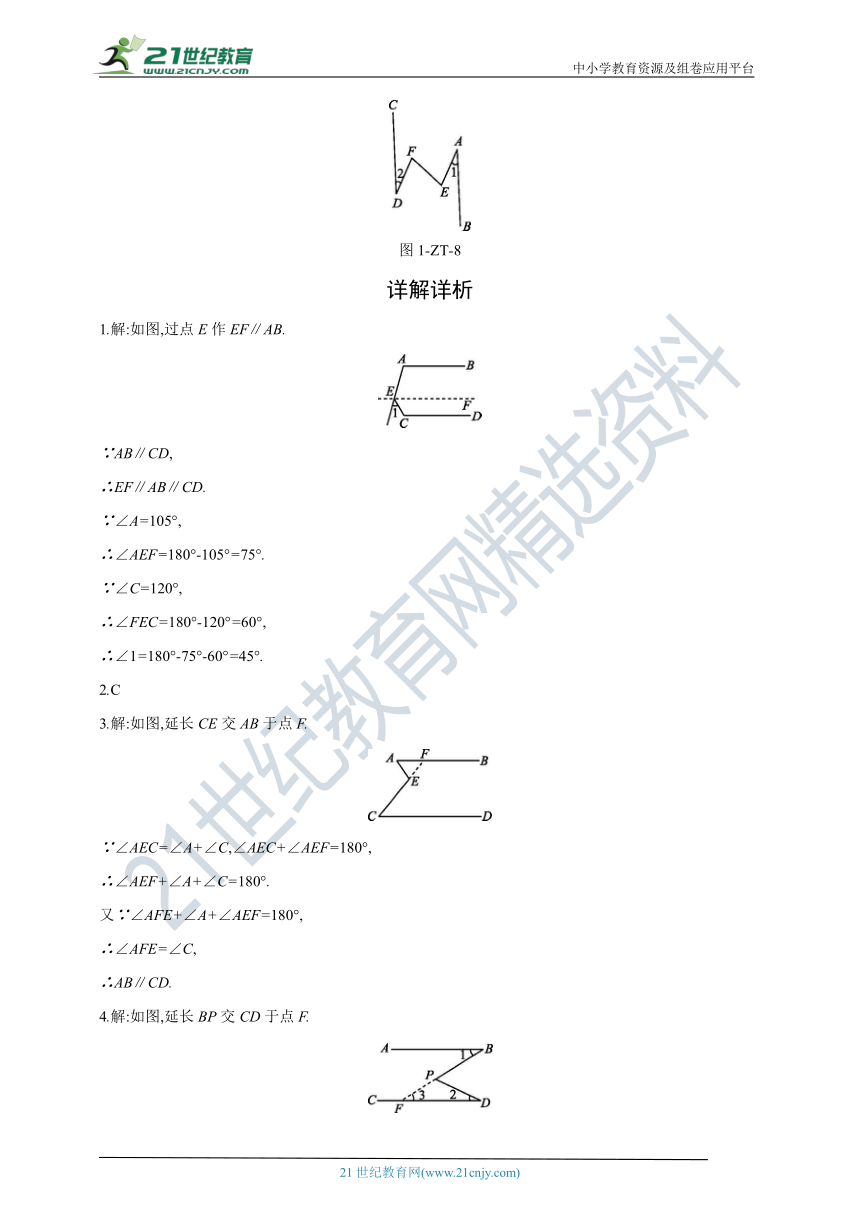
8.如图1-ZT-8,已知AB∥CD,∠1=∠2,试说明:∠E=∠F.
图1-ZT-8
详解详析
1.解:如图,过点E作EF∥AB.
∵AB∥CD,
∴EF∥AB∥CD.
∵∠A=105°,
∴∠AEF=180°-105°=75°.
∵∠C=120°,
∴∠FEC=180°-120°=60°,
∴∠1=180°-75°-60°=45°.
2.C
3.解:如图,延长CE交AB于点F.
∵∠AEC=∠A+∠C,∠AEC+∠AEF=180°,
∴∠AEF+∠A+∠C=180°.
又∵∠AFE+∠A+∠AEF=180°,
∴∠AFE=∠C,
∴AB∥CD.
4.解:如图,延长BP交CD于点F.
∵AB∥CD,
∴∠3=∠1=32°.
∵∠2=25°,
∴∠FPD=180°-25°-32°=123°,
∴∠BPD=180°-123°=57°.
5.解:由题意得AB∥DE.
如图,过点C作CF∥AB,则CF∥DE.
∵∠ABC=120°,
∴∠FCB=180°-120°=60°.
∵∠BCD=80°,
∴∠DCF=80°-60°=20°.
∵CF∥DE,
∴∠CDE=∠DCF=20°.
6.解:如图,延长BE交CD于点F.
∵AB∥CD,
∴∠ABE+∠BFD=180°.
∵∠ABE=135°,
∴∠BFD=45°.
∵∠BFD+∠EDC+∠DEF=180°,
∴∠DEF=105°,
∴∠BED=75°.
7.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵∠AEF=120°,∠EFC=90°,
∴∠AEG=60°,∠CFH=90°.
∵∠A+∠AEG+∠AGE=180°,∠C+∠CHF+∠CFH=180°,∠AGE+∠BGE=180°,∠CHF+∠FHD=180°,
∴∠A+∠AEG=∠BGE,∠C+∠CFH=∠FHD.
∵AB∥CD,
∴∠BGE+∠FHD=180°,
∴∠A+∠AEG+∠C+∠CFH=180°,
∴∠A+∠C=180°-∠AEG-∠CFH=180°-60°-90°=30°.
8.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵AB∥CD,
∴∠DHF=∠EGA.
∵∠1=∠2,
∴∠2+∠DHF=∠1+∠EGA.
∵∠2+∠DHF+∠DFH=180°,∠1+∠EGA+∠AEG=180°,∠DFH+∠DFE=180°,∠AEG+∠FEA=180°,
∴∠DFE=∠2+∠DHF,∠FEA=∠1+∠EGA,
∴∠DFE=∠FEA.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题训练(一) 平行线中的“拐点”问题
【知识储备】
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)在解决几何问题时,有时需要添加辅助线,添加辅助线的过程要写入解题过程中,辅助线通常画成虚线.
【解题方法】
通常采用如下方法:
拐点个数 常用方法
一个 方法一:过拐点作其中一条直线的平行线,有几个拐点就作几条平行线 方法二:延长拐点处的角的一边
多个
类型之一 “”或“”形图
1.如图1-ZT-1,AB∥CD,∠A=105°,∠C=120°,求∠1的度数.
图1-ZT-1
2.如图1-ZT-2,已知AB∥CD,则∠α,∠β,∠γ之间的等量关系为 ( )
图1-ZT-2
A.∠α+∠β-∠γ=180°
B.∠β+∠γ-∠α=180°
C.∠α+∠β+∠γ=360°
D.∠α+∠β+∠γ=180°
类型之二 “”或“”形图
3.如图1-ZT-3,已知∠AEC=∠A+∠C,试说明:AB∥CD.
图1-ZT-3
4.如图1-ZT-4,AB∥CD,P为AB,CD之间的一点.已知∠1=32°,∠2=25°,求∠BPD的度数.
图1-ZT-4
类型之三 “”或“”形图
5.珠江流域某江段江水的流向经过B,C,D三点拐弯后与原来流向相同,如图1-ZT-5.若∠ABC=120°,∠BCD=80°,求∠CDE的度数.
图1-ZT-5
6.如图1-ZT-6,已知AB∥CD,∠ABE=135°,∠EDC=30°,求∠BED的度数.
图1-ZT-6
类型之四 多拐点型
7.如图1-ZT-7,AB∥CD,∠AEF=120°,∠EFC=90°,求∠A+∠C的度数.
图1-ZT-7
8.如图1-ZT-8,已知AB∥CD,∠1=∠2,试说明:∠E=∠F.
图1-ZT-8
详解详析
1.解:如图,过点E作EF∥AB.
∵AB∥CD,
∴EF∥AB∥CD.
∵∠A=105°,
∴∠AEF=180°-105°=75°.
∵∠C=120°,
∴∠FEC=180°-120°=60°,
∴∠1=180°-75°-60°=45°.
2.C
3.解:如图,延长CE交AB于点F.
∵∠AEC=∠A+∠C,∠AEC+∠AEF=180°,
∴∠AEF+∠A+∠C=180°.
又∵∠AFE+∠A+∠AEF=180°,
∴∠AFE=∠C,
∴AB∥CD.
4.解:如图,延长BP交CD于点F.
∵AB∥CD,
∴∠3=∠1=32°.
∵∠2=25°,
∴∠FPD=180°-25°-32°=123°,
∴∠BPD=180°-123°=57°.
5.解:由题意得AB∥DE.
如图,过点C作CF∥AB,则CF∥DE.
∵∠ABC=120°,
∴∠FCB=180°-120°=60°.
∵∠BCD=80°,
∴∠DCF=80°-60°=20°.
∵CF∥DE,
∴∠CDE=∠DCF=20°.
6.解:如图,延长BE交CD于点F.
∵AB∥CD,
∴∠ABE+∠BFD=180°.
∵∠ABE=135°,
∴∠BFD=45°.
∵∠BFD+∠EDC+∠DEF=180°,
∴∠DEF=105°,
∴∠BED=75°.
7.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵∠AEF=120°,∠EFC=90°,
∴∠AEG=60°,∠CFH=90°.
∵∠A+∠AEG+∠AGE=180°,∠C+∠CHF+∠CFH=180°,∠AGE+∠BGE=180°,∠CHF+∠FHD=180°,
∴∠A+∠AEG=∠BGE,∠C+∠CFH=∠FHD.
∵AB∥CD,
∴∠BGE+∠FHD=180°,
∴∠A+∠AEG+∠C+∠CFH=180°,
∴∠A+∠C=180°-∠AEG-∠CFH=180°-60°-90°=30°.
8.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵AB∥CD,
∴∠DHF=∠EGA.
∵∠1=∠2,
∴∠2+∠DHF=∠1+∠EGA.
∵∠2+∠DHF+∠DFH=180°,∠1+∠EGA+∠AEG=180°,∠DFH+∠DFE=180°,∠AEG+∠FEA=180°,
∴∠DFE=∠2+∠DHF,∠FEA=∠1+∠EGA,
∴∠DFE=∠FEA.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
