1.4平行线的性质(2) 课件(共16张PPT)
文档属性
| 名称 | 1.4平行线的性质(2) 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 08:58:48 | ||
图片预览



文档简介
(共16张PPT)
1.4平行线的性质(2)
第1课时
浙教版 七年级下
新知导入
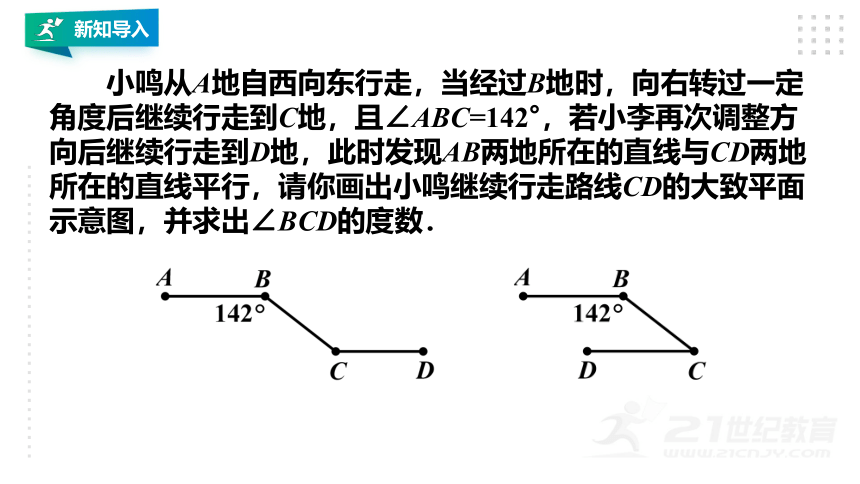
小鸣从A地自西向东行走,当经过B地时,向右转过一定角度后继续行走到C地,且∠ABC=142°,若小李再次调整方向后继续行走到D地,此时发现AB两地所在的直线与CD两地所在的直线平行,请你画出小鸣继续行走路线CD的大致平面示意图,并求出∠BCD的度数.
小鸣从A地自西向东行走,当经过B地时,向右转过一定角度后继续行走到C地,且∠ABC=142°,若小李再次调整方向后继续行走到D地,此时发现AB两地所在的直线与CD两地所在的直线平行,请你画出小鸣继续行走路线CD的大致平面示意图,并求出∠BCD的度数.
新知导入
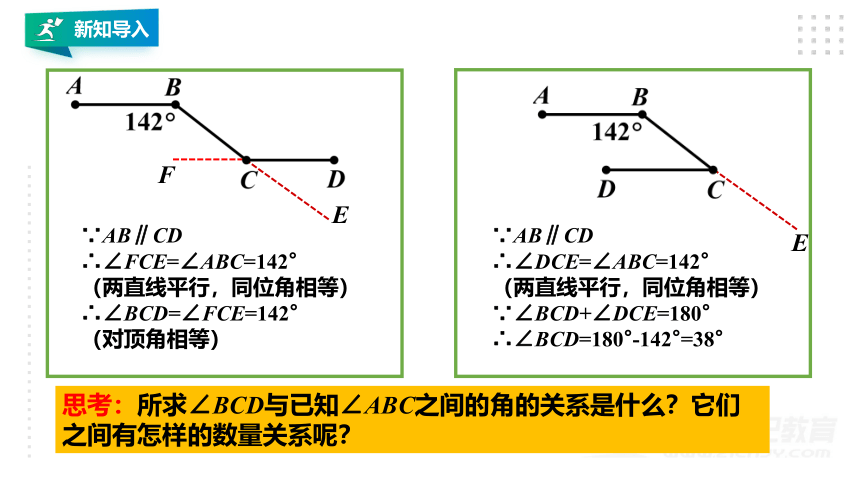
∵AB∥CD
∴∠FCE=∠ABC=142°
(两直线平行,同位角相等)
∴∠BCD=∠FCE=142°
(对顶角相等)
E
E
F
∵AB∥CD
∴∠DCE=∠ABC=142°
(两直线平行,同位角相等)
∵∠BCD+∠DCE=180°
∴∠BCD=180°-142°=38°
思考:所求∠BCD与已知∠ABC之间的角的关系是什么?它们之间有怎样的数量关系呢?
新知导入
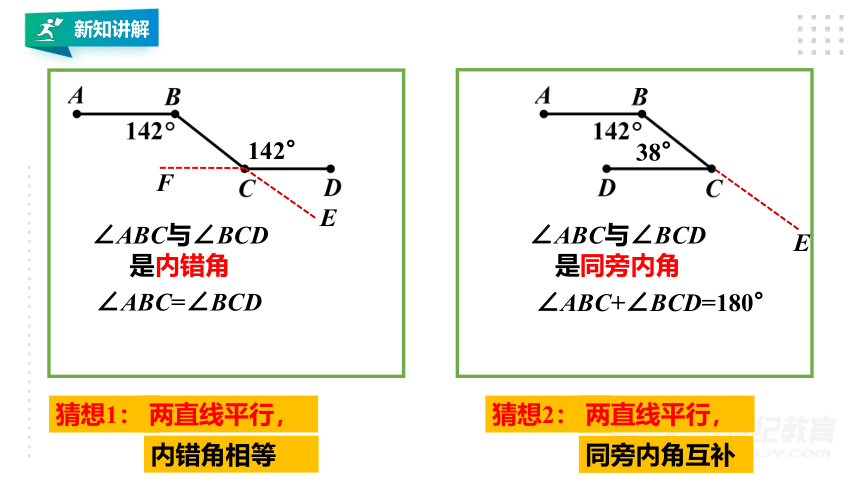
∠ABC与∠BCD是内错角
∠ABC+∠BCD=180°
∠ABC与∠BCD是同旁内角
∠ABC=∠BCD
猜想1:
同旁内角互补
两直线平行,
猜想2:
内错角相等
两直线平行,
E
F
142°
E
38°
新知讲解
验证1:
验证2:
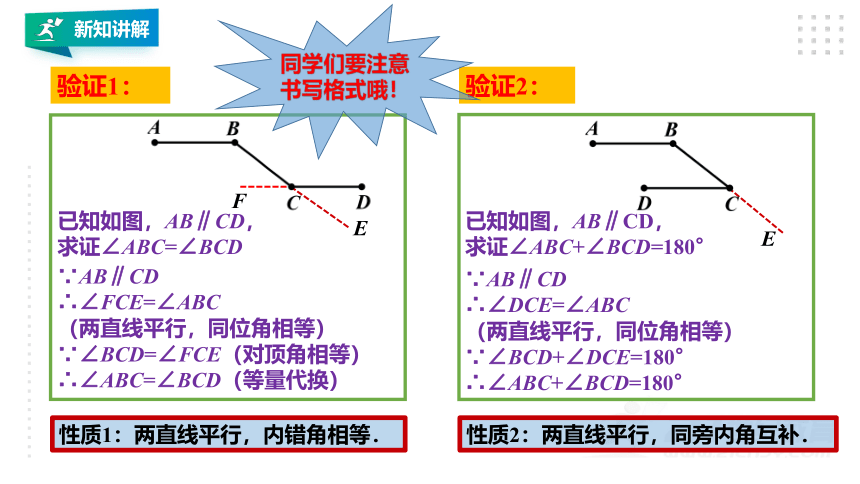
已知如图,AB∥CD,
求证∠ABC=∠BCD
∵AB∥CD
∴∠FCE=∠ABC
(两直线平行,同位角相等)
∵∠BCD=∠FCE(对顶角相等)∴∠ABC=∠BCD(等量代换)
E
已知如图,AB∥CD,
求证∠ABC+∠BCD=180°
∵AB∥CD
∴∠DCE=∠ABC
(两直线平行,同位角相等)
∵∠BCD+∠DCE=180°
∴∠ABC+∠BCD=180°
E
F
性质1:两直线平行,内错角相等.
性质2:两直线平行,同旁内角互补.
同学们要注意书写格式哦!
新知讲解
例题讲解
例3.如图,已知AB∥CD,AD∥BC.求证∠1=∠2.
分析
两个角之间的数量关系能直接求吗?
不能直接求
将角转移
与已知条件相结合
根据平行线的性质证明角相等
∵AB∥CD,∴∠3=∠1
(两直线平行,内错角相等)
∵AD∥BC,∴∠2=∠3
(两直线平行,同位角相等)
∴∠1=∠2(等量代换)
3
∵AB∥CD,∴∠1+∠4=180°
(两直线平行,同旁内角互补)
∵AD∥BC,∴∠2+∠4=180°
(两直线平行,同旁内角互补)
∴∠1=∠2(同角的补角相等)
同理可得:∠2+∠4=180°
4
例4.如图,已知∠ABC+∠C=180°,BD平分∠ABC.求证:∠CBD=∠D.
分析
∠CBD与∠D之间的数量关系能直接求吗?
将角转移
∠CBD=∠ABD
根据角平分线的性质
∠ABD与∠D是内错角
可以求
AB∥CD
有已知条件吗?
∠ABC+∠C=180°
∵∠ABC+∠C=180°
∴AB∥CD
(同旁内角互补,两直线平行)
∴∠ABD=∠D
(两直线平行,内错角相等)
∵BD平分∠ABC
∴∠CBD=∠ABD
∴∠CBD=∠D(等量代换)
∠ABD=∠D?
例题讲解
课堂练习
如图,是一条丝带末端的平面示意图,已知丝带两边AB∥CD,点E在AB,CD之间,形成了一个类似“W”形状,试求∠B,∠D与∠BED之间的数量关系.
课堂练习
如何书写?
分析
∠B,∠D与∠BED之间有直接联系吗?
将角转移
添加辅助线
何为辅助线?
1
2
过点E作MN∥AB
将添加的辅助线作为已知条件,继续推理
∵AB∥CD,MN∥AB
MN∥CD
平行线的传递性
∠B=∠1
∠D=∠2
M
N
∠BED=∠1+∠2
=∠B+∠D
如图,是一条丝带末端的平面示意图,已知丝带两边AB∥CD,点E在AB,CD之间,形成了一个类似“W”形状,试求∠B,∠D与∠BED之间的数量关系.
M
N
解:过点E作MN∥AB
∵AB∥CD,MN∥AB
MN∥AB∥CD(平行线的传递性)
∴∠B=∠1,∠D=∠2
(两直线平行,内错角相等)
∠BED=∠1+∠2=∠B+∠D(等量代换)
1
2
变式1:将丝带剪成形如“笔尖”一样的形状,试求∠B,∠D与∠BED之间的数量关系.
如图,是一条丝带末端的平面示意图,已知丝带两边AB∥CD,点E在AB,CD之间,形成了一个类似“W”形状,试求∠B,∠D与∠BED之间的数量关系.
课堂练习
课堂练习
变式2:
变式3:
课堂总结
今天对平行线的性质是不是有了新的认识
当两条平行直线被第三条直线所截时,
内错角相等,同旁内角互补.
平行线具有传递性
平行线的性质有什么用处呢?
证明角之间的数量关系或求角的大小
作业布置
作业本 1.4平行线的性质(2)
https://www.21cnjy.com/help/help_extract.php
1.4平行线的性质(2)
第1课时
浙教版 七年级下
新知导入
小鸣从A地自西向东行走,当经过B地时,向右转过一定角度后继续行走到C地,且∠ABC=142°,若小李再次调整方向后继续行走到D地,此时发现AB两地所在的直线与CD两地所在的直线平行,请你画出小鸣继续行走路线CD的大致平面示意图,并求出∠BCD的度数.
小鸣从A地自西向东行走,当经过B地时,向右转过一定角度后继续行走到C地,且∠ABC=142°,若小李再次调整方向后继续行走到D地,此时发现AB两地所在的直线与CD两地所在的直线平行,请你画出小鸣继续行走路线CD的大致平面示意图,并求出∠BCD的度数.
新知导入
∵AB∥CD
∴∠FCE=∠ABC=142°
(两直线平行,同位角相等)
∴∠BCD=∠FCE=142°
(对顶角相等)
E
E
F
∵AB∥CD
∴∠DCE=∠ABC=142°
(两直线平行,同位角相等)
∵∠BCD+∠DCE=180°
∴∠BCD=180°-142°=38°
思考:所求∠BCD与已知∠ABC之间的角的关系是什么?它们之间有怎样的数量关系呢?
新知导入
∠ABC与∠BCD是内错角
∠ABC+∠BCD=180°
∠ABC与∠BCD是同旁内角
∠ABC=∠BCD
猜想1:
同旁内角互补
两直线平行,
猜想2:
内错角相等
两直线平行,
E
F
142°
E
38°
新知讲解
验证1:
验证2:
已知如图,AB∥CD,
求证∠ABC=∠BCD
∵AB∥CD
∴∠FCE=∠ABC
(两直线平行,同位角相等)
∵∠BCD=∠FCE(对顶角相等)∴∠ABC=∠BCD(等量代换)
E
已知如图,AB∥CD,
求证∠ABC+∠BCD=180°
∵AB∥CD
∴∠DCE=∠ABC
(两直线平行,同位角相等)
∵∠BCD+∠DCE=180°
∴∠ABC+∠BCD=180°
E
F
性质1:两直线平行,内错角相等.
性质2:两直线平行,同旁内角互补.
同学们要注意书写格式哦!
新知讲解
例题讲解
例3.如图,已知AB∥CD,AD∥BC.求证∠1=∠2.
分析
两个角之间的数量关系能直接求吗?
不能直接求
将角转移
与已知条件相结合
根据平行线的性质证明角相等
∵AB∥CD,∴∠3=∠1
(两直线平行,内错角相等)
∵AD∥BC,∴∠2=∠3
(两直线平行,同位角相等)
∴∠1=∠2(等量代换)
3
∵AB∥CD,∴∠1+∠4=180°
(两直线平行,同旁内角互补)
∵AD∥BC,∴∠2+∠4=180°
(两直线平行,同旁内角互补)
∴∠1=∠2(同角的补角相等)
同理可得:∠2+∠4=180°
4
例4.如图,已知∠ABC+∠C=180°,BD平分∠ABC.求证:∠CBD=∠D.
分析
∠CBD与∠D之间的数量关系能直接求吗?
将角转移
∠CBD=∠ABD
根据角平分线的性质
∠ABD与∠D是内错角
可以求
AB∥CD
有已知条件吗?
∠ABC+∠C=180°
∵∠ABC+∠C=180°
∴AB∥CD
(同旁内角互补,两直线平行)
∴∠ABD=∠D
(两直线平行,内错角相等)
∵BD平分∠ABC
∴∠CBD=∠ABD
∴∠CBD=∠D(等量代换)
∠ABD=∠D?
例题讲解
课堂练习
如图,是一条丝带末端的平面示意图,已知丝带两边AB∥CD,点E在AB,CD之间,形成了一个类似“W”形状,试求∠B,∠D与∠BED之间的数量关系.
课堂练习
如何书写?
分析
∠B,∠D与∠BED之间有直接联系吗?
将角转移
添加辅助线
何为辅助线?
1
2
过点E作MN∥AB
将添加的辅助线作为已知条件,继续推理
∵AB∥CD,MN∥AB
MN∥CD
平行线的传递性
∠B=∠1
∠D=∠2
M
N
∠BED=∠1+∠2
=∠B+∠D
如图,是一条丝带末端的平面示意图,已知丝带两边AB∥CD,点E在AB,CD之间,形成了一个类似“W”形状,试求∠B,∠D与∠BED之间的数量关系.
M
N
解:过点E作MN∥AB
∵AB∥CD,MN∥AB
MN∥AB∥CD(平行线的传递性)
∴∠B=∠1,∠D=∠2
(两直线平行,内错角相等)
∠BED=∠1+∠2=∠B+∠D(等量代换)
1
2
变式1:将丝带剪成形如“笔尖”一样的形状,试求∠B,∠D与∠BED之间的数量关系.
如图,是一条丝带末端的平面示意图,已知丝带两边AB∥CD,点E在AB,CD之间,形成了一个类似“W”形状,试求∠B,∠D与∠BED之间的数量关系.
课堂练习
课堂练习
变式2:
变式3:
课堂总结
今天对平行线的性质是不是有了新的认识
当两条平行直线被第三条直线所截时,
内错角相等,同旁内角互补.
平行线具有传递性
平行线的性质有什么用处呢?
证明角之间的数量关系或求角的大小
作业布置
作业本 1.4平行线的性质(2)
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
