2021--2022学年浙教版七年级数学下册2.4 二元一次方程组的应用 同步练习(word版 含解析)
文档属性
| 名称 | 2021--2022学年浙教版七年级数学下册2.4 二元一次方程组的应用 同步练习(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览




文档简介
二元一次方程组的应用同步练习
一、单选题
1.明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问君多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )
A. B.
C. D.
2.一种饮料有两种包装,2大盒、4小盒共装88瓶,3大盒、2小盒共装84瓶,大盒与小盒每盒各装多少瓶?设大盒装x瓶,小盒装y瓶,则可列方程组( )
A. B.
C. D.
3.小明打算购买气球装扮“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图,则第三束气球的价格为( )
A.16 B.15 C.14 D.13
4.《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )
A. B.
C. D.
5.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架,其中《磁不足》卷记载了一道有趣的数学问题:“今有共买物,人出八,赢三;人出七,不足四,问人数、物价各几何?”译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱,问人数,物价各多少?”设人数为x人,物价为y钱,根据题意,下面所列方程组正确的是( )
A. B.
C. D.
6.甲、乙两人做同样的零件,如果甲先做1天,乙再开始做,5天后两人做的一样多;如果甲先做30个,乙再开始做,4天后乙反而比甲多做10个,设甲每天做 个,乙每天做 个,则可列出的方程组是( )
A. B.
C. D.
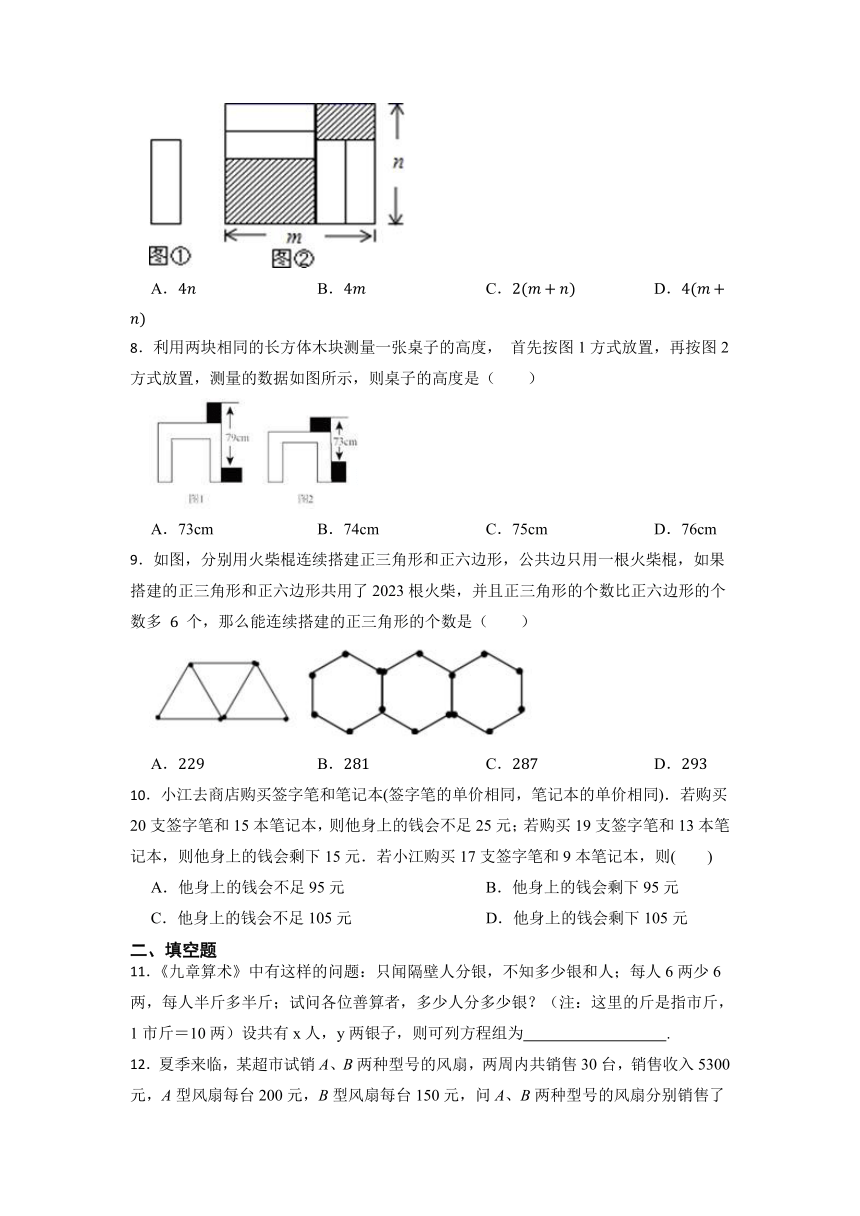
7.把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A. B. C. D.
8.利用两块相同的长方体木块测量一张桌子的高度, 首先按图1方式放置,再按图2方式放置,测量的数据如图所示,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
9.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多 个,那么能连续搭建的正三角形的个数是( )
A. B. C. D.
10.小江去商店购买签字笔和笔记本(签字笔的单价相同,笔记本的单价相同).若购买20支签字笔和15本笔记本,则他身上的钱会不足25元;若购买19支签字笔和13本笔记本,则他身上的钱会剩下15元.若小江购买17支签字笔和9本笔记本,则( )
A.他身上的钱会不足95元 B.他身上的钱会剩下95元
C.他身上的钱会不足105元 D.他身上的钱会剩下105元
二、填空题
11.《九章算术》中有这样的问题:只闻隔壁人分银,不知多少银和人;每人6两少6两,每人半斤多半斤;试问各位善算者,多少人分多少银?(注:这里的斤是指市斤,1市斤=10两)设共有x人,y两银子,则可列方程组为 .
12.夏季来临,某超市试销A、B两种型号的风扇,两周内共销售30台,销售收入5300元,A型风扇每台200元,B型风扇每台150元,问A、B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组 .
13.假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过 小时车库恰好停满.
14.从A城到B城的航线长1200 km,一架飞机从A城飞往B城,需要2 h,从B城飞往A城,需要2.5 h,假设飞机保持匀速,风速的大小和方向不变,设飞机的速度为 千米/小时,风速为 千米/小时,则可列方程组为: .
15.用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是 .
16.若关于 , 的方程组 的解是 则关于 , 的方程组 的解是 .
17.随着电影《流浪地球》的热映,科幻大神刘慈欣的著作受到广大书迷的追捧,《流浪地球》《球状闪电》《三体》《超新星纪元》四部小说在某网上书城热销.已知《流浪地球》的销售单价与《球状闪电》相同,《三体》的销售单价是《超新星纪元》单价的3倍,《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;若自电影上映以来,《流浪地球》与《超新星纪元》的日销售量相同,《球状闪电》的日销售量为《三体》日销售量的3倍,《流浪地球》与《三体》的日销售量和为450本,且《流浪地球》的日销售量不低于《三体》的日销量的 且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为 元.
18.某运输公司有核定载重量之比为 的甲、乙、丙三种货车,该运输公司接到为某灾区免费运输物资任务,迅速按照各车型核定载重量将物资运往灾区,承担本次运输的三种货车数量相同,当这批物资送达灾区后,发现还需要一部分物资才能满足当地灾区的需要,于是该运输公司又安排部分甲、乙丙三种货车进行第二次运输,其中乙型车第二次送输的物资量是还需要运输的物资量的 ,丙型车两次运输的物资总量是两次运往灾区物资总量的 ,甲型车两次运输的物资总量与乙型车两次运输的物总量之比为 ,则甲型车第一次与甲型车第二次运输的物资量之比是 .
三、解答题
19.A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度.(用方程解)
20.某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些地产土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如表:
作物种类 每公顷所需人数/人 每公顷投入资金/万元
蔬菜 4 2
水果 5 3
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
21.用8块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示,求矩形地面的面积?
22.食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A、B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,饮料加工厂生产了A、B两种饮料各多少瓶?
23.甲乙两人以不变的速度在环形路上跑步,相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,已知甲比乙跑的快,求甲、乙两人每分钟各跑多少圈?
24.某工厂的一条流水线匀速生产出产品,在有一些产品积压的情况下,经过试验,若安排9人包装,则5小时可以包装完所有产品;若安排6人包装,则需要10小时才能包装完所有产品.假设每个人的包装速度一样,现要在2小时内完成产品包装的任务,问至少需要安排多少人?
答案解析部分
1.【答案】B
【解析】【解答】解:设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根 ,根据题意有
故答案为:B
【分析】本题第一个数量关系:共有83000根短竹,所以x+y=83000;第二个数量关系毛管数=笔套数,即3x=5y;联立两个方程即可得到答案.
2.【答案】A
【解析】【解答】解:设大盒装x瓶,小盒装y瓶,根据题意可列方程组为: ,
故答案为:A.
【分析】根据“大盒的数量×x+小盒的数量×y=总瓶数”分别列方程,联立可得方程组.
3.【答案】C
【解析】【解答】设一个笑脸气球x元,一个爱心气球y元,则
解得
所以2x+2y=14
所以第三束气球是14元;
故答案为:C
【分析】设一个笑脸气球x元,一个爱心气球y元,则 ,解方程组,求出2x+2y即可.
4.【答案】D
【解析】【解答】第一个方程 的系数为2, 的系数为1,相加的结果为11;第二个方程 的系数为4, 的系数为3,相加的结果为27,所以可列方程组为: .
故答案为:D.
【分析】根据第一个方程 x 的系数为2, y 的系数为1,相加的结果为11;第二个方程 x 的系数为4, y 的系数为3,相加的结果为27,列方程组即可。
5.【答案】B
【解析】【解答】解:由题意可得, ,
故答案为:B.
【分析】根据译文可知“人数×8-3=钱数和人数×7+4=钱数”即可列出方程组.
6.【答案】B
【解析】【解答】设甲每天做 个,乙每天做 个,根据如果甲先做1天,乙再开始做,5天后两人做的一样多;如果甲先做30个,乙再开始做,4天后乙反而比甲多做10个,
可得方程组
故答案为:B.
【分析】设甲每天做 个,乙每天做 个,根据题意即可列出方程组.
7.【答案】A
【解析】【解答】设小长方形的长为a,宽为b,
上面的长方形周长:2(m-a+n-a),下面的长方形周长:2(m-2b+n-2b),
两式联立,总周长为:2(m-a+n-a)+2(m-2b+n-2b)=4m+4n-4(a+2b),
∵a+2b=m(由图可得),
∴阴影部分总周长为4m+4n-4(a+2b)=4m+4n-4m=4n.
故答案为:A.
【分析】设小长方形长为x,宽为y,根据图形求出3y+x=7,表示出阴影部分周长之和即可。
8.【答案】D
【解析】【解答】设长方体长xcm,宽ycm,桌子的高为acm,由题意得两式相加得:2a=152,解得a=76。
故答案为:D
【分析】设长方体长xcm,宽ycm,桌子的高为acm,分析图像建立方程组求出解就可以得出桌子高度。
9.【答案】D
【解析】【解答】解:设连续搭建正三角形的个数为x个,连续搭建正六边形的个数为y个,
由题意得:,
解得:.
故答案为:D.
【分析】设连续搭建正三角形的个数为x个,连续搭建正六边形的个数为y个,看图可知,连续搭建正三角形所用的火柴为2x+1个,连续搭建正六边形所用的火柴为5y+1个,然后根据“正三角形的个数比正六边形的个数多 个和搭建的正三角形和正六边形共用了2023根火柴”,分别列方程,联立求解即可。
10.【答案】B
【解析】【解答】解设签字笔单价为a ,笔记本的单价为b,他身上带的钱为m, 则m=20a+15b-25, m=19a+13b+15;
20a+15b-25=19a+13b+15, 得a+2b=40, 则17a+9b=19a+13b-2a-4b=m-15-2(a+2b)=m-15-80=m-95;
故答案为:B
【分析】本题需设几个未知量,但设而不求,用整体变形和代换求出具体数据,这是很实用的一种方法。
11.【答案】
【解析】【解答】解:设共有x人,y两银子,则可列方程组为:
.
故答案为: .
【分析】根据题意“每人6两少6两,每人半斤多半斤”可以列出相应的方程组,从而得出答案.
12.【答案】
【解析】【解答】解:设A型风扇销售了x台,B型风扇销售了y台,
依题意,得: .
故答案为: .
【分析】设A型风扇销售了x台,B型风扇销售了y台,根据总价=单价×数量结合销售A、B两种型号的风扇30台收入5300元,即可得出关于x,y的二元一次方程组,此题得解.
13.【答案】
【解析】【解答】设1个进口1小时开进x辆车,1个出口1小时开出y辆,车位总数为a,由题意得:
解得: .
则60%a÷(2x-y)=60%a÷( a×2 a)= (小时).
故答案为: .
【分析】设1个进口1小时开进x辆车,1个出口1小时开出y辆,车位总数为a,根据开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满列出方程组,解方程组求出x,y,再根据车位总数÷(开进车辆-开出车辆)= 恰好停满所用的时间求出即可.
14.【答案】
【解析】【解答】根据题意列出方程组
【分析】找到等量关系式,路程=速度×时间 ,列出方程组即可
15.【答案】9
【解析】【解答】∵图1所示的正方形其涂色部分的面积是25,图2所示的正方形其涂色部分的面积是16
∴图1涂色的正方形边长为5,图2涂色的正方形边长为4,
设长方形纸片的长为x,宽为y,根据题意有
解得
∴图3涂色的正方形的边长为 ,面积为
故答案为:9.
【分析】设长方形纸片的长为x,宽为y,根据题意列出方程组求出x,y的值,则图3的涂色部分的边长可求,进而面积可求.
16.【答案】
【解析】【解答】设 , ,
则原方程组可化为 ,
∵关于 , 的方程组 的解是 ,
∴ ,
∴ ,即 ,
∴关于 , 的方程组 的解是 ;
故答案是 .
【分析】本题考查了用换元法解二元一次方程组,根据后面所给的方程可以用换元法,将x+2设为m,y-1设为n,从而得出构成了关于m,n的值,继而求出x,y的值,本题也可以运用整体思想进行求解.
17.【答案】23.75
【解析】【解答】解:设《流浪地球》的单价为m元/本,《超新星纪元》单价为n元/本,则《球状闪电》的单价也为m元/本,《三体》的单价为3n元/本,
设《流浪地球》的销售量为a本,《三体》的销售量为b本,则《超新星纪元》的销售量为a本,《球状闪电》的销售量为3b本,
单价、数量、总价之间的关系可用下表表示:
∵《流浪地球》与《三体》的日销售量和为450本,
∴a+b=450,即,b=450﹣a,
∴《流浪地球》的日销售量不低于《三体》的日销量的 且小于230本,
∴a≥ b,a<230,b=450﹣a,
∴180≤a<230,
又∵《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;
∴40<m+n≤50,
∵《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.
∴ma+n(1350﹣3a)=m(1350﹣3a)+na+1575,
即:(m﹣n)(4a﹣1350)=1575,
∵180≤a<230,
∴4a﹣1350<0,
∴m﹣n<0,即m<n,
当《流浪地球》《三体》这2部小说日销额之和最多时,即ma+n(1350﹣3a)= [ma+n(1350﹣3a)+m(1350﹣3a)+na+1575]= 最大
即 和 最大,
∵a的最小值为180,代入(m﹣n)(4a﹣1350)=1575,得,
m﹣n=﹣ ,即n=m+ ,
又∵40<m+n≤50,
∴m+n的最大值为50
解得:m= ,
故答案为: .
【分析】设出未知数,表示四部小说的单价、数量、总价,分别根据题意,列出相应的方程或不等式,确定未知数的值,或未知数的取值范围,最后根据“当《流浪地球》《三体》这2部小说日销额之和最多时”求出相应的《流浪地球》的单价即可.
18.【答案】
【解析】【解答】解:设第一次甲种货车运输的总重量为3x,乙种货车运输的总重量为4x,丙种货车运输的总重量为5x,第二次三种货车运输的总重量为y,根据题意得,
第二次乙种货车运输的总重量为 y,
第二次甲种货车运输的总重量为 (4x+ y)-3x= ,
第二次丙种货车运输的总重量为 ,
于是有: y + + =y,
∴y= x,
∴甲型车第一次与第二次运输的物资量之比:3x:( )= .
故答案为: .
【分析】设第一次甲种、乙种、丙种货车运输的总重量分别为3x、4x、5x,第二次三种货车运输的总重量为y,根据题意分别表示出第二次甲种、乙种、丙种货车分别运输的总重量,列出关于x、y的二元一次方程,然后表示出y,进而求出甲型车第一次与第二次运输的物资量之比.
19.【答案】解:设甲的速度为x千米/时,乙的速度为y千米/时,
依题意得: ,
解得: .
答:甲的速度为4千米/时,乙的速度为5千米/时.
【解析】【分析】设甲的速度为x千米/时,乙的速度为y千米/时,依题意得:4x+4y=36,36-6x=2(36-6y),联立求解即可.
20.【答案】解:设承包的田地中,x公顷种蔬菜,y公顷种水果,
根据题意得: ,
解得: .
x+y=2.5+1=3.5(公顷)
答:应承包3.5公顷土地,其中2.5公顷种蔬菜,1公顷种水果.
【解析】【分析】设承包的田地中,x公顷种蔬菜,y公顷种水果,根据每公顷所需人数与每公顷投入资金数可把总人数与总资金用x,y表示出来,由此可得到关于x、y的两个方程;联立方程组即可求出x、y的值,即可得答案.
21.【答案】解:设每块地砖的长为xcm,宽为ycm,
根据题意得
解这个方程组,得
45×15×8=5400
【解析】【分析】设每块地砖的长为xcm,宽为ycm,观察图形中拼图可得等量x+y=60.x=3y,据此列出方程组,解出即可.
22.【答案】解:设甲种饮料 瓶,乙种饮料 瓶,
由题意得
解之得
答:生产甲饮料40瓶,乙饮料60瓶
【解析】【分析】本题是二元一次方程组的应用,设甲种饮料 x 瓶,乙种饮料 y 瓶,根据题意列出方程组即可.
23.【答案】解:设甲每分跑x圈,乙每分跑y圈,
根据题意得: ,
解得: .
则甲、乙二人每分各跑 圈与 圈.
【解析】【分析】由题意可知,题中关键的已知条件为:相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,隐含了两个等量关系,然后设未知数,列方程组,然后求出方程组的解。
24.【答案】解:设原有产品m,每个人的包装速度为x,每小时流水线生产的产品为y.
则 ,解得:
若需要n人刚好完成,则2nx=m+y,
∴至少需要18人
【解析】【分析】 设原有产品m,每个人的包装速度为x,每小时流水线生产的产品为y,根据两种方法包装这批产品,总量不变列出方程组,进而即可求出.
一、单选题
1.明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问君多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )
A. B.
C. D.
2.一种饮料有两种包装,2大盒、4小盒共装88瓶,3大盒、2小盒共装84瓶,大盒与小盒每盒各装多少瓶?设大盒装x瓶,小盒装y瓶,则可列方程组( )
A. B.
C. D.
3.小明打算购买气球装扮“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图,则第三束气球的价格为( )
A.16 B.15 C.14 D.13
4.《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )
A. B.
C. D.
5.《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架,其中《磁不足》卷记载了一道有趣的数学问题:“今有共买物,人出八,赢三;人出七,不足四,问人数、物价各几何?”译文:“今有人合伙购物,每人出8钱,会多出3钱;每人出7钱,又差4钱,问人数,物价各多少?”设人数为x人,物价为y钱,根据题意,下面所列方程组正确的是( )
A. B.
C. D.
6.甲、乙两人做同样的零件,如果甲先做1天,乙再开始做,5天后两人做的一样多;如果甲先做30个,乙再开始做,4天后乙反而比甲多做10个,设甲每天做 个,乙每天做 个,则可列出的方程组是( )
A. B.
C. D.
7.把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A. B. C. D.
8.利用两块相同的长方体木块测量一张桌子的高度, 首先按图1方式放置,再按图2方式放置,测量的数据如图所示,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
9.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多 个,那么能连续搭建的正三角形的个数是( )
A. B. C. D.
10.小江去商店购买签字笔和笔记本(签字笔的单价相同,笔记本的单价相同).若购买20支签字笔和15本笔记本,则他身上的钱会不足25元;若购买19支签字笔和13本笔记本,则他身上的钱会剩下15元.若小江购买17支签字笔和9本笔记本,则( )
A.他身上的钱会不足95元 B.他身上的钱会剩下95元
C.他身上的钱会不足105元 D.他身上的钱会剩下105元
二、填空题
11.《九章算术》中有这样的问题:只闻隔壁人分银,不知多少银和人;每人6两少6两,每人半斤多半斤;试问各位善算者,多少人分多少银?(注:这里的斤是指市斤,1市斤=10两)设共有x人,y两银子,则可列方程组为 .
12.夏季来临,某超市试销A、B两种型号的风扇,两周内共销售30台,销售收入5300元,A型风扇每台200元,B型风扇每台150元,问A、B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组 .
13.假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过 小时车库恰好停满.
14.从A城到B城的航线长1200 km,一架飞机从A城飞往B城,需要2 h,从B城飞往A城,需要2.5 h,假设飞机保持匀速,风速的大小和方向不变,设飞机的速度为 千米/小时,风速为 千米/小时,则可列方程组为: .
15.用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是 .
16.若关于 , 的方程组 的解是 则关于 , 的方程组 的解是 .
17.随着电影《流浪地球》的热映,科幻大神刘慈欣的著作受到广大书迷的追捧,《流浪地球》《球状闪电》《三体》《超新星纪元》四部小说在某网上书城热销.已知《流浪地球》的销售单价与《球状闪电》相同,《三体》的销售单价是《超新星纪元》单价的3倍,《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;若自电影上映以来,《流浪地球》与《超新星纪元》的日销售量相同,《球状闪电》的日销售量为《三体》日销售量的3倍,《流浪地球》与《三体》的日销售量和为450本,且《流浪地球》的日销售量不低于《三体》的日销量的 且小于230本;《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.则当《流浪地球》《三体》这2部小说日销额之和最多时,《流浪地球》的单价为 元.
18.某运输公司有核定载重量之比为 的甲、乙、丙三种货车,该运输公司接到为某灾区免费运输物资任务,迅速按照各车型核定载重量将物资运往灾区,承担本次运输的三种货车数量相同,当这批物资送达灾区后,发现还需要一部分物资才能满足当地灾区的需要,于是该运输公司又安排部分甲、乙丙三种货车进行第二次运输,其中乙型车第二次送输的物资量是还需要运输的物资量的 ,丙型车两次运输的物资总量是两次运往灾区物资总量的 ,甲型车两次运输的物资总量与乙型车两次运输的物总量之比为 ,则甲型车第一次与甲型车第二次运输的物资量之比是 .
三、解答题
19.A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度.(用方程解)
20.某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些地产土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如表:
作物种类 每公顷所需人数/人 每公顷投入资金/万元
蔬菜 4 2
水果 5 3
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
21.用8块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示,求矩形地面的面积?
22.食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A、B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,饮料加工厂生产了A、B两种饮料各多少瓶?
23.甲乙两人以不变的速度在环形路上跑步,相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,已知甲比乙跑的快,求甲、乙两人每分钟各跑多少圈?
24.某工厂的一条流水线匀速生产出产品,在有一些产品积压的情况下,经过试验,若安排9人包装,则5小时可以包装完所有产品;若安排6人包装,则需要10小时才能包装完所有产品.假设每个人的包装速度一样,现要在2小时内完成产品包装的任务,问至少需要安排多少人?
答案解析部分
1.【答案】B
【解析】【解答】解:设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根 ,根据题意有
故答案为:B
【分析】本题第一个数量关系:共有83000根短竹,所以x+y=83000;第二个数量关系毛管数=笔套数,即3x=5y;联立两个方程即可得到答案.
2.【答案】A
【解析】【解答】解:设大盒装x瓶,小盒装y瓶,根据题意可列方程组为: ,
故答案为:A.
【分析】根据“大盒的数量×x+小盒的数量×y=总瓶数”分别列方程,联立可得方程组.
3.【答案】C
【解析】【解答】设一个笑脸气球x元,一个爱心气球y元,则
解得
所以2x+2y=14
所以第三束气球是14元;
故答案为:C
【分析】设一个笑脸气球x元,一个爱心气球y元,则 ,解方程组,求出2x+2y即可.
4.【答案】D
【解析】【解答】第一个方程 的系数为2, 的系数为1,相加的结果为11;第二个方程 的系数为4, 的系数为3,相加的结果为27,所以可列方程组为: .
故答案为:D.
【分析】根据第一个方程 x 的系数为2, y 的系数为1,相加的结果为11;第二个方程 x 的系数为4, y 的系数为3,相加的结果为27,列方程组即可。
5.【答案】B
【解析】【解答】解:由题意可得, ,
故答案为:B.
【分析】根据译文可知“人数×8-3=钱数和人数×7+4=钱数”即可列出方程组.
6.【答案】B
【解析】【解答】设甲每天做 个,乙每天做 个,根据如果甲先做1天,乙再开始做,5天后两人做的一样多;如果甲先做30个,乙再开始做,4天后乙反而比甲多做10个,
可得方程组
故答案为:B.
【分析】设甲每天做 个,乙每天做 个,根据题意即可列出方程组.
7.【答案】A
【解析】【解答】设小长方形的长为a,宽为b,
上面的长方形周长:2(m-a+n-a),下面的长方形周长:2(m-2b+n-2b),
两式联立,总周长为:2(m-a+n-a)+2(m-2b+n-2b)=4m+4n-4(a+2b),
∵a+2b=m(由图可得),
∴阴影部分总周长为4m+4n-4(a+2b)=4m+4n-4m=4n.
故答案为:A.
【分析】设小长方形长为x,宽为y,根据图形求出3y+x=7,表示出阴影部分周长之和即可。
8.【答案】D
【解析】【解答】设长方体长xcm,宽ycm,桌子的高为acm,由题意得两式相加得:2a=152,解得a=76。
故答案为:D
【分析】设长方体长xcm,宽ycm,桌子的高为acm,分析图像建立方程组求出解就可以得出桌子高度。
9.【答案】D
【解析】【解答】解:设连续搭建正三角形的个数为x个,连续搭建正六边形的个数为y个,
由题意得:,
解得:.
故答案为:D.
【分析】设连续搭建正三角形的个数为x个,连续搭建正六边形的个数为y个,看图可知,连续搭建正三角形所用的火柴为2x+1个,连续搭建正六边形所用的火柴为5y+1个,然后根据“正三角形的个数比正六边形的个数多 个和搭建的正三角形和正六边形共用了2023根火柴”,分别列方程,联立求解即可。
10.【答案】B
【解析】【解答】解设签字笔单价为a ,笔记本的单价为b,他身上带的钱为m, 则m=20a+15b-25, m=19a+13b+15;
20a+15b-25=19a+13b+15, 得a+2b=40, 则17a+9b=19a+13b-2a-4b=m-15-2(a+2b)=m-15-80=m-95;
故答案为:B
【分析】本题需设几个未知量,但设而不求,用整体变形和代换求出具体数据,这是很实用的一种方法。
11.【答案】
【解析】【解答】解:设共有x人,y两银子,则可列方程组为:
.
故答案为: .
【分析】根据题意“每人6两少6两,每人半斤多半斤”可以列出相应的方程组,从而得出答案.
12.【答案】
【解析】【解答】解:设A型风扇销售了x台,B型风扇销售了y台,
依题意,得: .
故答案为: .
【分析】设A型风扇销售了x台,B型风扇销售了y台,根据总价=单价×数量结合销售A、B两种型号的风扇30台收入5300元,即可得出关于x,y的二元一次方程组,此题得解.
13.【答案】
【解析】【解答】设1个进口1小时开进x辆车,1个出口1小时开出y辆,车位总数为a,由题意得:
解得: .
则60%a÷(2x-y)=60%a÷( a×2 a)= (小时).
故答案为: .
【分析】设1个进口1小时开进x辆车,1个出口1小时开出y辆,车位总数为a,根据开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满列出方程组,解方程组求出x,y,再根据车位总数÷(开进车辆-开出车辆)= 恰好停满所用的时间求出即可.
14.【答案】
【解析】【解答】根据题意列出方程组
【分析】找到等量关系式,路程=速度×时间 ,列出方程组即可
15.【答案】9
【解析】【解答】∵图1所示的正方形其涂色部分的面积是25,图2所示的正方形其涂色部分的面积是16
∴图1涂色的正方形边长为5,图2涂色的正方形边长为4,
设长方形纸片的长为x,宽为y,根据题意有
解得
∴图3涂色的正方形的边长为 ,面积为
故答案为:9.
【分析】设长方形纸片的长为x,宽为y,根据题意列出方程组求出x,y的值,则图3的涂色部分的边长可求,进而面积可求.
16.【答案】
【解析】【解答】设 , ,
则原方程组可化为 ,
∵关于 , 的方程组 的解是 ,
∴ ,
∴ ,即 ,
∴关于 , 的方程组 的解是 ;
故答案是 .
【分析】本题考查了用换元法解二元一次方程组,根据后面所给的方程可以用换元法,将x+2设为m,y-1设为n,从而得出构成了关于m,n的值,继而求出x,y的值,本题也可以运用整体思想进行求解.
17.【答案】23.75
【解析】【解答】解:设《流浪地球》的单价为m元/本,《超新星纪元》单价为n元/本,则《球状闪电》的单价也为m元/本,《三体》的单价为3n元/本,
设《流浪地球》的销售量为a本,《三体》的销售量为b本,则《超新星纪元》的销售量为a本,《球状闪电》的销售量为3b本,
单价、数量、总价之间的关系可用下表表示:
∵《流浪地球》与《三体》的日销售量和为450本,
∴a+b=450,即,b=450﹣a,
∴《流浪地球》的日销售量不低于《三体》的日销量的 且小于230本,
∴a≥ b,a<230,b=450﹣a,
∴180≤a<230,
又∵《流浪地球》与《超新星纪元》的单价和大于40元且不超过50元;
∴40<m+n≤50,
∵《流浪地球》《三体》的日销量额之和比《球状闪电》《超新星纪元》的日销售额之和多1575元.
∴ma+n(1350﹣3a)=m(1350﹣3a)+na+1575,
即:(m﹣n)(4a﹣1350)=1575,
∵180≤a<230,
∴4a﹣1350<0,
∴m﹣n<0,即m<n,
当《流浪地球》《三体》这2部小说日销额之和最多时,即ma+n(1350﹣3a)= [ma+n(1350﹣3a)+m(1350﹣3a)+na+1575]= 最大
即 和 最大,
∵a的最小值为180,代入(m﹣n)(4a﹣1350)=1575,得,
m﹣n=﹣ ,即n=m+ ,
又∵40<m+n≤50,
∴m+n的最大值为50
解得:m= ,
故答案为: .
【分析】设出未知数,表示四部小说的单价、数量、总价,分别根据题意,列出相应的方程或不等式,确定未知数的值,或未知数的取值范围,最后根据“当《流浪地球》《三体》这2部小说日销额之和最多时”求出相应的《流浪地球》的单价即可.
18.【答案】
【解析】【解答】解:设第一次甲种货车运输的总重量为3x,乙种货车运输的总重量为4x,丙种货车运输的总重量为5x,第二次三种货车运输的总重量为y,根据题意得,
第二次乙种货车运输的总重量为 y,
第二次甲种货车运输的总重量为 (4x+ y)-3x= ,
第二次丙种货车运输的总重量为 ,
于是有: y + + =y,
∴y= x,
∴甲型车第一次与第二次运输的物资量之比:3x:( )= .
故答案为: .
【分析】设第一次甲种、乙种、丙种货车运输的总重量分别为3x、4x、5x,第二次三种货车运输的总重量为y,根据题意分别表示出第二次甲种、乙种、丙种货车分别运输的总重量,列出关于x、y的二元一次方程,然后表示出y,进而求出甲型车第一次与第二次运输的物资量之比.
19.【答案】解:设甲的速度为x千米/时,乙的速度为y千米/时,
依题意得: ,
解得: .
答:甲的速度为4千米/时,乙的速度为5千米/时.
【解析】【分析】设甲的速度为x千米/时,乙的速度为y千米/时,依题意得:4x+4y=36,36-6x=2(36-6y),联立求解即可.
20.【答案】解:设承包的田地中,x公顷种蔬菜,y公顷种水果,
根据题意得: ,
解得: .
x+y=2.5+1=3.5(公顷)
答:应承包3.5公顷土地,其中2.5公顷种蔬菜,1公顷种水果.
【解析】【分析】设承包的田地中,x公顷种蔬菜,y公顷种水果,根据每公顷所需人数与每公顷投入资金数可把总人数与总资金用x,y表示出来,由此可得到关于x、y的两个方程;联立方程组即可求出x、y的值,即可得答案.
21.【答案】解:设每块地砖的长为xcm,宽为ycm,
根据题意得
解这个方程组,得
45×15×8=5400
【解析】【分析】设每块地砖的长为xcm,宽为ycm,观察图形中拼图可得等量x+y=60.x=3y,据此列出方程组,解出即可.
22.【答案】解:设甲种饮料 瓶,乙种饮料 瓶,
由题意得
解之得
答:生产甲饮料40瓶,乙饮料60瓶
【解析】【分析】本题是二元一次方程组的应用,设甲种饮料 x 瓶,乙种饮料 y 瓶,根据题意列出方程组即可.
23.【答案】解:设甲每分跑x圈,乙每分跑y圈,
根据题意得: ,
解得: .
则甲、乙二人每分各跑 圈与 圈.
【解析】【分析】由题意可知,题中关键的已知条件为:相向而行每隔两分钟相遇一次;同向而行,每隔6分相遇一次,隐含了两个等量关系,然后设未知数,列方程组,然后求出方程组的解。
24.【答案】解:设原有产品m,每个人的包装速度为x,每小时流水线生产的产品为y.
则 ,解得:
若需要n人刚好完成,则2nx=m+y,
∴至少需要18人
【解析】【分析】 设原有产品m,每个人的包装速度为x,每小时流水线生产的产品为y,根据两种方法包装这批产品,总量不变列出方程组,进而即可求出.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
