2021-2022学年浙教版七年级数学下册1.4平行线的性质同步课后作业题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册1.4平行线的性质同步课后作业题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 190.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 10:49:20 | ||
图片预览



文档简介
2021-2022学年浙教版七年级数学下册《1-4平行线的性质》同步课后作业题(附答案)
1.下列说法中正确的有( )个.
①两条直线被第三条直线所截,同位角相等;
②同一平面内,不相交的两条线段一定平行;
③过一点有且只有一条直线垂直于已知直线;
④经过直线外一点有且只有一条直线与这条直线平行;
⑤从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
A.1 B.2 C.3 D.4
2.如图,AB∥DF,AC⊥CE于点C,BC与DF交于点E,若∠A=20°,则∠CED等于( )
A.20° B.50° C.70° D.110°
3.如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( )
A.2α B.90°+α C.180°﹣α D.180°﹣2α
4.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( )
A.25° B.50° C.70° D.77.5°
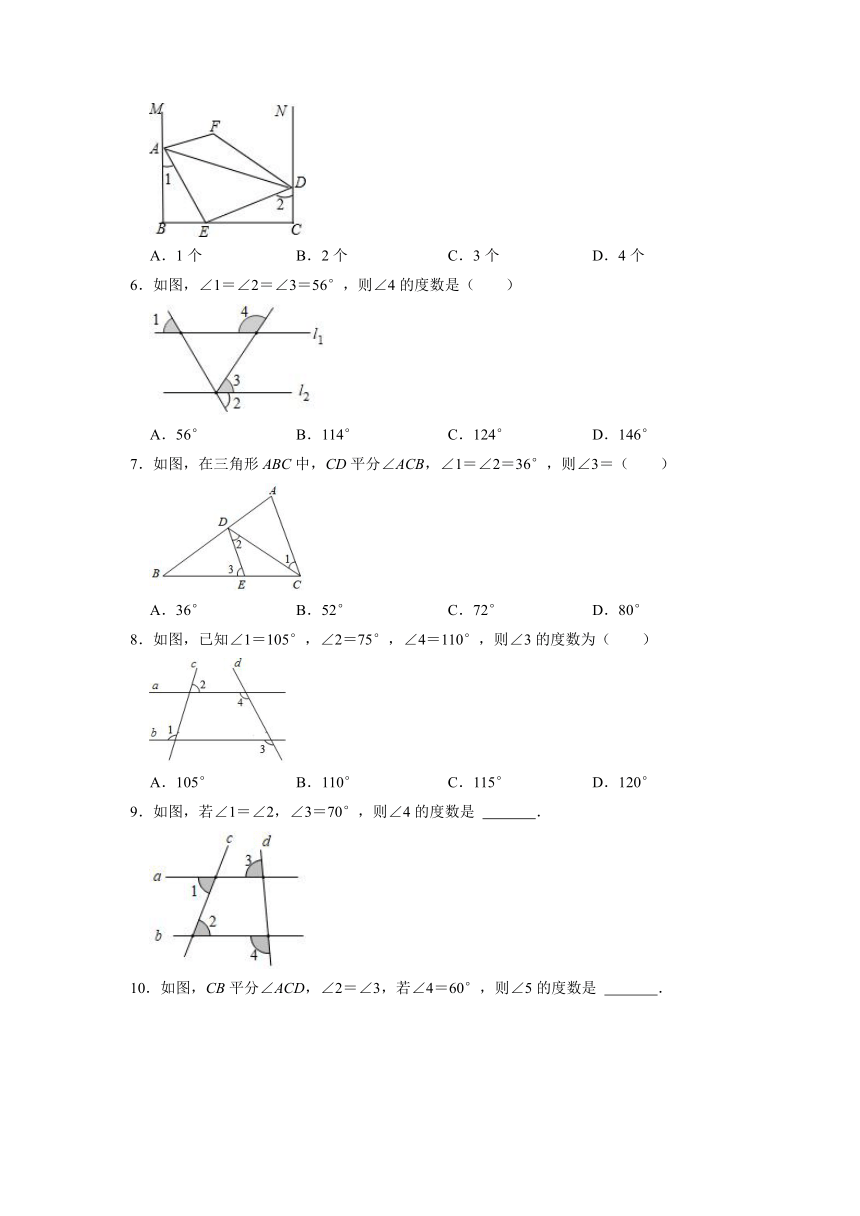
5.如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,∠1=∠2=∠3=56°,则∠4的度数是( )
A.56° B.114° C.124° D.146°
7.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
8.如图,已知∠1=105°,∠2=75°,∠4=110°,则∠3的度数为( )
A.105° B.110° C.115° D.120°
9.如图,若∠1=∠2,∠3=70°,则∠4的度数是 .
10.如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是 .
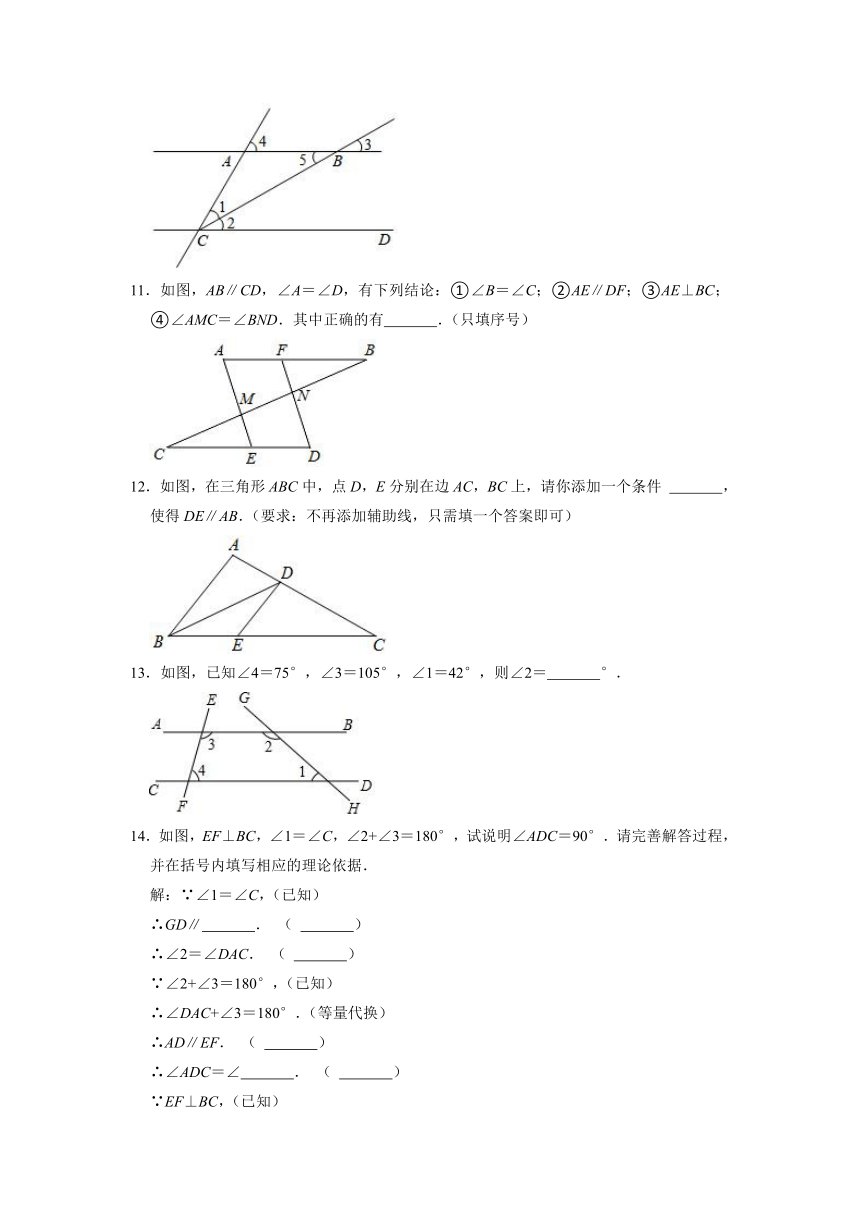
11.如图,AB∥CD,∠A=∠D,有下列结论:①∠B=∠C;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有 .(只填序号)
12.如图,在三角形ABC中,点D,E分别在边AC,BC上,请你添加一个条件 ,使得DE∥AB.(要求:不再添加辅助线,只需填一个答案即可)
13.如图,已知∠4=75°,∠3=105°,∠1=42°,则∠2= °.
14.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ . ( )
∴∠2=∠DAC. ( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. ( )
∴∠ADC=∠ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°. ( )
∴∠ADC=90°.(等量代换)
15.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知),
∠ABC=∠1 ( ),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴( )+∠2=180°(等式的性质),
∴AB∥CD ( ).
又∵∠2+∠BCD=( °),
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D ( ),
∴BC∥DE ( ).
16.如图,∠B=∠BGD,∠BGC=∠F.试说明∠B+∠F=180°.请完善解答过程,并在括号内填写相应的理论根据.
解:∵∠B=∠BGD(已知),
∴ ∥CD( ).
∵∠BGC=∠F(已知),
∴CD∥ ( ).
∴ ∥ (平行于同一直线的两直线平行).
∴∠B+∠F=180°( ).
17.如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠A=∠F,∠C=∠D,求证:∠1=∠2.
18.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
19.完成下面的证明
如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AG∥CD(已知)
∴∠ABC=∠BCD( )
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD( )
∴ =∠BCF(等量代换)
∴BE∥CF( )
∴ =∠F( )
∵BE⊥AF(已知)
∴ =90°( )
∴∠F=90°.
20.如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
21.如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=32°,∠DCE=85°.
(1)求∠DCA的度数;
(2)求∠ACB的度数.
参考答案
1.解:①两条平行线被第三条直线所截,同位角相等,原说法错误;
②同一平面内,不相交的两条线段不一定平行,不相交的两条直线一定平行,原说法错误;
③在同一个平面内,过一点有且只有一条直线垂直于已知直线,原说法错误;
④经过直线外一点有且只有一条直线与这条直线平行,原说法正确;
⑤直线外一点到直线的垂线段的长度,叫做这点到这条直线的距离,原说法错误.
综上所述,说法正确的个数有1个.
故选:A.
2.解:∵AC⊥CE,
∴∠C=90°,
∵∠A=20°,
∴∠ABC=70°,
∵AB∥DF,
∴∠CED=∠ABC=70°.
故选:C.
3.解:由长方形纸带ABCD及折叠性质可得:∠D'EF=∠DEF=α,C'F∥D'E,
∴∠DEG=2∠DEF=2α,∠C'FG=180°﹣∠D'GF,
∵AD∥BC,
∴∠D'GF=∠DEG=2α,
∴∠C'FG=180°﹣2α.
故选:D.
4.解:∵AB∥CD,
∴∠FGB+∠GFD=180°,∠FGB=155°,
∴∠GFD=180°﹣∠FGB=25°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=50°,
∵AB∥CD,
∴∠AEF=∠EFD=50°.
故选:B.
5.解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
综上所述正确的有:①③④,共3个.故选:C.
6.解:如图,
∵∠1=∠2,∠2=∠5,
∴∠1=∠5,
∴l1∥l2,
∴∠3=∠6,
∵∠3=56°,
∴∠6=56°,
∵∠4+∠6=180°,
∴∠4=180°﹣56°=124°,
故选:C.
7.解:∵∠1=∠2=36°,
∴AC∥DE,
∴∠ACB=∠3,
∵CD平分∠ACB,
∴∠ACB=2∠1=72°,
∴∠3=72°.
故选:C.
8.解:∵∠1=105°,
∴∠5=180°﹣∠1=180°﹣105°=75°,
∴∠2=∠5,
∴a∥b,
∵∠4=110°,
∴∠3=∠4=110°,
故选:B.
9.解:如图,
∵∠1=∠2,
∴a∥b,
∴∠5=∠3=70°,
∴∠4=180°﹣∠5=110°.
故答案为:110°.
10.解:∵CB平分∠ACD,
∴∠1=∠2=∠ACD..
∵∠2=∠3,
∴AB∥CD.
∴∠5=∠2,∠4=∠ACD=60°.
∴∠5=∠2=30°.
故答案为:30°.
11.解:∵AB∥CD,
∴∠B=∠C,∠A=∠AEC,
又∵∠A=∠D,
∴∠AEC=∠D,
∴AE∥DF,
∴∠AMC=∠FNM,
又∵∠BND=∠FNM,
∴∠AMC=∠BND,
故①②④正确,
由条件不能得出∠AMC=90°,故③不一定正确;
故答案为:①②④.
12.解:若∠A=∠CDE,
则DE∥AB(同位角相等,两直线平行).(答案不唯一).
故答案为:∠A=∠CDE(答案不唯一).
13.解:∵∠4=75°,∠3=105°,
∴∠4+∠3=75°+105°=180°,
∴AB∥CD,
∴∠1+∠2=180°,
∵∠1=42°,
∴∠2=180°﹣∠2=180°﹣42°=138°,
故答案为:138.
14.解:∵∠1=∠C,(已知)
∴GD∥AC. (同位角相等,两直线平行)
∴∠2=∠DAC. (两直线平行,内错角相等)
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. (同旁内角互补,两直线平行)
∴∠ADC=∠EFC. (两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°. (垂直定义)
∴∠ADC=90°.(等量代换)
故答案为:AC;同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;EFC;两直线平行,同位角相等;垂直定义.
15.解∵∠1=60°(已知),
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行).
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行).
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
16.解:∵∠B=∠BGD(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠BGC=∠F(已知),
∴CD∥EF(同位角相等,两直线平行).
∴AB∥EF(平行于同一直线的两直线平行).
∴∠B+∠F=180°(两直线平行,同旁内角互补).
故答案为:AB;内错角相等,两直线平行;EF;同位角相等,两直线平行;AB;EF;两直线平行,同旁内角互补.
17.证明:∵∠A=∠F,
∴AC∥DF,
∴∠3=∠D;
又∵∠C=∠D,
∴∠C=∠3,
∴BD∥CE,
∴∠1=∠4,
∵∠2=∠4,
∴∠1=∠2.
18.(1)证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
19.证明:∵AG∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵∠ABE=∠FCB(已知),
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB,
即∠EBC=∠FCD,
∵CF平分∠BCD(已知),
∴∠BCF=∠FCD(角平分线的定义),
∴∠EBC=∠BCF(等量代换),
∴BE∥CF(内错角相等,两直线平行),
∴∠BEF=∠F(两直线平行,内错角相等),
∵BE⊥AF(已知),
∴∠BEF=90°(垂直的定义),
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义.
20.证明:∵AE平分∠BAD,
∴∠1=∠2,
∵AD∥BE,
∴∠2=∠E,
∴∠1=∠E,
∵∠CFE=∠E,
∴∠1=∠CFE,
∴AB∥CD.
21.解:(1)∵∠DAB+∠D=180°,
∴DC∥AB,
∴∠DCA=∠CAB,
∵AC平分∠DAB,且∠CAD=32°,
∴∠CAB=∠DCA=32°;
(2)∵∠DCA=32°,∠DCE=85°,
∴∠ACB=180°﹣∠DCE﹣∠DCA=180°﹣32°﹣85°=63°.
1.下列说法中正确的有( )个.
①两条直线被第三条直线所截,同位角相等;
②同一平面内,不相交的两条线段一定平行;
③过一点有且只有一条直线垂直于已知直线;
④经过直线外一点有且只有一条直线与这条直线平行;
⑤从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
A.1 B.2 C.3 D.4
2.如图,AB∥DF,AC⊥CE于点C,BC与DF交于点E,若∠A=20°,则∠CED等于( )
A.20° B.50° C.70° D.110°
3.如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( )
A.2α B.90°+α C.180°﹣α D.180°﹣2α
4.如图,AB∥CD,∠FGB=155°,FG平分∠EFD,则∠AEF的大小为( )
A.25° B.50° C.70° D.77.5°
5.如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,∠1=∠2=∠3=56°,则∠4的度数是( )
A.56° B.114° C.124° D.146°
7.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
8.如图,已知∠1=105°,∠2=75°,∠4=110°,则∠3的度数为( )
A.105° B.110° C.115° D.120°
9.如图,若∠1=∠2,∠3=70°,则∠4的度数是 .
10.如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是 .
11.如图,AB∥CD,∠A=∠D,有下列结论:①∠B=∠C;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.其中正确的有 .(只填序号)
12.如图,在三角形ABC中,点D,E分别在边AC,BC上,请你添加一个条件 ,使得DE∥AB.(要求:不再添加辅助线,只需填一个答案即可)
13.如图,已知∠4=75°,∠3=105°,∠1=42°,则∠2= °.
14.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ . ( )
∴∠2=∠DAC. ( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. ( )
∴∠ADC=∠ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°. ( )
∴∠ADC=90°.(等量代换)
15.如图,如果∠1=60°,∠2=120°,∠D=60°,那么AB与CD平行吗?BC与DE呢?
观察下面的解答过程,补充必要的依据或结论.
解∵∠1=60°(已知),
∠ABC=∠1 ( ),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴( )+∠2=180°(等式的性质),
∴AB∥CD ( ).
又∵∠2+∠BCD=( °),
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D ( ),
∴BC∥DE ( ).
16.如图,∠B=∠BGD,∠BGC=∠F.试说明∠B+∠F=180°.请完善解答过程,并在括号内填写相应的理论根据.
解:∵∠B=∠BGD(已知),
∴ ∥CD( ).
∵∠BGC=∠F(已知),
∴CD∥ ( ).
∴ ∥ (平行于同一直线的两直线平行).
∴∠B+∠F=180°( ).
17.如图,点B,E分别在AC,DF上,BD,CE均与AF相交,∠A=∠F,∠C=∠D,求证:∠1=∠2.
18.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于E.
(1)求证:AD∥BC;
(2)若∠ADB=36°,求∠EFC的度数.
19.完成下面的证明
如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AG∥CD(已知)
∴∠ABC=∠BCD( )
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD( )
∴ =∠BCF(等量代换)
∴BE∥CF( )
∴ =∠F( )
∵BE⊥AF(已知)
∴ =90°( )
∴∠F=90°.
20.如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
21.如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=32°,∠DCE=85°.
(1)求∠DCA的度数;
(2)求∠ACB的度数.
参考答案
1.解:①两条平行线被第三条直线所截,同位角相等,原说法错误;
②同一平面内,不相交的两条线段不一定平行,不相交的两条直线一定平行,原说法错误;
③在同一个平面内,过一点有且只有一条直线垂直于已知直线,原说法错误;
④经过直线外一点有且只有一条直线与这条直线平行,原说法正确;
⑤直线外一点到直线的垂线段的长度,叫做这点到这条直线的距离,原说法错误.
综上所述,说法正确的个数有1个.
故选:A.
2.解:∵AC⊥CE,
∴∠C=90°,
∵∠A=20°,
∴∠ABC=70°,
∵AB∥DF,
∴∠CED=∠ABC=70°.
故选:C.
3.解:由长方形纸带ABCD及折叠性质可得:∠D'EF=∠DEF=α,C'F∥D'E,
∴∠DEG=2∠DEF=2α,∠C'FG=180°﹣∠D'GF,
∵AD∥BC,
∴∠D'GF=∠DEG=2α,
∴∠C'FG=180°﹣2α.
故选:D.
4.解:∵AB∥CD,
∴∠FGB+∠GFD=180°,∠FGB=155°,
∴∠GFD=180°﹣∠FGB=25°,
∵FG平分∠EFD,
∴∠EFD=2∠GFD=50°,
∵AB∥CD,
∴∠AEF=∠EFD=50°.
故选:B.
5.解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
综上所述正确的有:①③④,共3个.故选:C.
6.解:如图,
∵∠1=∠2,∠2=∠5,
∴∠1=∠5,
∴l1∥l2,
∴∠3=∠6,
∵∠3=56°,
∴∠6=56°,
∵∠4+∠6=180°,
∴∠4=180°﹣56°=124°,
故选:C.
7.解:∵∠1=∠2=36°,
∴AC∥DE,
∴∠ACB=∠3,
∵CD平分∠ACB,
∴∠ACB=2∠1=72°,
∴∠3=72°.
故选:C.
8.解:∵∠1=105°,
∴∠5=180°﹣∠1=180°﹣105°=75°,
∴∠2=∠5,
∴a∥b,
∵∠4=110°,
∴∠3=∠4=110°,
故选:B.
9.解:如图,
∵∠1=∠2,
∴a∥b,
∴∠5=∠3=70°,
∴∠4=180°﹣∠5=110°.
故答案为:110°.
10.解:∵CB平分∠ACD,
∴∠1=∠2=∠ACD..
∵∠2=∠3,
∴AB∥CD.
∴∠5=∠2,∠4=∠ACD=60°.
∴∠5=∠2=30°.
故答案为:30°.
11.解:∵AB∥CD,
∴∠B=∠C,∠A=∠AEC,
又∵∠A=∠D,
∴∠AEC=∠D,
∴AE∥DF,
∴∠AMC=∠FNM,
又∵∠BND=∠FNM,
∴∠AMC=∠BND,
故①②④正确,
由条件不能得出∠AMC=90°,故③不一定正确;
故答案为:①②④.
12.解:若∠A=∠CDE,
则DE∥AB(同位角相等,两直线平行).(答案不唯一).
故答案为:∠A=∠CDE(答案不唯一).
13.解:∵∠4=75°,∠3=105°,
∴∠4+∠3=75°+105°=180°,
∴AB∥CD,
∴∠1+∠2=180°,
∵∠1=42°,
∴∠2=180°﹣∠2=180°﹣42°=138°,
故答案为:138.
14.解:∵∠1=∠C,(已知)
∴GD∥AC. (同位角相等,两直线平行)
∴∠2=∠DAC. (两直线平行,内错角相等)
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF. (同旁内角互补,两直线平行)
∴∠ADC=∠EFC. (两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°. (垂直定义)
∴∠ADC=90°.(等量代换)
故答案为:AC;同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;EFC;两直线平行,同位角相等;垂直定义.
15.解∵∠1=60°(已知),
∠ABC=∠1 (对顶角相等),
∴∠ABC=60°(等量代换).
又∵∠2=120°(已知),
∴∠ABC+∠2=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行).
又∵∠2+∠BCD=180°,
∴∠BCD=60°(等式的性质).
∵∠D=60°(已知),
∴∠BCD=∠D (等量代换),
∴BC∥DE (内错角相等,两直线平行).
故答案为:对顶角相等;∠ABC;同旁内角互补,两直线平行;180;等量代换;内错角相等,两直线平行.
16.解:∵∠B=∠BGD(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠BGC=∠F(已知),
∴CD∥EF(同位角相等,两直线平行).
∴AB∥EF(平行于同一直线的两直线平行).
∴∠B+∠F=180°(两直线平行,同旁内角互补).
故答案为:AB;内错角相等,两直线平行;EF;同位角相等,两直线平行;AB;EF;两直线平行,同旁内角互补.
17.证明:∵∠A=∠F,
∴AC∥DF,
∴∠3=∠D;
又∵∠C=∠D,
∴∠C=∠3,
∴BD∥CE,
∴∠1=∠4,
∵∠2=∠4,
∴∠1=∠2.
18.(1)证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)∵AD∥BC,∠ADB=36°,
∴∠DBC=∠ADB=36°,
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠DBC=∠EFC=36°
19.证明:∵AG∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等),
∵∠ABE=∠FCB(已知),
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB,
即∠EBC=∠FCD,
∵CF平分∠BCD(已知),
∴∠BCF=∠FCD(角平分线的定义),
∴∠EBC=∠BCF(等量代换),
∴BE∥CF(内错角相等,两直线平行),
∴∠BEF=∠F(两直线平行,内错角相等),
∵BE⊥AF(已知),
∴∠BEF=90°(垂直的定义),
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠EBC;内错角相等,两直线平行;∠BEF;两直线平行,内错角相等;∠BEF;垂直的定义.
20.证明:∵AE平分∠BAD,
∴∠1=∠2,
∵AD∥BE,
∴∠2=∠E,
∴∠1=∠E,
∵∠CFE=∠E,
∴∠1=∠CFE,
∴AB∥CD.
21.解:(1)∵∠DAB+∠D=180°,
∴DC∥AB,
∴∠DCA=∠CAB,
∵AC平分∠DAB,且∠CAD=32°,
∴∠CAB=∠DCA=32°;
(2)∵∠DCA=32°,∠DCE=85°,
∴∠ACB=180°﹣∠DCE﹣∠DCA=180°﹣32°﹣85°=63°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
