2021-2022学年浙教版七年级数学下册 1.3平行线的判定 同步课后作业题(word版含解析)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册 1.3平行线的判定 同步课后作业题(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览


文档简介
2021-2022学年浙教版七年级数学下册《1-3平行线的判定》同步课后作业题(附答案)
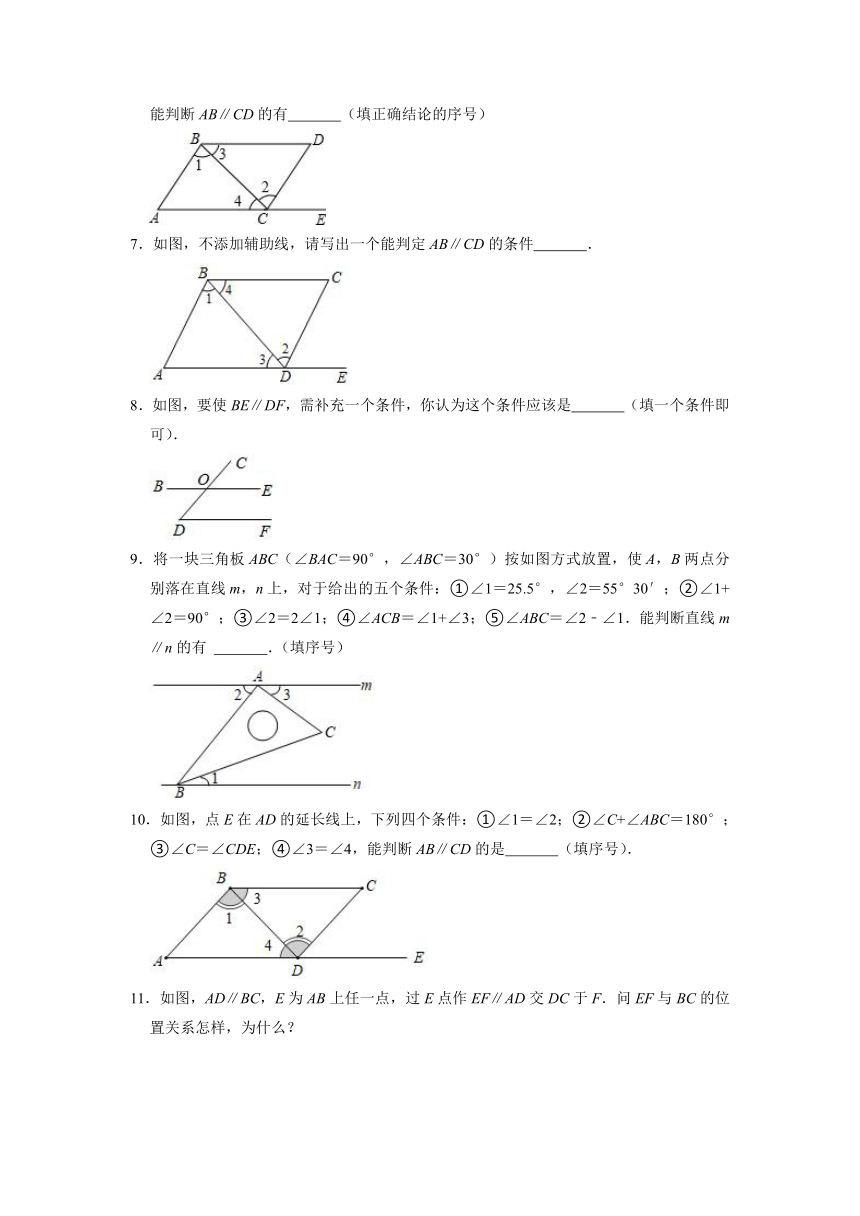
1.如图,下列说法错误的是( )
A.∵∠1=∠2,∴l3∥l4 B.∵∠2+∠5=180°,∴l3∥l4
C.∵∠1=∠4,∴l1∥l2 D.∵∠1=∠3,∴l1∥l2
2.如图,下列四个选项中不能判断AD∥BC的是( )
A.∠1=∠3 B.∠B+∠BAD=180°
C.∠D=∠5 D.∠2=∠4
3.直线AB、BC、CD、EG如图所示.若∠1=∠2,则下列结论错误的是( )
A.AB∥CD B.∠EFB=∠3 C.∠4=∠5 D.∠3=∠5
4.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A. B.
C. D.
5.如图,下列条件中,不能判断直线a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
6.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有 (填正确结论的序号)
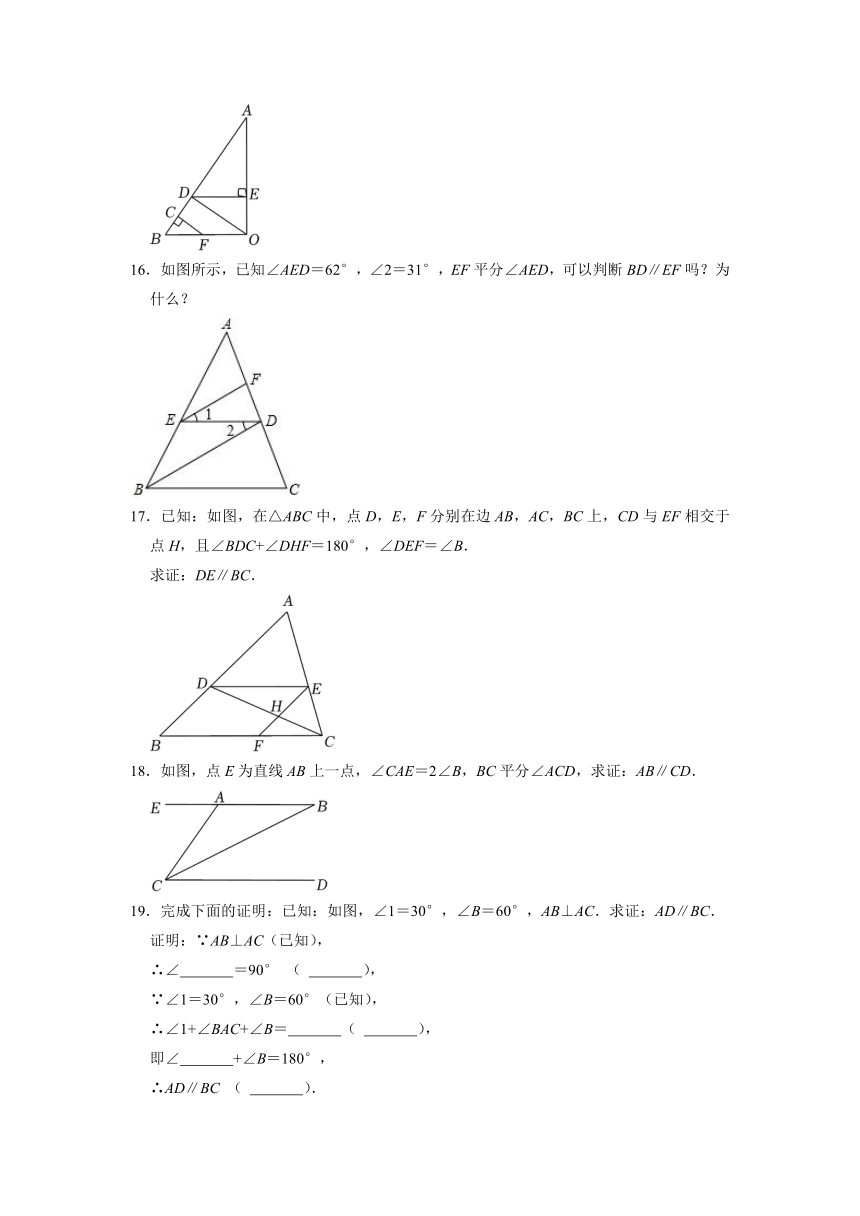
7.如图,不添加辅助线,请写出一个能判定AB∥CD的条件 .
8.如图,要使BE∥DF,需补充一个条件,你认为这个条件应该是 (填一个条件即可).
9.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上,对于给出的五个条件:①∠1=25.5°,∠2=55°30′;②∠1+∠2=90°;③∠2=2∠1;④∠ACB=∠1+∠3;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
10.如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是 (填序号).
11.如图,AD∥BC,E为AB上任一点,过E点作EF∥AD交DC于F.问EF与BC的位置关系怎样,为什么?
12.如图,如果CD∥AB,CE∥AB,那么C,D,E三点是否共线?你能说明理由吗?
13.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
14.已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数;请补全下列解法中的空缺部分.
解:过点P作PG∥AB交AC于点G.
∵AB∥CD( ),
∴ +∠ACD=180°( ),
∵PG∥AB( ),
∴∠BAP= ( ),
且PG∥ (平行于同一直线的两直线也互相平行),
∴∠GPC= (两直线平行,内错角相等),
∵AP平分∠BAC,CP平分∠ACD.
∴∠BAP=∠ ,∠PCD=∠ .( ),
∴∠BAP+∠PCD=∠BAC+∠ACD=90°( ),
∴∠APC=∠APG+∠CPG=∠BAP+∠CDP=90°.
总结:两直线平行时,同旁内角的角平分线 .
15.如图,△ABO中,∠AOB=90°,DE⊥AO于点E,∠CFB=∠EDO.
证明:CF∥DO.
如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判断BD∥EF吗?为什么?
17.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.
求证:DE∥BC.
18.如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
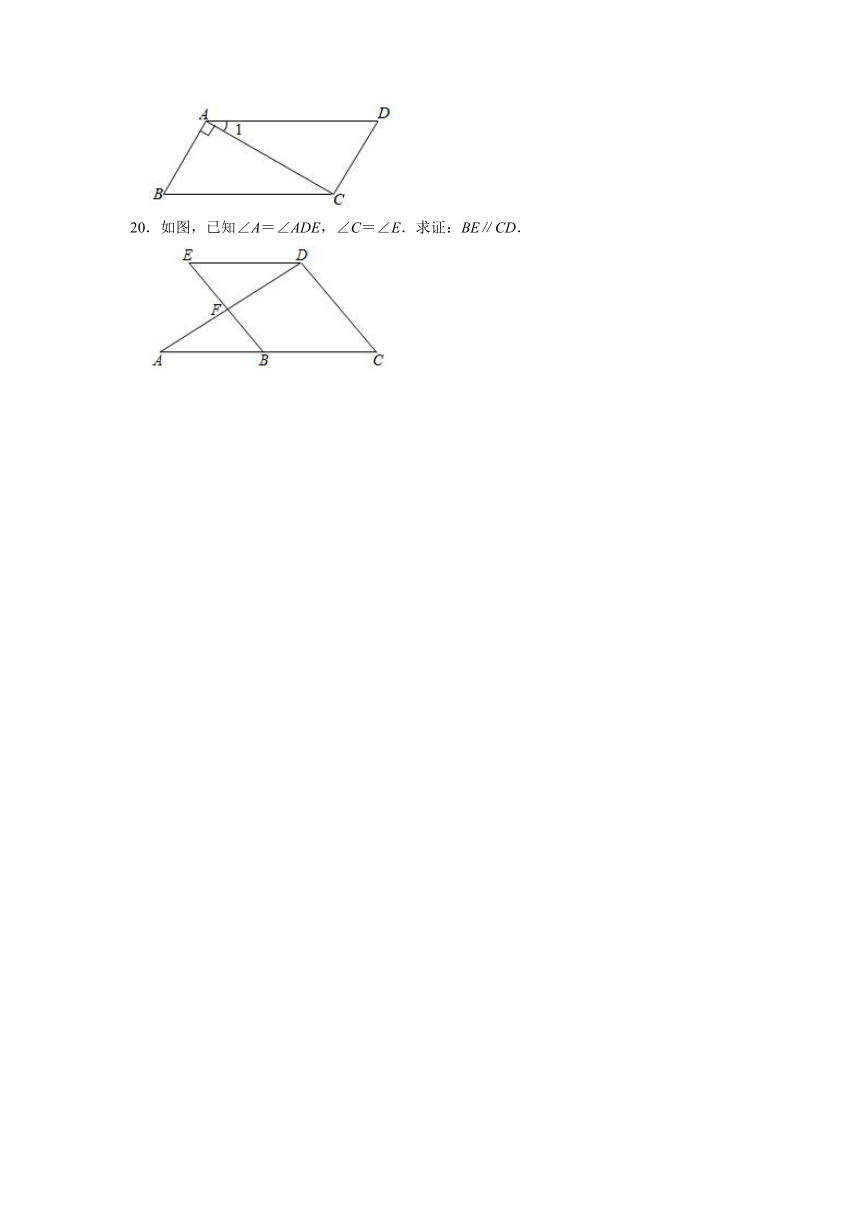
19.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知),
∴∠ =90° ( ),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B= ( ),
即∠ +∠B=180°,
∴AD∥BC ( ).
20.如图,已知∠A=∠ADE,∠C=∠E.求证:BE∥CD.
参考答案
1.解:A、∵∠1=∠2,∴l3∥l4(内错角相等,两直线平行),不符合题意;
B、∵∠2+∠5=180°,∴l3∥l4(同旁内角互补,两直线平行),不符合题意;
C、∵∠1=∠4,∴l1∥l2(内错角相等,两直线平行),不符合题意;
D、由∠1=∠3不能得到l1∥l2,符合题意.
故选:D.
2.解:A、∵∠1=∠3,
∴AD∥BC,故此选项不符合题意;
B、∵∠B+∠BAD=180°,
∴AD∥BC,故此选项不符合题意;
C、∵∠D=∠5,
∴AD∥BC,故此选项不符合题意;
D、∵∠2=∠4,
∴AB∥CD,故此选项符合题意;
故选:D.
3.解:∵∠1=∠2,
∴AB∥CD,
故A正确,不符合题意;
∠EFB=∠3,
故B正确,不符合题意;
∵AB∥CD,
∴∠4=∠5,
故C正确,不符合题意;
无法得到∠3=∠5,
故D错误,符合题意.
故选:D.
4.解:第一个图中,∠1、∠2不是两条直线被第三条直线所截的内错角或同位角,不能判定AB∥CD;
第二个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第三个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第四个图中,∠1、∠2是两条直线被第三条直线所截的同位角,能判定AB∥CD;
故选:D.
5.解:当∠1=∠3时,a∥b;
当∠4=∠5时,a∥b;
当∠2+∠4=180°时,a∥b.
故选:B.
6.解:①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故答案为②③④.
7.解:添加∠1=∠2,
∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行),
故答案为:∠1=∠2(答案不唯一).
8.解:添加条件为:∠D=∠COE.
理由如下:
∵∠D=∠COE,
∴BE∥DF(同位角相等,两直线平行).
故答案为:∠D=∠COE(答案不唯一).
9.解:∵∠1=25.5°,∠2=55°30′,∠ABC=30°,
∴∠ABC+∠1=55.5°=55°30′=∠2,
∴m∥n,故①符合题意;
∵∠1+∠2=90°,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故②不符合题意;
∵∠2=2∠1,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故③不符合题意;
过点C作CE∥m,
∴∠3=∠4,
∵∠ACB=∠1+∠3,∠ACB=∠4+∠5,
∴∠1=∠5,
∴EC∥n,
∴m∥n,故④符合题意;
∵∠ABC=∠2﹣∠1,
∴∠2=∠ABC+∠1,
∴m∥n,故⑤符合题意;
故答案为:①④⑤.
10.解:①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
11.解:∵AD∥BC,EF∥AD,
∴EF∥BC(平行公理).
12.解:共线.
因为过直线AB外一点C有且只有一条直线与AB平行,CD、DE都经过点C且与AB平行,
所以点C、D、E三点共线.
13.解:∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
14.解:过点P作PG∥AB交AC于点G.
∵AB∥CD(已知),
∴∠CAB+∠ACD=180°(两直线平行,同旁内角互补),
∵PG∥AB(已知),
∴∠BAP=∠APG(两直线平行,内错角相等),
且PG∥CD(平行于同一直线的两直线也互相平行),
∴∠GPC=∠PCD(两直线平行,内错角相等),
∵AP平分∠BAC,CP平分∠ACD,
∴,(角平分线定义),
∴(等量代换),
∴∠APC=∠APG+∠CPG=∠BAP+∠CDP=90°.
总结:两直线平行时,同旁内角的角平分线互相垂直.
故答案为:已知;∠CAB;两直线平行,同旁内角互补;CD;∠PCD;BAC;ACD;角平分线定义;等量代换;互相垂直.
15.证明:∵DE⊥AO,
∴∠AED=90°,
∴∠AED=∠AOB=90°,
∴DE∥BO,
∴∠EDO=∠BOD,
∵∠EDO=∠CFB,
∴∠BOD=∠CFB,
∴CF∥DO.
16.解:BD∥EF;理由如下:
∵∠AED=62°,EF平分∠AED,
∴∠1=∠AED=31°,
∵∠2=31°,
∴∠1=∠2,
∴BD∥EF.
17.证明:∵∠BDC+∠DHF=180°,
∴BD∥FH,
∴∠B=∠EFC,
∵∠DEF=∠B,
∴∠EFC=∠DEF,
∴DE∥BC.
18.证明:由题意知∠CAE=∠ACB+∠B(三角形外角的性质),
∵∠CAE=2∠B(已知),
∴∠B=∠ACB(等量代换),
又∵BC平分∠ACD(已知),
∴∠ACB=∠DCB(角平分线的定义),
∴∠B=∠DCB(等量代换),
∴AB∥CD(内错角相等,两直线平行).
19.解:证明:∵AB⊥AC(已知),
∴∠BAC=90° (垂直的定义),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B=180°(等量关系),
即∠BAD+∠B=180°,
∴AD∥BC (同旁内角互补,两直线平行),
故答案为:BAC;垂直的定义;180°;等量关系;BAD;同旁内角互补,两直线平行.
20.证明:∵∠A=∠ADE,
∴DE∥AC,
∴∠ABE=∠E,
又∵∠C=∠E,
∴∠ABE=∠C,
∴BE∥CD.
1.如图,下列说法错误的是( )
A.∵∠1=∠2,∴l3∥l4 B.∵∠2+∠5=180°,∴l3∥l4
C.∵∠1=∠4,∴l1∥l2 D.∵∠1=∠3,∴l1∥l2
2.如图,下列四个选项中不能判断AD∥BC的是( )
A.∠1=∠3 B.∠B+∠BAD=180°
C.∠D=∠5 D.∠2=∠4
3.直线AB、BC、CD、EG如图所示.若∠1=∠2,则下列结论错误的是( )
A.AB∥CD B.∠EFB=∠3 C.∠4=∠5 D.∠3=∠5
4.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A. B.
C. D.
5.如图,下列条件中,不能判断直线a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
6.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有 (填正确结论的序号)
7.如图,不添加辅助线,请写出一个能判定AB∥CD的条件 .
8.如图,要使BE∥DF,需补充一个条件,你认为这个条件应该是 (填一个条件即可).
9.将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,n上,对于给出的五个条件:①∠1=25.5°,∠2=55°30′;②∠1+∠2=90°;③∠2=2∠1;④∠ACB=∠1+∠3;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
10.如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是 (填序号).
11.如图,AD∥BC,E为AB上任一点,过E点作EF∥AD交DC于F.问EF与BC的位置关系怎样,为什么?
12.如图,如果CD∥AB,CE∥AB,那么C,D,E三点是否共线?你能说明理由吗?
13.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
14.已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数;请补全下列解法中的空缺部分.
解:过点P作PG∥AB交AC于点G.
∵AB∥CD( ),
∴ +∠ACD=180°( ),
∵PG∥AB( ),
∴∠BAP= ( ),
且PG∥ (平行于同一直线的两直线也互相平行),
∴∠GPC= (两直线平行,内错角相等),
∵AP平分∠BAC,CP平分∠ACD.
∴∠BAP=∠ ,∠PCD=∠ .( ),
∴∠BAP+∠PCD=∠BAC+∠ACD=90°( ),
∴∠APC=∠APG+∠CPG=∠BAP+∠CDP=90°.
总结:两直线平行时,同旁内角的角平分线 .
15.如图,△ABO中,∠AOB=90°,DE⊥AO于点E,∠CFB=∠EDO.
证明:CF∥DO.
如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判断BD∥EF吗?为什么?
17.已知:如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°,∠DEF=∠B.
求证:DE∥BC.
18.如图,点E为直线AB上一点,∠CAE=2∠B,BC平分∠ACD,求证:AB∥CD.
19.完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.
证明:∵AB⊥AC(已知),
∴∠ =90° ( ),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B= ( ),
即∠ +∠B=180°,
∴AD∥BC ( ).
20.如图,已知∠A=∠ADE,∠C=∠E.求证:BE∥CD.
参考答案
1.解:A、∵∠1=∠2,∴l3∥l4(内错角相等,两直线平行),不符合题意;
B、∵∠2+∠5=180°,∴l3∥l4(同旁内角互补,两直线平行),不符合题意;
C、∵∠1=∠4,∴l1∥l2(内错角相等,两直线平行),不符合题意;
D、由∠1=∠3不能得到l1∥l2,符合题意.
故选:D.
2.解:A、∵∠1=∠3,
∴AD∥BC,故此选项不符合题意;
B、∵∠B+∠BAD=180°,
∴AD∥BC,故此选项不符合题意;
C、∵∠D=∠5,
∴AD∥BC,故此选项不符合题意;
D、∵∠2=∠4,
∴AB∥CD,故此选项符合题意;
故选:D.
3.解:∵∠1=∠2,
∴AB∥CD,
故A正确,不符合题意;
∠EFB=∠3,
故B正确,不符合题意;
∵AB∥CD,
∴∠4=∠5,
故C正确,不符合题意;
无法得到∠3=∠5,
故D错误,符合题意.
故选:D.
4.解:第一个图中,∠1、∠2不是两条直线被第三条直线所截的内错角或同位角,不能判定AB∥CD;
第二个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第三个图中,∠1、∠2不是两条直线被第三条直线所截的同位角,不能判定AB∥CD;
第四个图中,∠1、∠2是两条直线被第三条直线所截的同位角,能判定AB∥CD;
故选:D.
5.解:当∠1=∠3时,a∥b;
当∠4=∠5时,a∥b;
当∠2+∠4=180°时,a∥b.
故选:B.
6.解:①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故答案为②③④.
7.解:添加∠1=∠2,
∵∠1=∠2,
∴AB∥CD(内错角相等,两直线平行),
故答案为:∠1=∠2(答案不唯一).
8.解:添加条件为:∠D=∠COE.
理由如下:
∵∠D=∠COE,
∴BE∥DF(同位角相等,两直线平行).
故答案为:∠D=∠COE(答案不唯一).
9.解:∵∠1=25.5°,∠2=55°30′,∠ABC=30°,
∴∠ABC+∠1=55.5°=55°30′=∠2,
∴m∥n,故①符合题意;
∵∠1+∠2=90°,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故②不符合题意;
∵∠2=2∠1,∠ABC=30°,
∴∠1+∠ABC不一定等于∠2,
∴m和n不一定平行,故③不符合题意;
过点C作CE∥m,
∴∠3=∠4,
∵∠ACB=∠1+∠3,∠ACB=∠4+∠5,
∴∠1=∠5,
∴EC∥n,
∴m∥n,故④符合题意;
∵∠ABC=∠2﹣∠1,
∴∠2=∠ABC+∠1,
∴m∥n,故⑤符合题意;
故答案为:①④⑤.
10.解:①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
11.解:∵AD∥BC,EF∥AD,
∴EF∥BC(平行公理).
12.解:共线.
因为过直线AB外一点C有且只有一条直线与AB平行,CD、DE都经过点C且与AB平行,
所以点C、D、E三点共线.
13.解:∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
14.解:过点P作PG∥AB交AC于点G.
∵AB∥CD(已知),
∴∠CAB+∠ACD=180°(两直线平行,同旁内角互补),
∵PG∥AB(已知),
∴∠BAP=∠APG(两直线平行,内错角相等),
且PG∥CD(平行于同一直线的两直线也互相平行),
∴∠GPC=∠PCD(两直线平行,内错角相等),
∵AP平分∠BAC,CP平分∠ACD,
∴,(角平分线定义),
∴(等量代换),
∴∠APC=∠APG+∠CPG=∠BAP+∠CDP=90°.
总结:两直线平行时,同旁内角的角平分线互相垂直.
故答案为:已知;∠CAB;两直线平行,同旁内角互补;CD;∠PCD;BAC;ACD;角平分线定义;等量代换;互相垂直.
15.证明:∵DE⊥AO,
∴∠AED=90°,
∴∠AED=∠AOB=90°,
∴DE∥BO,
∴∠EDO=∠BOD,
∵∠EDO=∠CFB,
∴∠BOD=∠CFB,
∴CF∥DO.
16.解:BD∥EF;理由如下:
∵∠AED=62°,EF平分∠AED,
∴∠1=∠AED=31°,
∵∠2=31°,
∴∠1=∠2,
∴BD∥EF.
17.证明:∵∠BDC+∠DHF=180°,
∴BD∥FH,
∴∠B=∠EFC,
∵∠DEF=∠B,
∴∠EFC=∠DEF,
∴DE∥BC.
18.证明:由题意知∠CAE=∠ACB+∠B(三角形外角的性质),
∵∠CAE=2∠B(已知),
∴∠B=∠ACB(等量代换),
又∵BC平分∠ACD(已知),
∴∠ACB=∠DCB(角平分线的定义),
∴∠B=∠DCB(等量代换),
∴AB∥CD(内错角相等,两直线平行).
19.解:证明:∵AB⊥AC(已知),
∴∠BAC=90° (垂直的定义),
∵∠1=30°,∠B=60°(已知),
∴∠1+∠BAC+∠B=180°(等量关系),
即∠BAD+∠B=180°,
∴AD∥BC (同旁内角互补,两直线平行),
故答案为:BAC;垂直的定义;180°;等量关系;BAD;同旁内角互补,两直线平行.
20.证明:∵∠A=∠ADE,
∴DE∥AC,
∴∠ABE=∠E,
又∵∠C=∠E,
∴∠ABE=∠C,
∴BE∥CD.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
