2021-2022学年浙教版七年级数学下册1.3.1平行线的判定 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册1.3.1平行线的判定 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 613.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-24 13:25:12 | ||
图片预览





文档简介
(共15张PPT)
1.3 平行线的判定
辨别、断定之意
知识点-复行线的定义:
在同一平面内,永不相交的两条直线叫做平行线.
知识点
试判断直线AB是否平行于CD?
根据定义在同一平面内,永不相交的两条直线叫做平行线.
根据定义法判定 优点:可以用于所有情况,只要符合定义的两条直线必平行
缺点:无法直观的确认
那是否还有其他的方法判断两直线是否平行?
知识点
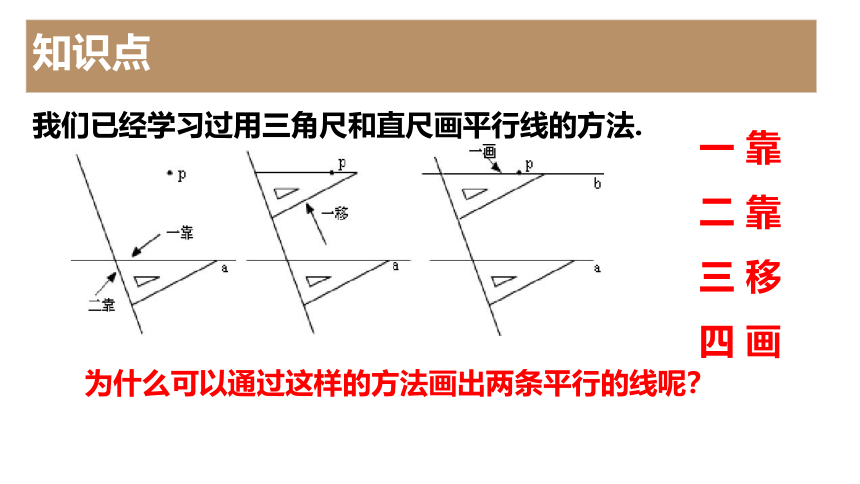
我们已经学习过用三角尺和直尺画平行线的方法.
一 靠
二 靠
三 移
四 画
为什么可以通过这样的方法画出两条平行的线呢?
讨论
把图中的直线PB,DE看成被尺边AC所截,那么在画图过程中,什么角始终保持相等?
P
B
A
C
D
E
同位角
由此你能发现判定两直线平行的方法吗
知识点
人们在长期实践中总结出以下基本事实:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法1
几何语言:
∵∠1=∠2
∴AB∥CD(同位角相等,两直线平行)
练一练
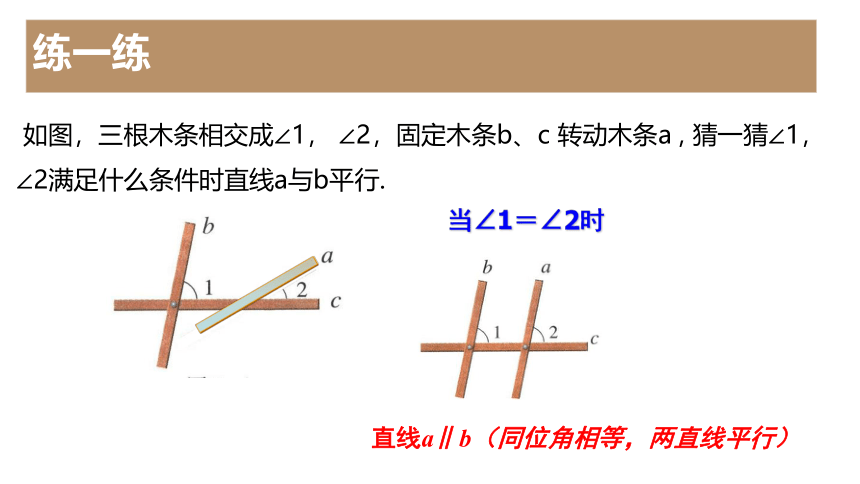
如图,三根木条相交成∠1, ∠2,固定木条b、c 转动木条a , 猜一猜∠1, ∠2满足什么条件时直线a与b平行.
当∠1=∠2时
直线a∥b(同位角相等,两直线平行)
练一练
如图,哪两个角相等能判定直线AB∥CD
1
4
3
2
A
D
C
B
∠3=∠4(同位角相等,两直线平行)
例题
例1、已知直线l1,l2被l3所截, 1=45 , 2=135 ,判断l1 与 l2 是否平行,并说明理由。
l1
l2
l3
解: l1∥ l2.理由如下:
由已知,得∠2+∠3=180°
∴∠3=180°-∠2=180° -135° =45°
又∵∠1=45°
∴∠1=∠3=45°
∴ l1∥ l2(同位角相等,两直线平行)
例题
如图,AB⊥EF,CD⊥EF,E、F分别为垂足. 直线AB与CD平行吗?请说明理由.
解:AB∥CD.理由如下:
∵ AB⊥EF,CD ⊥ EF,
根据垂直的意义,得∠1=∠2=Rt∠
∴ AB∥CD(同位角相等,两直线平行)
推论:“在同一平面 ,垂直于同一条直线的两条直线互相平行”.
练一练
1、(1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD.
57
(2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系?
a∥b
练一练
2.如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.内错角相等,两直线平行
D.两直线平行,内错角相等
A
练一练
3.如图,在四边形ABCD中,∠B=∠D= 90 ,AE、CF分别平分∠BAD和∠BCD.求证:AE∥CF.
解:根据图形可知:
∵ABCD是四边形
∴∠BAD+∠B+∠BCD+∠D= 360 (四边形的内角和为360°)
∵∠B=∠D= 90 (已知)
∴∠BAD+∠BCD= 180
∵AE平分∠BAD,CF平分∠BCD
∴∠BAE= 1/2 ∠BAD,∠BCF= 1/2 ∠BCD(角平分线的性质)
∴∠BAE+∠BCF= 90
∵∠BFC+∠BCF= 90
∴∠BFC=∠BAE(同角的余角相同)
∴AE∥CF
练一练
4、某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图)。这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由.
本课小节
两直线平行线的判定方法:
1、定义:
在同一平面内,不相交的两条直线叫平行线。
2、平行线判定公理:
两条直线被第三条直线所截,如果同位角相等,那么两直线平行
3、平行线判定公理推论:
在同一平面 ,垂直于同一条直线的两条直线互相平行
1.3 平行线的判定
辨别、断定之意
知识点-复行线的定义:
在同一平面内,永不相交的两条直线叫做平行线.
知识点
试判断直线AB是否平行于CD?
根据定义在同一平面内,永不相交的两条直线叫做平行线.
根据定义法判定 优点:可以用于所有情况,只要符合定义的两条直线必平行
缺点:无法直观的确认
那是否还有其他的方法判断两直线是否平行?
知识点
我们已经学习过用三角尺和直尺画平行线的方法.
一 靠
二 靠
三 移
四 画
为什么可以通过这样的方法画出两条平行的线呢?
讨论
把图中的直线PB,DE看成被尺边AC所截,那么在画图过程中,什么角始终保持相等?
P
B
A
C
D
E
同位角
由此你能发现判定两直线平行的方法吗
知识点
人们在长期实践中总结出以下基本事实:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法1
几何语言:
∵∠1=∠2
∴AB∥CD(同位角相等,两直线平行)
练一练
如图,三根木条相交成∠1, ∠2,固定木条b、c 转动木条a , 猜一猜∠1, ∠2满足什么条件时直线a与b平行.
当∠1=∠2时
直线a∥b(同位角相等,两直线平行)
练一练
如图,哪两个角相等能判定直线AB∥CD
1
4
3
2
A
D
C
B
∠3=∠4(同位角相等,两直线平行)
例题
例1、已知直线l1,l2被l3所截, 1=45 , 2=135 ,判断l1 与 l2 是否平行,并说明理由。
l1
l2
l3
解: l1∥ l2.理由如下:
由已知,得∠2+∠3=180°
∴∠3=180°-∠2=180° -135° =45°
又∵∠1=45°
∴∠1=∠3=45°
∴ l1∥ l2(同位角相等,两直线平行)
例题
如图,AB⊥EF,CD⊥EF,E、F分别为垂足. 直线AB与CD平行吗?请说明理由.
解:AB∥CD.理由如下:
∵ AB⊥EF,CD ⊥ EF,
根据垂直的意义,得∠1=∠2=Rt∠
∴ AB∥CD(同位角相等,两直线平行)
推论:“在同一平面 ,垂直于同一条直线的两条直线互相平行”.
练一练
1、(1)如图1,∠C=57°,
当∠ABE= °时,就能使BE∥CD.
57
(2)如图2 , ∠1=120°,∠2=60°.
问a与b的关系?
a∥b
练一练
2.如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是( )
A.同位角相等,两直线平行
B.两直线平行,同位角相等
C.内错角相等,两直线平行
D.两直线平行,内错角相等
A
练一练
3.如图,在四边形ABCD中,∠B=∠D= 90 ,AE、CF分别平分∠BAD和∠BCD.求证:AE∥CF.
解:根据图形可知:
∵ABCD是四边形
∴∠BAD+∠B+∠BCD+∠D= 360 (四边形的内角和为360°)
∵∠B=∠D= 90 (已知)
∴∠BAD+∠BCD= 180
∵AE平分∠BAD,CF平分∠BCD
∴∠BAE= 1/2 ∠BAD,∠BCF= 1/2 ∠BCD(角平分线的性质)
∴∠BAE+∠BCF= 90
∵∠BFC+∠BCF= 90
∴∠BFC=∠BAE(同角的余角相同)
∴AE∥CF
练一练
4、某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图)。这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由.
本课小节
两直线平行线的判定方法:
1、定义:
在同一平面内,不相交的两条直线叫平行线。
2、平行线判定公理:
两条直线被第三条直线所截,如果同位角相等,那么两直线平行
3、平行线判定公理推论:
在同一平面 ,垂直于同一条直线的两条直线互相平行
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
