2021-2022学年浙教版七年级数学下册1.4平行线的性质同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册1.4平行线的性质同步达标测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 285.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 20:00:59 | ||
图片预览


文档简介
2021-2022学年浙教版七年级数学下册《1-4平行线的性质》同步达标测试题(附答案)
一.选择题(共7小题,满分35分)
1.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,B分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
2.如图,已知∠1=65°,如果CD∥BE,那么∠B的度数为( )
A.65° B.105° C.115° D.125°
3.如图,直线EF分别交AB、CD于点E、F,EG平分∠BEF,AB∥CD.若∠1=72°,则∠2的度数为( )
A.54° B.59° C.72° D.108°
4.如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
A.22° B.28° C.32° D.38°
5.如图,在平面内,把矩形ABCD沿EF对折,若∠1=40°,则∠AEF等于( )
A.115° B.110° C.120° D.65°
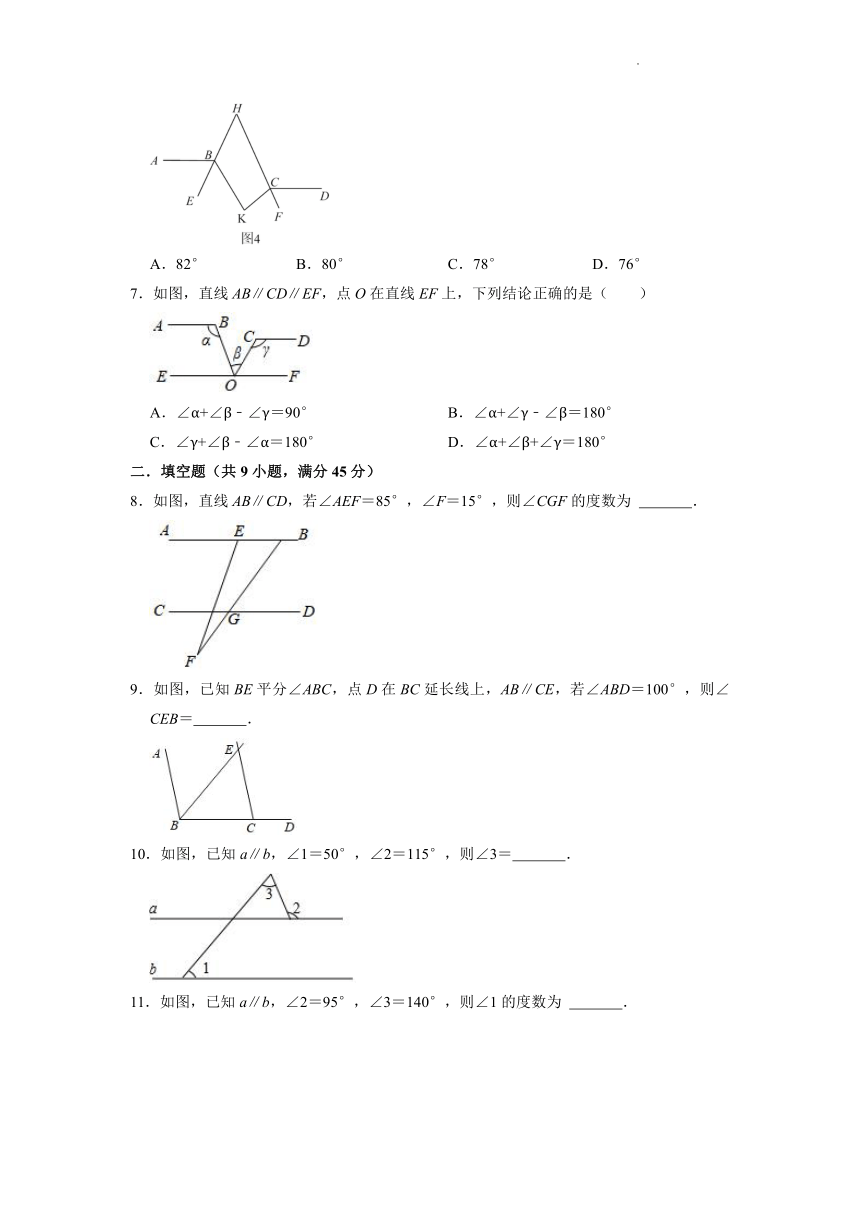
6.如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A.82° B.80° C.78° D.76°
7.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
二.填空题(共9小题,满分45分)
8.如图,直线AB∥CD,若∠AEF=85°,∠F=15°,则∠CGF的度数为 .
9.如图,已知BE平分∠ABC,点D在BC延长线上,AB∥CE,若∠ABD=100°,则∠CEB= .
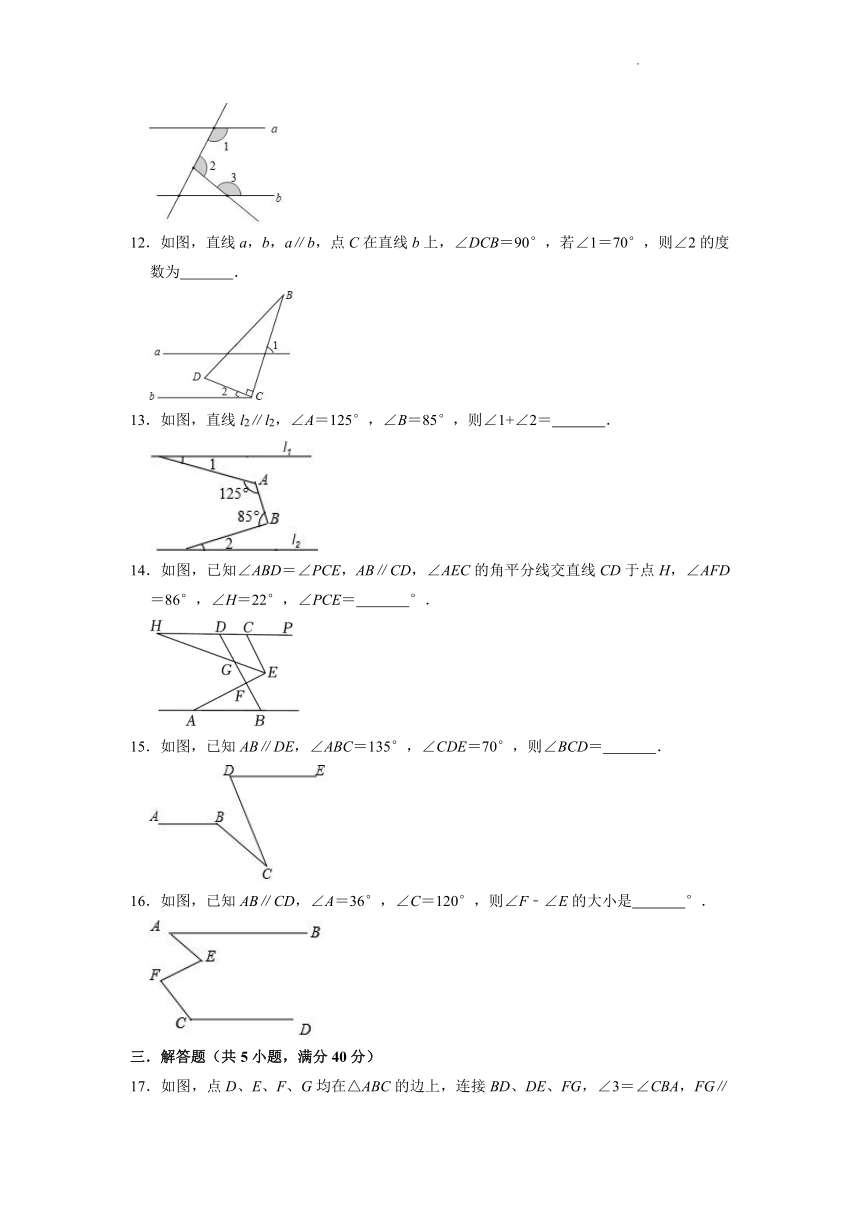
10.如图,已知a∥b,∠1=50°,∠2=115°,则∠3= .
11.如图,已知a∥b,∠2=95°,∠3=140°,则∠1的度数为 .
12.如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为 .
13.如图,直线l2∥l2,∠A=125°,∠B=85°,则∠1+∠2= .
14.如图,已知∠ABD=∠PCE,AB∥CD,∠AEC的角平分线交直线CD于点H,∠AFD=86°,∠H=22°,∠PCE= °.
15.如图,已知AB∥DE,∠ABC=135°,∠CDE=70°,则∠BCD= .
16.如图,已知AB∥CD,∠A=36°,∠C=120°,则∠F﹣∠E的大小是 °.
三.解答题(共5小题,满分40分)
17.如图,点D、E、F、G均在△ABC的边上,连接BD、DE、FG,∠3=∠CBA,FG∥BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
18.如图,已知点D,E分别在△ABC的边AB,AC上,DE∥BC.
(1)若∠ABC=80°,∠AED=40°,求∠A的度数;
(2)若∠BFD+∠CEF=180°,求证:∠EDF=∠C.
19.如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.
(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;
(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).
20.如图,∠ENC+∠CMG=180°,AB∥CD.
(1)求证:∠2=∠3.
(2)若∠A=∠1+70°,∠ACB=42°,则∠B的大小为 .
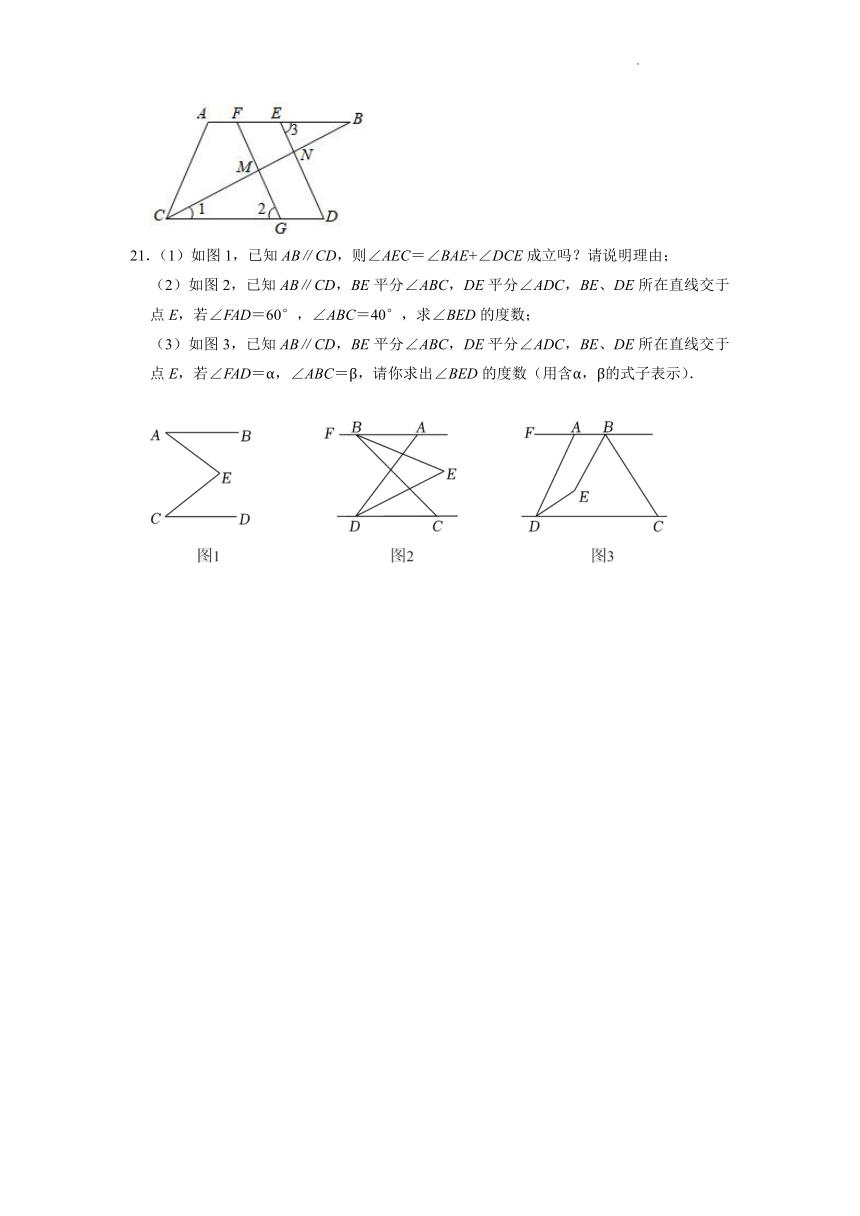
21.(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由;
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠FAD=60°,∠ABC=40°,求∠BED的度数;
(3)如图3,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠FAD=α,∠ABC=β,请你求出∠BED的度数(用含α,β的式子表示).
参考答案
一.选择题(共7小题,满分35分)
1.解:∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°,
过C作CD∥直线m,
∵直线m∥n,
∴CD∥直线m∥直线n,
∴∠1=∠ACD,∠2=∠BCD,
∵∠1=38°,
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
故选:B.
2.解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠2=180°﹣65°=115°.
故选:C.
3.解:∵AB∥CD,
∴∠BEF=180°﹣∠1=180°﹣72°=108°,∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°,
∴∠2=∠BEG=54°.
故选:A.
4.解:
如图,
∵a∥b,
∴∠1=∠C=50°,
又∠1=∠A+∠B,
∴∠A=∠1﹣∠B=50°﹣22°=28°,
故选:B.
5.解:如图,∵长方形纸片ABCD沿EF对折,
∴∠2=∠BFE,
∵∠2+∠BFE+∠1=180°,
∴∠2=(180°﹣40°)=70°,
∵AD∥BC,
∴∠AEF=∠2+∠1=70°+40°=110°.
故选:B.
6.解:如图,分别过K、H作AB的平行线MN和RS,
∵AB∥CD,
∴AB∥CD∥RS∥MN,
∴∠RHB=∠ABE=∠ABK,∠SHC=∠DCF=∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,
∴∠BHC=180°﹣∠RHB﹣∠SHC=180°﹣(∠ABK+∠DCK),
∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,
∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC,
又∵∠BKC﹣∠BHC=27°,
∴∠BHC=∠BKC﹣27°,
∴∠BKC=180°﹣2(∠BKC﹣27°),
∴∠BKC=78°,
故选:C.
7.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
二.填空题(共9小题,满分45分)
8.解:∵∠AEF=85°,∠F=15°,
∴∠AHF=85°﹣15°=70°,
∵AB∥CD,
∴∠CGF=∠AHF=70°.
故答案为:70°.
9.解:∵BE平分∠ABC,∠ABC=100°,
∴∠ABE=∠ABC=50°,
∵AB∥CE,
∴∠CEB=∠ABE=50°,
故答案为50°.
10.解:如图:
∵a∥b,∠1=50°,
∴∠4=∠1=50°,
∵∠2=115°,∠2=∠3+∠4,
∴∠3=∠2﹣∠4=115°﹣50°=65°.
故答案为:65°.
11.解:∵∠3=140°,∠3+∠4=180°,
∴∠4=40°,
∵∠2=95°,∠2=∠5+∠4,
∴∠5=55°,
∵a∥b,
∴∠1+∠5=180°,
∴∠1=125°,
故答案为:125°.
12.解:∵∠1=70°,∠1与∠3是对顶角,
∴∠3=∠1=70°.
∵a∥b,点C在直线b上,∠DCB=90°,
∴∠2+∠DCB+∠3=180°,
∴∠2=180°﹣∠3﹣∠DCB=180°﹣70°﹣90°=20°.
故答案为:20°.
13.解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故答案为30°.
14.解:∵AB∥CD,
∴∠ABD=∠PDB,
∵∠ABD=∠PCE,
∴∠PDB=∠PCE,
∴BD∥CE,
∴∠CEG=∠DGH,
∵EH平分∠AEC,
∴∠CEH=∠AEH,
∵∠DGH=∠EGF,
∴∠EGF=∠GEF,
∵∠AFD=∠AEG+∠EGF=2∠EGF=86°,
∴∠EGF=43°,
∴∠DGH=43°,
∴∠PCE=∠PDG=∠H+∠DGH=65°,
故答案为:65.
15.解:如图,延长CB交ED的延长线于G.
∵AB∥DF,
∴∠1=∠ABC=135°,
∵∠1=∠CDG+∠C,∠CDG=180°﹣∠CDE=110°,
∴∠BCD=135°﹣110°=25°,
故答案为25°.
16.解:如图,过点E作EG∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠A=∠1=36°,∠2=∠3,∠4=180°﹣∠C=180°﹣120°=60°
∴∠EFC﹣∠AEF=∠3+∠4﹣∠1﹣∠2=∠4﹣∠1=60°﹣36°=24°.
故答案为:24.
三.解答题(共5小题,满分40分)
17.解:(1)∵∠3=∠CBA,
∴AB∥DE,
∴∠2=∠DBA,
∵FG∥BD,
∴∠1+∠DBA=180°,
∴∠1+∠2=180°;
(2)∵AB∥DE,
∴∠CDE=∠A=35°,
∵DE平分∠BDC,
∴∠2=∠CDE=35°,
∴∠DBA=35°,
∵BD平分∠CBA,
∴∠CBA=70°,
∴∠C=180°﹣∠A﹣∠CBA=75°.
18.(1)解:∵DE∥BC(已知),
∴∠C=∠AED(两直线平行,同位角相等).
∵∠A+∠ABC+∠C=180°(三角形内角和定理),
∴∠A=180°﹣∠ABC﹣∠C=180°﹣∠ABC﹣∠AED(等式的性质).
∵∠AED=40°,∠ABC=80°(已知),
∴∠A=180°﹣40°﹣80°=60°(等式的性质);
(2)证明:∵∠BFD+∠DFE=180°(平角定义),
∠BFD+∠CEF=180°(已知),
∴∠DFE=∠CEF(同角的补角相等).
∴DF∥AC(内错角相等,两直线平行).
∴∠EDF=∠AED(两直线平行,内错角相等).
∵DE∥BC(已知),
∴∠AED=∠C(两直线平行,同位角相等).
∴∠EDF=∠C(等量代换).
19.解:如图,过点F作FH//CD,
∵锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F,∠ECD=60°,∠ABE=100°,
∴∠DCM=∠ECM=30°,∠ABN=∠EBN=50°°,
∴∠NCF=30°,
∵AB∥CD,FH//CD,
∴FH∥AB,
∴∠HFB=∠ABN=50°,∠HFC=∠FCN=30°,
∴∠BFC=20°.
(2)如图,
∵BF∥CE,
∴∠ECM=∠BFM=α,
∴∠DCE=∠DNB=2α,
∵AB∥CD
∴∠ABN=∠BNC=2α,
∴∠ABE=4α.
20.(1)证明:∵∠ENC+∠CMG=180°,∠FMB=∠CMG,
∴∠ENC+∠ENC=180°,
∴DE∥FG,
∴∠3=∠BFG,
∵AB∥CD,
∴∠BFG=∠2,
∴∠2=∠3;
(2)解:∵AB∥CD,
∴∠A+∠ACD=180°,∠1=∠B,
∵∠A=∠1+70°,∠ACB=42°,
∴∠1+70°+∠ACB+∠1=180°,
即∠1+70°+42°+∠1=180°,
解得:∠1=34°,
∴∠B=∠1=34°.
故答案为:34°.
21.解:(1)成立,
理由:如图1中,作EF//AB,则有EF//CD,
∴∠1=∠BAE,∠2=∠DCE,
∴∠AEC=∠1+∠2=∠BAE+∠DCE;
(2)如图2,过点E作EH//AB,
∵AB//CD,∠FAD=60°,
∴∠FAD=∠ADC=60°,
∵DE平分∠ADC,∠ADC=60°,
∴,
∵BE平分∠ABC,∠ABC=40°,
∴,
∵AB//CD,
∴AB//CD//EH,
∴∠ABE=∠BEH=20°,∠CDE=∠DEH=30°,
∴∠BED=∠BEH+∠DEH=50°.
(3)如图3,过点E作EG//AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=β,∠ADC=∠FAD=α,
∴,,
∵AB//CD,
∴AB//CD//EG,
∴,,
∴.
一.选择题(共7小题,满分35分)
1.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,B分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
2.如图,已知∠1=65°,如果CD∥BE,那么∠B的度数为( )
A.65° B.105° C.115° D.125°
3.如图,直线EF分别交AB、CD于点E、F,EG平分∠BEF,AB∥CD.若∠1=72°,则∠2的度数为( )
A.54° B.59° C.72° D.108°
4.如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
A.22° B.28° C.32° D.38°
5.如图,在平面内,把矩形ABCD沿EF对折,若∠1=40°,则∠AEF等于( )
A.115° B.110° C.120° D.65°
6.如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A.82° B.80° C.78° D.76°
7.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
二.填空题(共9小题,满分45分)
8.如图,直线AB∥CD,若∠AEF=85°,∠F=15°,则∠CGF的度数为 .
9.如图,已知BE平分∠ABC,点D在BC延长线上,AB∥CE,若∠ABD=100°,则∠CEB= .
10.如图,已知a∥b,∠1=50°,∠2=115°,则∠3= .
11.如图,已知a∥b,∠2=95°,∠3=140°,则∠1的度数为 .
12.如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为 .
13.如图,直线l2∥l2,∠A=125°,∠B=85°,则∠1+∠2= .
14.如图,已知∠ABD=∠PCE,AB∥CD,∠AEC的角平分线交直线CD于点H,∠AFD=86°,∠H=22°,∠PCE= °.
15.如图,已知AB∥DE,∠ABC=135°,∠CDE=70°,则∠BCD= .
16.如图,已知AB∥CD,∠A=36°,∠C=120°,则∠F﹣∠E的大小是 °.
三.解答题(共5小题,满分40分)
17.如图,点D、E、F、G均在△ABC的边上,连接BD、DE、FG,∠3=∠CBA,FG∥BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
18.如图,已知点D,E分别在△ABC的边AB,AC上,DE∥BC.
(1)若∠ABC=80°,∠AED=40°,求∠A的度数;
(2)若∠BFD+∠CEF=180°,求证:∠EDF=∠C.
19.如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.
(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;
(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).
20.如图,∠ENC+∠CMG=180°,AB∥CD.
(1)求证:∠2=∠3.
(2)若∠A=∠1+70°,∠ACB=42°,则∠B的大小为 .
21.(1)如图1,已知AB∥CD,则∠AEC=∠BAE+∠DCE成立吗?请说明理由;
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠FAD=60°,∠ABC=40°,求∠BED的度数;
(3)如图3,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,若∠FAD=α,∠ABC=β,请你求出∠BED的度数(用含α,β的式子表示).
参考答案
一.选择题(共7小题,满分35分)
1.解:∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°,
过C作CD∥直线m,
∵直线m∥n,
∴CD∥直线m∥直线n,
∴∠1=∠ACD,∠2=∠BCD,
∵∠1=38°,
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
故选:B.
2.解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠2=180°﹣65°=115°.
故选:C.
3.解:∵AB∥CD,
∴∠BEF=180°﹣∠1=180°﹣72°=108°,∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°,
∴∠2=∠BEG=54°.
故选:A.
4.解:
如图,
∵a∥b,
∴∠1=∠C=50°,
又∠1=∠A+∠B,
∴∠A=∠1﹣∠B=50°﹣22°=28°,
故选:B.
5.解:如图,∵长方形纸片ABCD沿EF对折,
∴∠2=∠BFE,
∵∠2+∠BFE+∠1=180°,
∴∠2=(180°﹣40°)=70°,
∵AD∥BC,
∴∠AEF=∠2+∠1=70°+40°=110°.
故选:B.
6.解:如图,分别过K、H作AB的平行线MN和RS,
∵AB∥CD,
∴AB∥CD∥RS∥MN,
∴∠RHB=∠ABE=∠ABK,∠SHC=∠DCF=∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,
∴∠BHC=180°﹣∠RHB﹣∠SHC=180°﹣(∠ABK+∠DCK),
∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,
∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC,
又∵∠BKC﹣∠BHC=27°,
∴∠BHC=∠BKC﹣27°,
∴∠BKC=180°﹣2(∠BKC﹣27°),
∴∠BKC=78°,
故选:C.
7.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
二.填空题(共9小题,满分45分)
8.解:∵∠AEF=85°,∠F=15°,
∴∠AHF=85°﹣15°=70°,
∵AB∥CD,
∴∠CGF=∠AHF=70°.
故答案为:70°.
9.解:∵BE平分∠ABC,∠ABC=100°,
∴∠ABE=∠ABC=50°,
∵AB∥CE,
∴∠CEB=∠ABE=50°,
故答案为50°.
10.解:如图:
∵a∥b,∠1=50°,
∴∠4=∠1=50°,
∵∠2=115°,∠2=∠3+∠4,
∴∠3=∠2﹣∠4=115°﹣50°=65°.
故答案为:65°.
11.解:∵∠3=140°,∠3+∠4=180°,
∴∠4=40°,
∵∠2=95°,∠2=∠5+∠4,
∴∠5=55°,
∵a∥b,
∴∠1+∠5=180°,
∴∠1=125°,
故答案为:125°.
12.解:∵∠1=70°,∠1与∠3是对顶角,
∴∠3=∠1=70°.
∵a∥b,点C在直线b上,∠DCB=90°,
∴∠2+∠DCB+∠3=180°,
∴∠2=180°﹣∠3﹣∠DCB=180°﹣70°﹣90°=20°.
故答案为:20°.
13.解:如图,过点A作l1的平行线,过点B作l2的平行线,
∴∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故答案为30°.
14.解:∵AB∥CD,
∴∠ABD=∠PDB,
∵∠ABD=∠PCE,
∴∠PDB=∠PCE,
∴BD∥CE,
∴∠CEG=∠DGH,
∵EH平分∠AEC,
∴∠CEH=∠AEH,
∵∠DGH=∠EGF,
∴∠EGF=∠GEF,
∵∠AFD=∠AEG+∠EGF=2∠EGF=86°,
∴∠EGF=43°,
∴∠DGH=43°,
∴∠PCE=∠PDG=∠H+∠DGH=65°,
故答案为:65.
15.解:如图,延长CB交ED的延长线于G.
∵AB∥DF,
∴∠1=∠ABC=135°,
∵∠1=∠CDG+∠C,∠CDG=180°﹣∠CDE=110°,
∴∠BCD=135°﹣110°=25°,
故答案为25°.
16.解:如图,过点E作EG∥AB,过点F作FH∥AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠A=∠1=36°,∠2=∠3,∠4=180°﹣∠C=180°﹣120°=60°
∴∠EFC﹣∠AEF=∠3+∠4﹣∠1﹣∠2=∠4﹣∠1=60°﹣36°=24°.
故答案为:24.
三.解答题(共5小题,满分40分)
17.解:(1)∵∠3=∠CBA,
∴AB∥DE,
∴∠2=∠DBA,
∵FG∥BD,
∴∠1+∠DBA=180°,
∴∠1+∠2=180°;
(2)∵AB∥DE,
∴∠CDE=∠A=35°,
∵DE平分∠BDC,
∴∠2=∠CDE=35°,
∴∠DBA=35°,
∵BD平分∠CBA,
∴∠CBA=70°,
∴∠C=180°﹣∠A﹣∠CBA=75°.
18.(1)解:∵DE∥BC(已知),
∴∠C=∠AED(两直线平行,同位角相等).
∵∠A+∠ABC+∠C=180°(三角形内角和定理),
∴∠A=180°﹣∠ABC﹣∠C=180°﹣∠ABC﹣∠AED(等式的性质).
∵∠AED=40°,∠ABC=80°(已知),
∴∠A=180°﹣40°﹣80°=60°(等式的性质);
(2)证明:∵∠BFD+∠DFE=180°(平角定义),
∠BFD+∠CEF=180°(已知),
∴∠DFE=∠CEF(同角的补角相等).
∴DF∥AC(内错角相等,两直线平行).
∴∠EDF=∠AED(两直线平行,内错角相等).
∵DE∥BC(已知),
∴∠AED=∠C(两直线平行,同位角相等).
∴∠EDF=∠C(等量代换).
19.解:如图,过点F作FH//CD,
∵锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F,∠ECD=60°,∠ABE=100°,
∴∠DCM=∠ECM=30°,∠ABN=∠EBN=50°°,
∴∠NCF=30°,
∵AB∥CD,FH//CD,
∴FH∥AB,
∴∠HFB=∠ABN=50°,∠HFC=∠FCN=30°,
∴∠BFC=20°.
(2)如图,
∵BF∥CE,
∴∠ECM=∠BFM=α,
∴∠DCE=∠DNB=2α,
∵AB∥CD
∴∠ABN=∠BNC=2α,
∴∠ABE=4α.
20.(1)证明:∵∠ENC+∠CMG=180°,∠FMB=∠CMG,
∴∠ENC+∠ENC=180°,
∴DE∥FG,
∴∠3=∠BFG,
∵AB∥CD,
∴∠BFG=∠2,
∴∠2=∠3;
(2)解:∵AB∥CD,
∴∠A+∠ACD=180°,∠1=∠B,
∵∠A=∠1+70°,∠ACB=42°,
∴∠1+70°+∠ACB+∠1=180°,
即∠1+70°+42°+∠1=180°,
解得:∠1=34°,
∴∠B=∠1=34°.
故答案为:34°.
21.解:(1)成立,
理由:如图1中,作EF//AB,则有EF//CD,
∴∠1=∠BAE,∠2=∠DCE,
∴∠AEC=∠1+∠2=∠BAE+∠DCE;
(2)如图2,过点E作EH//AB,
∵AB//CD,∠FAD=60°,
∴∠FAD=∠ADC=60°,
∵DE平分∠ADC,∠ADC=60°,
∴,
∵BE平分∠ABC,∠ABC=40°,
∴,
∵AB//CD,
∴AB//CD//EH,
∴∠ABE=∠BEH=20°,∠CDE=∠DEH=30°,
∴∠BED=∠BEH+∠DEH=50°.
(3)如图3,过点E作EG//AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=β,∠ADC=∠FAD=α,
∴,,
∵AB//CD,
∴AB//CD//EG,
∴,,
∴.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
