2.4二元一次方程组的应用 课件(共20张PPT)
文档属性
| 名称 | 2.4二元一次方程组的应用 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 08:41:42 | ||
图片预览







文档简介
(共20张PPT)
2.4二元一次方程组的应用
第1课时
浙教版 七年级下
新知导入
48名同学被分配到大、小不同的两种寝室,大寝室每间住8人,小寝室每间住4人,刚好住满.求大、小寝室各住了多少间.
思考:
(1)问题中有几个未知量?
(2)有几个等量关系?
(3)如果设一个未知数,能列出方程吗?
(4)如果设两个未知数,能列出几个方程?能确定方程的解吗?
两个
一个:8×大寝室间数+4×小寝室间数=48
不能
设大寝室住了x间,小寝室住了y间,
则:8x+4y=48
方程的解不唯一确定!
二元一次方程是不定方程
(5)你能添加一个条件,使该问题有唯一确定的解吗
已知量
未知量
那问题的解呢?
48名同学被分配到大、小不同的两种寝室,大寝室每间住8人,小寝室每间住4人,刚好住满,且大、小寝室共住了9间.求大、小寝室各住了多少间.
解:设大寝室住了x间,小寝室住了y间.
根据题意,得
化简①,得 2x+y=12 ③
①
②
③-②,得 x=3.
把x=3 代入②,解得 y=6.
∴方程组的解为
经检验,这个解满足方程组,且符合题意.
答:大寝室住了3间,小寝室住了6间.
加减
消元法
可以列一元一次方程吗?
可以,相当于运用了代入消元法.
新知导入
课堂小结
要点小结1:
当问题所求的未知量有两个时,必须寻找到两个等量关系,方程才有确定的解.
设一个未知数→列一元一次方程
设两个未知数→列二元一次方程组
两种策略
体会设两个未知数的好处
合作学习
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
思考:
(1)问题中有几个未知量?
(2)你能正确写出等量关系吗?
(3)你会怎样设未知数呢?
男孩人数-1=女孩人数
男孩人数=2(女孩人数-1)
(4)你能列二元一次方程组来解决问题吗?
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
男孩人数-1=女孩人数
男孩人数=2(女孩人数-1)
解:设男孩有x人,女孩有y人,根据题意,得
解得:
经检验,这个解满足方程组,且符合题意.
答:男孩有4人,女孩有3人.
要点小结2:设两个未知数更容易列出方程.
合作学习
课堂小结
列二元一次方程组解应用题的一般步骤:
审→设→找→列→解→检→答.
(1)审:通过审题,搞清已知和未知,理解数量关系;
(2)设:用字母表示其中的两个未知量(设元);
(3)找:找到两个相等关系;
(4)列:根据两个等量关系列出方程组;
(5)解:解这个方程组,求出未知数的值;
(6)检:检验所得的解是否符合实际意义;
(7)答:写出答案.
例题讲解
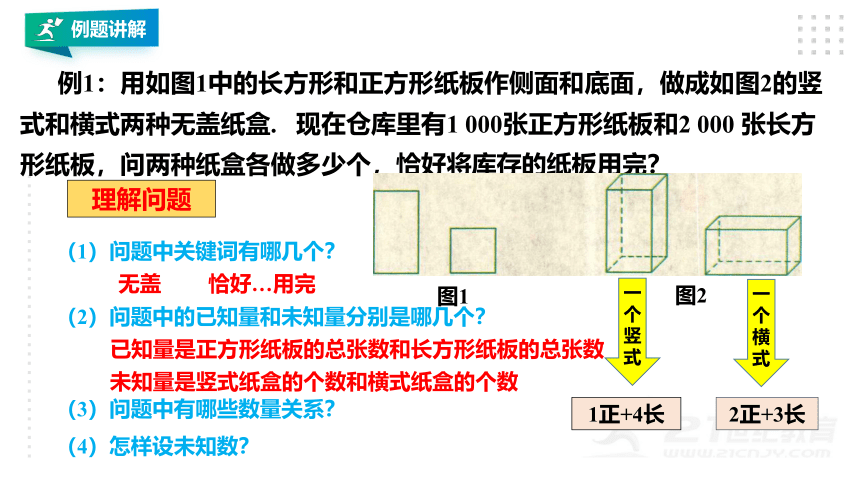
例1:用如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒. 现在仓库里有1 000张正方形纸板和2 000 张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?
图1
图2
理解问题
(1)问题中关键词有哪几个?
(2)问题中的已知量和未知量分别是哪几个?
(3)问题中有哪些数量关系?
无盖
恰好…用完
(4)怎样设未知数?
已知量是正方形纸板的总张数和长方形纸板的总张数
未知量是竖式纸盒的个数和横式纸盒的个数
一个竖式
一个横式
1正+4长
2正+3长
例题讲解
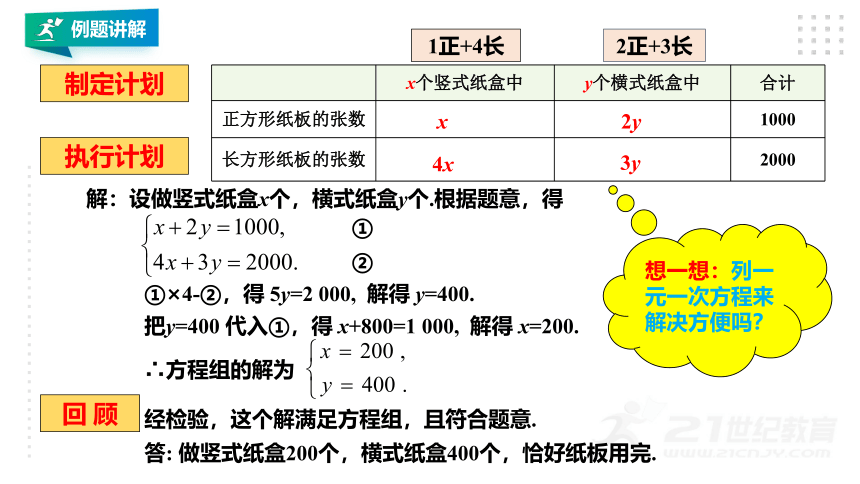
制定计划
x个竖式纸盒中 y个横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
解:设做竖式纸盒x个,横式纸盒y个.根据题意,得
x
4x
2y
3y
①
②
①×4-②,得 5y=2 000, 解得 y=400.
把y=400 代入①,得 x+800=1 000, 解得 x=200.
经检验,这个解满足方程组,且符合题意.
答: 做竖式纸盒200个,横式纸盒400个,恰好纸板用完.
∴方程组的解为
执行计划
回 顾
想一想:列一元一次方程来解决方便吗?
1正+4长
2正+3长
变式练习
变式:用如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒. 现在仓库里有500张正方形纸板和1001张长方形纸板,那么能否在做成若干只这两种纸盒后,恰好将库存的纸板用完?
图1
图2
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
x
4x
2y
3y
500
1001
解:设做竖式纸盒x个,横式纸盒y个
时能恰好用完.则
①×4-②,得 5y=999,
①
②
显然,y不是自然数,不合题意.所以不可能做成若干只纸盒后,恰好把库存的纸板用完.
课堂小结
要点小结3
实际问题
数学问题
列方程(组)
抽象:用字母表示数(设未知数)
建模:方程(组)是刻画等量关系的模型
检验,作答
“能不能”
“是否存在”
方程的解是否符合题意
理解问题
制定计划
执行计划
回 顾
课内练习
1.一个水坝的横截面是梯形,它的面积为42m2,高为6m,下底比上底的2倍少1m,
则上底和下底的长各是多少米?
42m2
6m
等量关系:
下底=2×上底-1
(上底+下底)×6÷2=42
设上底为x米,下底为y米,可列方程组:
解得:
经检验,这个解满足方程组,且符合题意.
答: 上底是5米,下底是9米.
共15分钟
2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟. 问:从小华家到学校有多远?
解:设小华从家里到学校平路有x米,下坡路有y米,
所以,小华家到学校的距离为 300+400=700(米)
由题意得
∴方程组的解为
经检验,这个解满足方程组,且符合题意.
①
②
②-①,得 ,解得 y=400.
把y=400 代入①,解得 x=300.
下坡
上坡
共10分钟
学校
家
你还有其他方法吗?
课内练习
共15分钟
2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟. 问:从小华家到学校有多远?
下坡
上坡
共10分钟
学校
家
解法2:设下坡路为y米,根据题意,得
解得 y=400.
经检验,这个解满足方程组,且符合题意.
∴60×(10-400÷80)+400=700(米)
答:小华家到学校的距离为 700米.
进行了加减消元
你还有其他方法吗?
课内练习
共15分钟
2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟. 问:从小华家到学校有多远?
∴60×5+80×(10-5)=700(米)
经检验,这个解满足方程组,且符合题意.
下坡
上坡
共10分钟
学校
家
体会:设两个未知数更容易列出方程
解法3:设小华走平路上需要t分钟,根据题意,得
(10-t)分钟
(15-t)分钟
解得 t=5.
答:小华家到学校的距离为 700米.
对比等量关系的获得,你发现了什么?
你还有其他方法吗?
课内练习
3.图①的等臂天平呈平衡状态,其中左侧秤盘有一袋石头,右侧秤盘有一
袋石头和2个各10克的砝码.将左侧袋中一颗石头移至右侧秤盘,并拿
走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图②所示.则被移动
石头的质量为( )
A.5克 B.10克 C.15克 D.20克
A
问题中有几个未知量?几个等量关系?
x
y
z
①
②
②-①,得 -z=-10+z,
解得 z=5.
设三个未知数更容易列出方程,解方程组基本思路是消元
拓展提升
课堂总结
实际问题
实际问题的答案
数学问题
(二元一次方程组)
有两个未知量
(设两个未知数)
数学问题的解
(二元一次方程组的解)
解二元一次方程组
代入法
加减法
(消元)
检验,作答
寻找两个等量关系
更容易列出方程
列表分析、画行程图等帮助我们找到等量关系
回顾环节不要忽视
作业布置
作业本(1)2.4二元一次方程组的应用(1)
https://www.21cnjy.com/help/help_extract.php
2.4二元一次方程组的应用
第1课时
浙教版 七年级下
新知导入
48名同学被分配到大、小不同的两种寝室,大寝室每间住8人,小寝室每间住4人,刚好住满.求大、小寝室各住了多少间.
思考:
(1)问题中有几个未知量?
(2)有几个等量关系?
(3)如果设一个未知数,能列出方程吗?
(4)如果设两个未知数,能列出几个方程?能确定方程的解吗?
两个
一个:8×大寝室间数+4×小寝室间数=48
不能
设大寝室住了x间,小寝室住了y间,
则:8x+4y=48
方程的解不唯一确定!
二元一次方程是不定方程
(5)你能添加一个条件,使该问题有唯一确定的解吗
已知量
未知量
那问题的解呢?
48名同学被分配到大、小不同的两种寝室,大寝室每间住8人,小寝室每间住4人,刚好住满,且大、小寝室共住了9间.求大、小寝室各住了多少间.
解:设大寝室住了x间,小寝室住了y间.
根据题意,得
化简①,得 2x+y=12 ③
①
②
③-②,得 x=3.
把x=3 代入②,解得 y=6.
∴方程组的解为
经检验,这个解满足方程组,且符合题意.
答:大寝室住了3间,小寝室住了6间.
加减
消元法
可以列一元一次方程吗?
可以,相当于运用了代入消元法.
新知导入
课堂小结
要点小结1:
当问题所求的未知量有两个时,必须寻找到两个等量关系,方程才有确定的解.
设一个未知数→列一元一次方程
设两个未知数→列二元一次方程组
两种策略
体会设两个未知数的好处
合作学习
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
思考:
(1)问题中有几个未知量?
(2)你能正确写出等量关系吗?
(3)你会怎样设未知数呢?
男孩人数-1=女孩人数
男孩人数=2(女孩人数-1)
(4)你能列二元一次方程组来解决问题吗?
游泳池中有一群小朋友,男孩戴蓝色游泳帽,女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多, 而每位女孩看到蓝色的游泳帽比红色的多1倍,你知道男孩与女孩各有多少人吗?
男孩人数-1=女孩人数
男孩人数=2(女孩人数-1)
解:设男孩有x人,女孩有y人,根据题意,得
解得:
经检验,这个解满足方程组,且符合题意.
答:男孩有4人,女孩有3人.
要点小结2:设两个未知数更容易列出方程.
合作学习
课堂小结
列二元一次方程组解应用题的一般步骤:
审→设→找→列→解→检→答.
(1)审:通过审题,搞清已知和未知,理解数量关系;
(2)设:用字母表示其中的两个未知量(设元);
(3)找:找到两个相等关系;
(4)列:根据两个等量关系列出方程组;
(5)解:解这个方程组,求出未知数的值;
(6)检:检验所得的解是否符合实际意义;
(7)答:写出答案.
例题讲解
例1:用如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒. 现在仓库里有1 000张正方形纸板和2 000 张长方形纸板,问两种纸盒各做多少个,恰好将库存的纸板用完?
图1
图2
理解问题
(1)问题中关键词有哪几个?
(2)问题中的已知量和未知量分别是哪几个?
(3)问题中有哪些数量关系?
无盖
恰好…用完
(4)怎样设未知数?
已知量是正方形纸板的总张数和长方形纸板的总张数
未知量是竖式纸盒的个数和横式纸盒的个数
一个竖式
一个横式
1正+4长
2正+3长
例题讲解
制定计划
x个竖式纸盒中 y个横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
解:设做竖式纸盒x个,横式纸盒y个.根据题意,得
x
4x
2y
3y
①
②
①×4-②,得 5y=2 000, 解得 y=400.
把y=400 代入①,得 x+800=1 000, 解得 x=200.
经检验,这个解满足方程组,且符合题意.
答: 做竖式纸盒200个,横式纸盒400个,恰好纸板用完.
∴方程组的解为
执行计划
回 顾
想一想:列一元一次方程来解决方便吗?
1正+4长
2正+3长
变式练习
变式:用如图1中的长方形和正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒. 现在仓库里有500张正方形纸板和1001张长方形纸板,那么能否在做成若干只这两种纸盒后,恰好将库存的纸板用完?
图1
图2
x只竖式纸盒中 y只横式纸盒中 合计
正方形纸板的张数 1000
长方形纸板的张数 2000
x
4x
2y
3y
500
1001
解:设做竖式纸盒x个,横式纸盒y个
时能恰好用完.则
①×4-②,得 5y=999,
①
②
显然,y不是自然数,不合题意.所以不可能做成若干只纸盒后,恰好把库存的纸板用完.
课堂小结
要点小结3
实际问题
数学问题
列方程(组)
抽象:用字母表示数(设未知数)
建模:方程(组)是刻画等量关系的模型
检验,作答
“能不能”
“是否存在”
方程的解是否符合题意
理解问题
制定计划
执行计划
回 顾
课内练习
1.一个水坝的横截面是梯形,它的面积为42m2,高为6m,下底比上底的2倍少1m,
则上底和下底的长各是多少米?
42m2
6m
等量关系:
下底=2×上底-1
(上底+下底)×6÷2=42
设上底为x米,下底为y米,可列方程组:
解得:
经检验,这个解满足方程组,且符合题意.
答: 上底是5米,下底是9米.
共15分钟
2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟. 问:从小华家到学校有多远?
解:设小华从家里到学校平路有x米,下坡路有y米,
所以,小华家到学校的距离为 300+400=700(米)
由题意得
∴方程组的解为
经检验,这个解满足方程组,且符合题意.
①
②
②-①,得 ,解得 y=400.
把y=400 代入①,解得 x=300.
下坡
上坡
共10分钟
学校
家
你还有其他方法吗?
课内练习
共15分钟
2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟. 问:从小华家到学校有多远?
下坡
上坡
共10分钟
学校
家
解法2:设下坡路为y米,根据题意,得
解得 y=400.
经检验,这个解满足方程组,且符合题意.
∴60×(10-400÷80)+400=700(米)
答:小华家到学校的距离为 700米.
进行了加减消元
你还有其他方法吗?
课内练习
共15分钟
2.小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60 米,下坡路每分钟走80米,上坡路每分钟走40米,则他从家里到学校需10分钟,从学校到家里需15分钟. 问:从小华家到学校有多远?
∴60×5+80×(10-5)=700(米)
经检验,这个解满足方程组,且符合题意.
下坡
上坡
共10分钟
学校
家
体会:设两个未知数更容易列出方程
解法3:设小华走平路上需要t分钟,根据题意,得
(10-t)分钟
(15-t)分钟
解得 t=5.
答:小华家到学校的距离为 700米.
对比等量关系的获得,你发现了什么?
你还有其他方法吗?
课内练习
3.图①的等臂天平呈平衡状态,其中左侧秤盘有一袋石头,右侧秤盘有一
袋石头和2个各10克的砝码.将左侧袋中一颗石头移至右侧秤盘,并拿
走右侧秤盘的1个砝码后,天平仍呈平衡状态,如图②所示.则被移动
石头的质量为( )
A.5克 B.10克 C.15克 D.20克
A
问题中有几个未知量?几个等量关系?
x
y
z
①
②
②-①,得 -z=-10+z,
解得 z=5.
设三个未知数更容易列出方程,解方程组基本思路是消元
拓展提升
课堂总结
实际问题
实际问题的答案
数学问题
(二元一次方程组)
有两个未知量
(设两个未知数)
数学问题的解
(二元一次方程组的解)
解二元一次方程组
代入法
加减法
(消元)
检验,作答
寻找两个等量关系
更容易列出方程
列表分析、画行程图等帮助我们找到等量关系
回顾环节不要忽视
作业布置
作业本(1)2.4二元一次方程组的应用(1)
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
