2.3二元一次方程组解法巩固 课件(共26张PPT)
文档属性
| 名称 | 2.3二元一次方程组解法巩固 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 08:35:33 | ||
图片预览





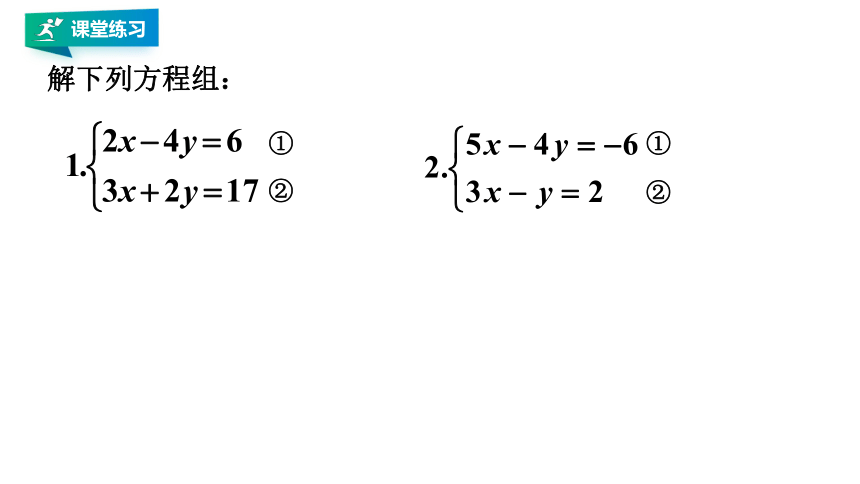

文档简介
(共26张PPT)
二元一次方程组解法巩固
浙教版 七年级下
1.在解方程组 时,可以直接把___ 代入___,
就可消去未知数___.
2.在解方程组 时,可以先将___变形为________ ,
再代入___,就可消去未知数___
①
②
①
②
①
②
y
①
y=2-3x
②
y
课堂练习
3.用加减法解方程组 ,①-②得( )
(A) (B) (C) (D)
①
②
4.已知方程组 ,用加减法消x的方法是__________;
用加减法消y的方法是________.
B
①
②
②×2-①×3
①×2+②×3
课堂练习
【问题1】你怎样解下面的方程组?
①
②
x的系数为1
代入法
解:由①,得
x=3y+5 ③
把③代入②,得
4(3y+5)-3y=2
解得:
y=﹣2
把y=﹣2代入③得:
x=3×(-2)+5=-1
∴原方程组的解是
一变形
1.用含一个未知数的代数式
表示另一个未知数
二代入
2.消去一个元
三求解
四回代
3.分别求出两个
未知数的值
五写解
六检验
4.写出方程组的解
课堂练习
【问题1】你怎样解下面的方程组?
①
②
y的系数为相同
加减法
解:②-①,得
3x=-3
解得:
x =-1
把x=﹣1代入①得:
-1-3y=5
∴原方程组的解是
一变形
1.同一个未知数的系数相同 或互为相反数
二加减
2.消去一个元
三求解
3.分别求出两个未知数的值
四写解
五检验
4.写出方程组的解
解得:
y=﹣2
课堂练习
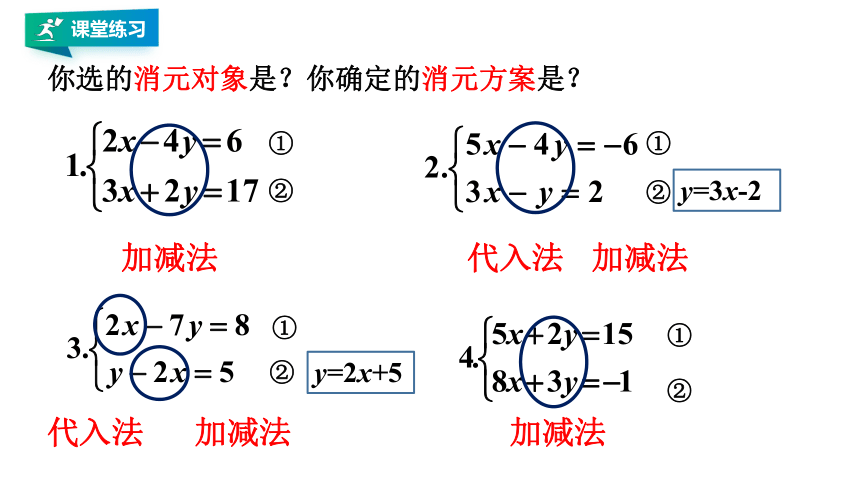
你选的消元对象是?你确定的消元方案是?
①
②
①
②
①
②
①
②
加减法
加减法
代入法
加减法
代入法
y=2x+5
加减法
y=3x-2
课堂练习
①
②
①
②
①
②
①
②
加减法
加减法
代入法
加减法
代入法
加减法
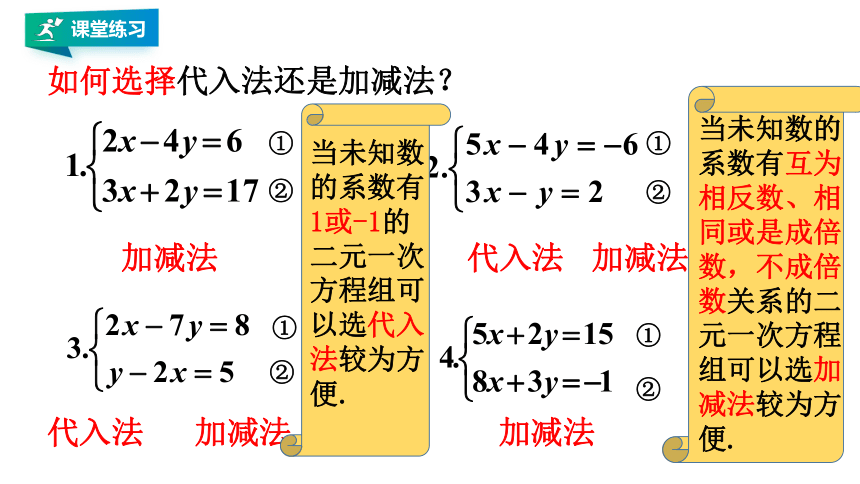
如何选择代入法还是加减法?
当未知数的系数有1或-1的二元一次方程组可以选代入法较为方便.
当未知数的系数有互为相反数、相同或是成倍数,不成倍数关系的二元一次方程组可以选加减法较为方便.
课堂练习
解下列方程组:
①
②
①
②
课堂练习
解下列方程组:
①
②
解:②×2,得:6x+4y=34 ③
①+③,得:8x=40
解得:x=5
把x=5代入①得:2×5-4y=6
解得:y=1
∴原方程组的解为x=5,y=1
解:①×3,得:6x-12y=18 ③
②×2,得:6x+4y=34 ④
④-③,得:-8y=16
解得:y=-2
把y=-2代入①得:2x-4×(-2)=6
解得:x=-1
∴原方程组的解为
二元一次方程组的解的规范表示.
课堂练习
解下列方程组:
①
②
解:由②得:y=3x-2 ③
把③代入①,得:
5x-4(3x-2)=-6
解得:x=2
把x=2代入③得:y=3×2-2=4
∴原方程组的解为
解:②×4,得:12x-4y=8 ③
①-③,得:7x=-14
解得:x=-2
把x=-2代入③得:12×(-2)-4y=8
解得:y=-8
∴原方程组的解为
两式相减的时候注意符号处理.
课堂练习
解下列方程组:
①
②
①
②
①
②
这个方程组与前两个有什么不同?
应该怎样解答?
课堂练习
解下列方程组:
解:把原方程整理得:
①
②
②-①,得:3y=9
解得:y=3
把y=3代入①得:3x-3=9
解得:x=4
∴原方程组的解为
当方程组较为复杂时,有括号或分母时,可以化繁为简,整理方程后再选择恰当的方法消元求解.
课堂练习
解下列方程组:
解法1:把原方程整理得:
①
②
当方程组里两个方程都含有一个相同的整式时,也可以采取整体代入法,化繁为简.
解法2:直接把①代入②得:
课堂练习
【问题1】你怎样解下面的方程组?
①
②
这个方程组可以利用整体代入法进行求解吗?
解:由②,得
3x+x-3y=2 ③
把①代入③,得
3x+5=2
解得:
x=-1
∴原方程组的解是
把x=-1代入①得:
-1﹣3y=5
解得:y=﹣2
一题多解
整体代入
课堂练习
【问题2】你怎样解下面的方程组?
①
②
解法1:①×3-②×2
观察这个方程组两个未知数的系数有何特征?
解法2:①+②得:5x+5y=9 即x+y=1.8 ③
②-①得:x-y=1 ④
③+④得:2x=2.8 ∴x=1.4
③-④得:2y=0.8 ∴y=0.4
∴原方程组的解是
当两个方程中未知数的系数恰好互换时,可以先把这两个方程分别相加、相减,达到求解的目的.
课堂练习
整体加减再认识
4x+4y=20
两个方程直接相加
x+y=5
两个方程直接相减
m-3n=-3
整体加减直接求值
课堂练习
三位同学分别提出了以下三种不同的解题思路:
课堂练习
解:①×2,得:4x+6y=8 ③
②×3,得:9x+6y=6m-9 ④
④-③,得:5x=6m-17
解得:x=
把x= 代入①得:
解得:
①
②
甲同学是直接根据方程组的解的概念先解方程组,得到用含m的式子表示x、y的表达式,再代入x-y=1得到关于m的方程,没有经过更多的观察和思考,解法比较繁琐,计算量大;
课堂练习
①
②
乙同学:先将方程组中的两个方程相减,再求m的值.
乙同学观察到了方程组中未知数x、y的系数,以及与x-y=1中的系数的特殊关系,利用整体代入简化计算,而且不用求出x、y的值就能解决问题,思路比较灵活,计算量小;
解:②-①,得:x-y=2m-7
∵x-y=1
∴2m-7=1
∴m=4
课堂练习
丙同学将三个方程做为一个整体,看成关于x,y的一次方程组,并且选择先解其中不含字母参数的x,y的二元一次方程组,相对计算量较小,但不如乙同学的简洁、灵活.
课堂练习
乙同学:先将方程组中的两个方程相加,再求m的值.
方法最佳,整体加减运用有条件限制.
方法相对繁琐,但是是解题的通法.
方法可行,重新组合也有条件限制.
学会观察思考,灵活解题,一题多解,选择最佳解题方法.
课堂练习
二元一次方程组
一元一次 方程
消元法
转化
代入消元法
加减消元法
整体代入
整体加减
整体思想
化繁为简
方程组的系数有绝对值为1
方程组的系数有绝对值相同,成倍数等
三元一次方程组
一元二次方程
消元
降次
整体思想
转化思想
一题多解
举一反三
课堂练习
课堂练习
课堂练习
https://www.21cnjy.com/help/help_extract.php
二元一次方程组解法巩固
浙教版 七年级下
1.在解方程组 时,可以直接把___ 代入___,
就可消去未知数___.
2.在解方程组 时,可以先将___变形为________ ,
再代入___,就可消去未知数___
①
②
①
②
①
②
y
①
y=2-3x
②
y
课堂练习
3.用加减法解方程组 ,①-②得( )
(A) (B) (C) (D)
①
②
4.已知方程组 ,用加减法消x的方法是__________;
用加减法消y的方法是________.
B
①
②
②×2-①×3
①×2+②×3
课堂练习
【问题1】你怎样解下面的方程组?
①
②
x的系数为1
代入法
解:由①,得
x=3y+5 ③
把③代入②,得
4(3y+5)-3y=2
解得:
y=﹣2
把y=﹣2代入③得:
x=3×(-2)+5=-1
∴原方程组的解是
一变形
1.用含一个未知数的代数式
表示另一个未知数
二代入
2.消去一个元
三求解
四回代
3.分别求出两个
未知数的值
五写解
六检验
4.写出方程组的解
课堂练习
【问题1】你怎样解下面的方程组?
①
②
y的系数为相同
加减法
解:②-①,得
3x=-3
解得:
x =-1
把x=﹣1代入①得:
-1-3y=5
∴原方程组的解是
一变形
1.同一个未知数的系数相同 或互为相反数
二加减
2.消去一个元
三求解
3.分别求出两个未知数的值
四写解
五检验
4.写出方程组的解
解得:
y=﹣2
课堂练习
你选的消元对象是?你确定的消元方案是?
①
②
①
②
①
②
①
②
加减法
加减法
代入法
加减法
代入法
y=2x+5
加减法
y=3x-2
课堂练习
①
②
①
②
①
②
①
②
加减法
加减法
代入法
加减法
代入法
加减法
如何选择代入法还是加减法?
当未知数的系数有1或-1的二元一次方程组可以选代入法较为方便.
当未知数的系数有互为相反数、相同或是成倍数,不成倍数关系的二元一次方程组可以选加减法较为方便.
课堂练习
解下列方程组:
①
②
①
②
课堂练习
解下列方程组:
①
②
解:②×2,得:6x+4y=34 ③
①+③,得:8x=40
解得:x=5
把x=5代入①得:2×5-4y=6
解得:y=1
∴原方程组的解为x=5,y=1
解:①×3,得:6x-12y=18 ③
②×2,得:6x+4y=34 ④
④-③,得:-8y=16
解得:y=-2
把y=-2代入①得:2x-4×(-2)=6
解得:x=-1
∴原方程组的解为
二元一次方程组的解的规范表示.
课堂练习
解下列方程组:
①
②
解:由②得:y=3x-2 ③
把③代入①,得:
5x-4(3x-2)=-6
解得:x=2
把x=2代入③得:y=3×2-2=4
∴原方程组的解为
解:②×4,得:12x-4y=8 ③
①-③,得:7x=-14
解得:x=-2
把x=-2代入③得:12×(-2)-4y=8
解得:y=-8
∴原方程组的解为
两式相减的时候注意符号处理.
课堂练习
解下列方程组:
①
②
①
②
①
②
这个方程组与前两个有什么不同?
应该怎样解答?
课堂练习
解下列方程组:
解:把原方程整理得:
①
②
②-①,得:3y=9
解得:y=3
把y=3代入①得:3x-3=9
解得:x=4
∴原方程组的解为
当方程组较为复杂时,有括号或分母时,可以化繁为简,整理方程后再选择恰当的方法消元求解.
课堂练习
解下列方程组:
解法1:把原方程整理得:
①
②
当方程组里两个方程都含有一个相同的整式时,也可以采取整体代入法,化繁为简.
解法2:直接把①代入②得:
课堂练习
【问题1】你怎样解下面的方程组?
①
②
这个方程组可以利用整体代入法进行求解吗?
解:由②,得
3x+x-3y=2 ③
把①代入③,得
3x+5=2
解得:
x=-1
∴原方程组的解是
把x=-1代入①得:
-1﹣3y=5
解得:y=﹣2
一题多解
整体代入
课堂练习
【问题2】你怎样解下面的方程组?
①
②
解法1:①×3-②×2
观察这个方程组两个未知数的系数有何特征?
解法2:①+②得:5x+5y=9 即x+y=1.8 ③
②-①得:x-y=1 ④
③+④得:2x=2.8 ∴x=1.4
③-④得:2y=0.8 ∴y=0.4
∴原方程组的解是
当两个方程中未知数的系数恰好互换时,可以先把这两个方程分别相加、相减,达到求解的目的.
课堂练习
整体加减再认识
4x+4y=20
两个方程直接相加
x+y=5
两个方程直接相减
m-3n=-3
整体加减直接求值
课堂练习
三位同学分别提出了以下三种不同的解题思路:
课堂练习
解:①×2,得:4x+6y=8 ③
②×3,得:9x+6y=6m-9 ④
④-③,得:5x=6m-17
解得:x=
把x= 代入①得:
解得:
①
②
甲同学是直接根据方程组的解的概念先解方程组,得到用含m的式子表示x、y的表达式,再代入x-y=1得到关于m的方程,没有经过更多的观察和思考,解法比较繁琐,计算量大;
课堂练习
①
②
乙同学:先将方程组中的两个方程相减,再求m的值.
乙同学观察到了方程组中未知数x、y的系数,以及与x-y=1中的系数的特殊关系,利用整体代入简化计算,而且不用求出x、y的值就能解决问题,思路比较灵活,计算量小;
解:②-①,得:x-y=2m-7
∵x-y=1
∴2m-7=1
∴m=4
课堂练习
丙同学将三个方程做为一个整体,看成关于x,y的一次方程组,并且选择先解其中不含字母参数的x,y的二元一次方程组,相对计算量较小,但不如乙同学的简洁、灵活.
课堂练习
乙同学:先将方程组中的两个方程相加,再求m的值.
方法最佳,整体加减运用有条件限制.
方法相对繁琐,但是是解题的通法.
方法可行,重新组合也有条件限制.
学会观察思考,灵活解题,一题多解,选择最佳解题方法.
课堂练习
二元一次方程组
一元一次 方程
消元法
转化
代入消元法
加减消元法
整体代入
整体加减
整体思想
化繁为简
方程组的系数有绝对值为1
方程组的系数有绝对值相同,成倍数等
三元一次方程组
一元二次方程
消元
降次
整体思想
转化思想
一题多解
举一反三
课堂练习
课堂练习
课堂练习
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
