浙教版七年级下册数学 第一章 平行线 动点提高题(word版 无答案)
文档属性
| 名称 | 浙教版七年级下册数学 第一章 平行线 动点提高题(word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 408.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 15:26:45 | ||
图片预览




文档简介
2022年上半年春季 数学2022.02.26
相交线与平行线动点提高题
知识点:
1、平行线的判定:
①同位角相等,两直线平行。②内错角相等,两直线平行。 ③同旁内角互补,两直线平行。
2、推论:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
3、平行线的性质:
①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补。
4、平移:①平移前后的两个图形形状大小不变,位置改变。②对应点的线段平行且相等。
平移:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移平移变换,简称平移。
对应点:平移后得到的新图形中每一点,都是由原图形中的某一点移动后得到的,这样的两个点叫做对应点。
所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.
关键:动中求静.在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
>>>>>>>>>>>典型例题<<<<<<<<<
【例1】
(1)如图(1),EF⊥GF,垂足为F,∠AEF=150°,∠DGF=60°. 试判断AB和CD的位置关系,并说明理由.
(2)如图(2),AB∥DE,∠ABC=70°,∠CDE=147°,∠C=______.(直接给出答案)
(3)如图(3),CD∥BE,则∠2+∠3-∠1=______.(直接给出答案)
(4)如图(4),AB∥CD,∠ABE=∠DCF,求证:BE∥CF.
【例2】
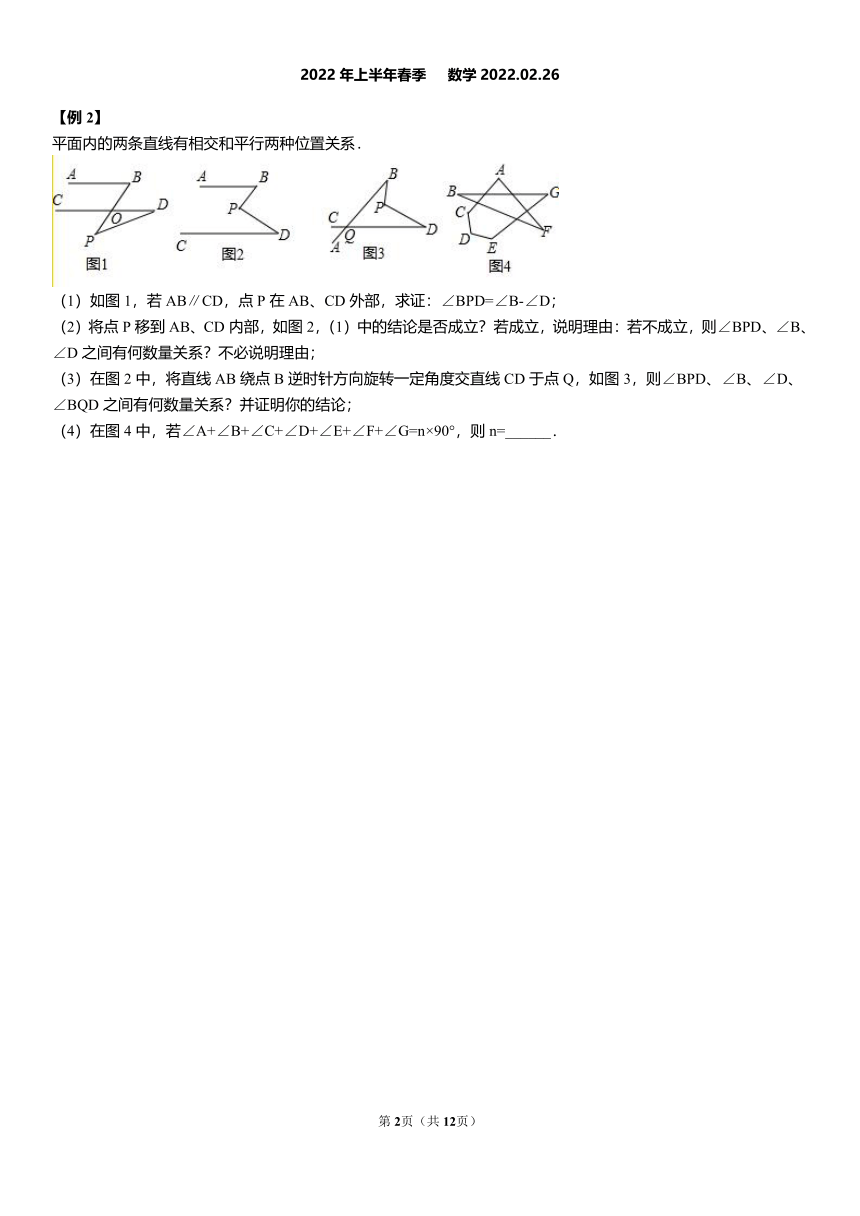
平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD外部,求证:∠BPD=∠B-∠D;
(2)将点P移到AB、CD内部,如图2,(1)中的结论是否成立?若成立,说明理由:若不成立,则∠BPD、∠B、∠D之间有何数量关系?不必说明理由;
(3)在图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;
(4)在图4中,若∠A+∠B+∠C+∠D+∠E+∠F+∠G=n×90°,则n=______.
【例3】
如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P落在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
>>>>>>>>>>>考点训练<<<<<<<<<<<<<
一.选择题
1.将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是( )
A.1 B.2 C.3 D.4
2.如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在射线OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是( )
A.60° B.80° C.100° D.120°
3.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
4.如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=( )
A.80° B.70° C.40° D.20°
5.如图,已知DE由线段AB平移得到的,且AB=DC=4cm,EC=3cm,则△DCE的周长是( )
A.9cm B.10cm C.11cm D.12cm
6.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16 cm B.18cm C.20cm D.22cm
二.填空题
1.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是___________________________________________________________.
2.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为___________度.
3.如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则△ACE的面积为________.
三.解答题
1.如图,已知,l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.
2.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数.
3.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=38°,则∠2=_________°,∠3=_________°.
(2)在(1)中,若∠1=55°,则∠3=_________°;若∠1=40°,则∠3=_________°.
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=_________°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
4.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
5.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
6.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
7.如图
(1)如图1,请证明∠A+∠B+∠C=180°
(2)如图2的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D
(3)如图3,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明
(4)如图4,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.
如图,在 △ABC 中,∠ACB=90°,AC=BC,AB=8cm ,过点C做射线 CD ,且CD//AB,点P从点C出发,沿射线 CD 方向均匀运动,速度为3cm/s ;同时,点Q从点A出发,沿 向点B匀速运动,速度为 1cm/s ,当点Q停止运动时,点P也停止运动.连接 PQ,CQ ,设运动时间为t(s) (0<t<8) .解答下列问题:
(1)用含有t的代数式表示CP 和BQ 的长度;
(2)当 t=2 时,请说明PQ//BC ;
(3)设△BCQ 的面积为S ,求S与t之间的关系式.
9.如图, AB//CD .
(1)如图①,若∠CMN=90° ,点B在射线MN上,∠ABM=120° ,求∠C的度数;
(2)如图②,若 ∠CMN=150° ,∠ABM - ∠C 是否为固定的度数?若是,写出这个度数,并说明理由;若不是,也请说明理由.
10.如图①,已知AB//CD, AC//EF
(1)若∠A=75°, ∠E=45°,求∠C和∠CDE的度数;
(2)探究:∠A、∠CDE与∠E之间有怎样的等量关系?并说明理由.
(3)若将图①变为图②,题设的条件不变,此时∠A、∠CDE 与∠E之间又有怎样的等量关系,请直接写出你探究的结论.
11.阅读下面材料:
(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关是 .
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
12.已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,求∠GMH的度数.
13.如图,点C,B分别在直线MN,PQ上,点A在直线MN,PQ之间,MN∥PQ.
(1)如图1,求证:∠A=∠MCA+∠PBA;
(2)如图2,过点C作CD∥AB,点E在PQ上,∠ECM=∠ACD,求证:∠A=∠ECN;
(3)在(2)的条件下,如图3,过点B作PQ的垂线交CE于点F,∠ABF的平分线交AC于点G,若∠DCE=∠ACE,∠CFB=∠CGB,求∠A的度数.
14.钱塘江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a、b的值;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图,两灯同时转动,在灯A射线到达AN之前,若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
15.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.
(1)(基础问题)如图1,试说明:∠AGD=∠A+∠D.
(2)(类比探究)如图2,当点G在线段EF延长线上时,直接写出∠AGD、∠A、∠D三者之间的数量关系.
(3)(应用拓展)如图3,AH平分∠GAB,DH交AH于点H,且∠GDH=2∠HDC,∠HDC=22°,∠H=32°,直接写出∠DGA的度数.
16.已知直线AB∥CD,
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM= ∠MBE,∠CDN= ∠NDE,直线MB、ND交于点F,则 = .
17.直线m与直线n相交于C,点A是直线m上一点,点B是直线n上一点, 的平分线 与 的平分线 的反向延长线相交于点P.
\
(1)如图1,若∠ACB=90° ,则∠P=___________;若 ∠ACB=α ,则∠P=___________(结果用含 α 的代数式表示);
(2)如图2,点F是直线n上一点,若点B在点C左侧,点F在点C右侧时,连接AF,∠CAF 与∠AFC 的平分线相交于点Q.
①随着点B、F的运动,∠APB+∠AQF 的值是否变化?若发生变化,请说明理由;若不发生变化,试求出其值;
②延长 交直线n于点G,作 交 于点H,则
A
B
①
②
③
④
A
B
①
②
③
④
A
B
①
②
③
④
P
(第5题图)
C
D
C
D
C
D
第35页(共35页)
相交线与平行线动点提高题
知识点:
1、平行线的判定:
①同位角相等,两直线平行。②内错角相等,两直线平行。 ③同旁内角互补,两直线平行。
2、推论:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
3、平行线的性质:
①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补。
4、平移:①平移前后的两个图形形状大小不变,位置改变。②对应点的线段平行且相等。
平移:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移平移变换,简称平移。
对应点:平移后得到的新图形中每一点,都是由原图形中的某一点移动后得到的,这样的两个点叫做对应点。
所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.
关键:动中求静.在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
>>>>>>>>>>>典型例题<<<<<<<<<
【例1】
(1)如图(1),EF⊥GF,垂足为F,∠AEF=150°,∠DGF=60°. 试判断AB和CD的位置关系,并说明理由.
(2)如图(2),AB∥DE,∠ABC=70°,∠CDE=147°,∠C=______.(直接给出答案)
(3)如图(3),CD∥BE,则∠2+∠3-∠1=______.(直接给出答案)
(4)如图(4),AB∥CD,∠ABE=∠DCF,求证:BE∥CF.
【例2】
平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD外部,求证:∠BPD=∠B-∠D;
(2)将点P移到AB、CD内部,如图2,(1)中的结论是否成立?若成立,说明理由:若不成立,则∠BPD、∠B、∠D之间有何数量关系?不必说明理由;
(3)在图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;
(4)在图4中,若∠A+∠B+∠C+∠D+∠E+∠F+∠G=n×90°,则n=______.
【例3】
如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角。(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)?
(3)当动点P落在第③部分时,全面探究∠PAC、∠APB、∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
>>>>>>>>>>>考点训练<<<<<<<<<<<<<
一.选择题
1.将一直角三角板与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是( )
A.1 B.2 C.3 D.4
2.如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=40°.在射线OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是( )
A.60° B.80° C.100° D.120°
3.如图,直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
4.如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=( )
A.80° B.70° C.40° D.20°
5.如图,已知DE由线段AB平移得到的,且AB=DC=4cm,EC=3cm,则△DCE的周长是( )
A.9cm B.10cm C.11cm D.12cm
6.如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A.16 cm B.18cm C.20cm D.22cm
二.填空题
1.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是___________________________________________________________.
2.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为___________度.
3.如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则△ACE的面积为________.
三.解答题
1.如图,已知,l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.
2.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数.
3.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=38°,则∠2=_________°,∠3=_________°.
(2)在(1)中,若∠1=55°,则∠3=_________°;若∠1=40°,则∠3=_________°.
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=_________°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
4.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
5.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
6.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
7.如图
(1)如图1,请证明∠A+∠B+∠C=180°
(2)如图2的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D
(3)如图3,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明
(4)如图4,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.
如图,在 △ABC 中,∠ACB=90°,AC=BC,AB=8cm ,过点C做射线 CD ,且CD//AB,点P从点C出发,沿射线 CD 方向均匀运动,速度为3cm/s ;同时,点Q从点A出发,沿 向点B匀速运动,速度为 1cm/s ,当点Q停止运动时,点P也停止运动.连接 PQ,CQ ,设运动时间为t(s) (0<t<8) .解答下列问题:
(1)用含有t的代数式表示CP 和BQ 的长度;
(2)当 t=2 时,请说明PQ//BC ;
(3)设△BCQ 的面积为S ,求S与t之间的关系式.
9.如图, AB//CD .
(1)如图①,若∠CMN=90° ,点B在射线MN上,∠ABM=120° ,求∠C的度数;
(2)如图②,若 ∠CMN=150° ,∠ABM - ∠C 是否为固定的度数?若是,写出这个度数,并说明理由;若不是,也请说明理由.
10.如图①,已知AB//CD, AC//EF
(1)若∠A=75°, ∠E=45°,求∠C和∠CDE的度数;
(2)探究:∠A、∠CDE与∠E之间有怎样的等量关系?并说明理由.
(3)若将图①变为图②,题设的条件不变,此时∠A、∠CDE 与∠E之间又有怎样的等量关系,请直接写出你探究的结论.
11.阅读下面材料:
(1)小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关是 .
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
12.已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,求∠GMH的度数.
13.如图,点C,B分别在直线MN,PQ上,点A在直线MN,PQ之间,MN∥PQ.
(1)如图1,求证:∠A=∠MCA+∠PBA;
(2)如图2,过点C作CD∥AB,点E在PQ上,∠ECM=∠ACD,求证:∠A=∠ECN;
(3)在(2)的条件下,如图3,过点B作PQ的垂线交CE于点F,∠ABF的平分线交AC于点G,若∠DCE=∠ACE,∠CFB=∠CGB,求∠A的度数.
14.钱塘江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a、b的值;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图,两灯同时转动,在灯A射线到达AN之前,若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
15.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.
(1)(基础问题)如图1,试说明:∠AGD=∠A+∠D.
(2)(类比探究)如图2,当点G在线段EF延长线上时,直接写出∠AGD、∠A、∠D三者之间的数量关系.
(3)(应用拓展)如图3,AH平分∠GAB,DH交AH于点H,且∠GDH=2∠HDC,∠HDC=22°,∠H=32°,直接写出∠DGA的度数.
16.已知直线AB∥CD,
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM= ∠MBE,∠CDN= ∠NDE,直线MB、ND交于点F,则 = .
17.直线m与直线n相交于C,点A是直线m上一点,点B是直线n上一点, 的平分线 与 的平分线 的反向延长线相交于点P.
\
(1)如图1,若∠ACB=90° ,则∠P=___________;若 ∠ACB=α ,则∠P=___________(结果用含 α 的代数式表示);
(2)如图2,点F是直线n上一点,若点B在点C左侧,点F在点C右侧时,连接AF,∠CAF 与∠AFC 的平分线相交于点Q.
①随着点B、F的运动,∠APB+∠AQF 的值是否变化?若发生变化,请说明理由;若不发生变化,试求出其值;
②延长 交直线n于点G,作 交 于点H,则
A
B
①
②
③
④
A
B
①
②
③
④
A
B
①
②
③
④
P
(第5题图)
C
D
C
D
C
D
第35页(共35页)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
