2021-2022学年浙教版七年级数学下册第1章平行线单元综合达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册第1章平行线单元综合达标测试题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 204.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览



文档简介
2021-2022学年浙教版七年级数学下册《第1章平行线》单元综合达标测试题(附答案)
一.选择题(共8小题,满分32分)
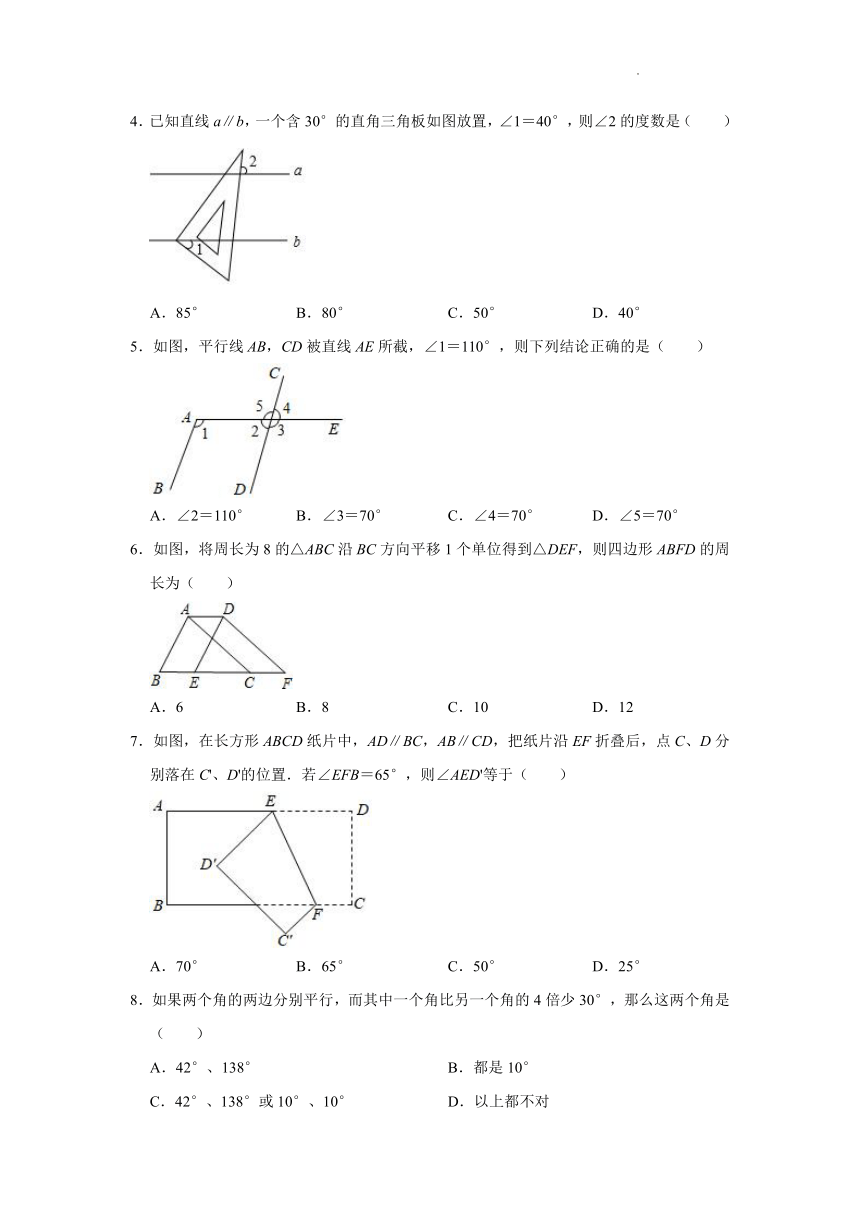
1.如图,下列判断中正确的个数是( )
(1)∠A与∠1是同位角;
(2)∠A和∠B是同旁内角;
(3)∠4和∠1是内错角;
(4)∠3和∠1是同位角.
A.1个 B.2个 C.3个 D.4个
2.如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;
(2)∠1=∠2;
(3)∠3=∠4;
(4)∠B=∠5.
A.1 B.2 C.3 D.4
3.如图,∠C+∠D=180°,∠DAE=3∠EBF,∠EBF=27°,点G是AB上的一点,若∠AGF=102°,∠BAF=34°,下列结论错误的是( )
A.∠AFB=81° B.∠E=54° C.AD∥BC D.BE∥FG
4.已知直线a∥b,一个含30°的直角三角板如图放置,∠1=40°,则∠2的度数是( )
A.85° B.80° C.50° D.40°
5.如图,平行线AB,CD被直线AE所截,∠1=110°,则下列结论正确的是( )
A.∠2=110° B.∠3=70° C.∠4=70° D.∠5=70°
6.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
7.如图,在长方形ABCD纸片中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C、D分别落在C'、D'的位置.若∠EFB=65°,则∠AED'等于( )
A.70° B.65° C.50° D.25°
8.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.42°、138° B.都是10°
C.42°、138°或10°、10° D.以上都不对
二.填空题(共8小题,满分32分)
9.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有 (只填序号).
10.如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:
①BC平分∠ABG;
②AC∥BG;
③与∠DBE互余的角有2个;
④若∠A=α,则∠BDF=180°﹣.
其中正确的是 .(请把正确结论的序号都填上)
11.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
12.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为 cm2.
13.如图,已知a∥b,∠2=95°,∠3=140°,则∠1的度数为 .
14.如图,AB∥DE,∠ABC=80°,∠CDE=150°,则∠BCD的度数为 °.
15.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=78°,∠DCE=120°,则∠E的度数是 .
16.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
三.解答题(共7小题,满分56分)
17.已知,∠1=72°,∠2=72°,∠3=108°.证明:AB∥EF,DE∥BC.
18.如图,已知AB∥CD,∠B=∠D,AE交BC的延长线于点E.
求证:AD∥BE.
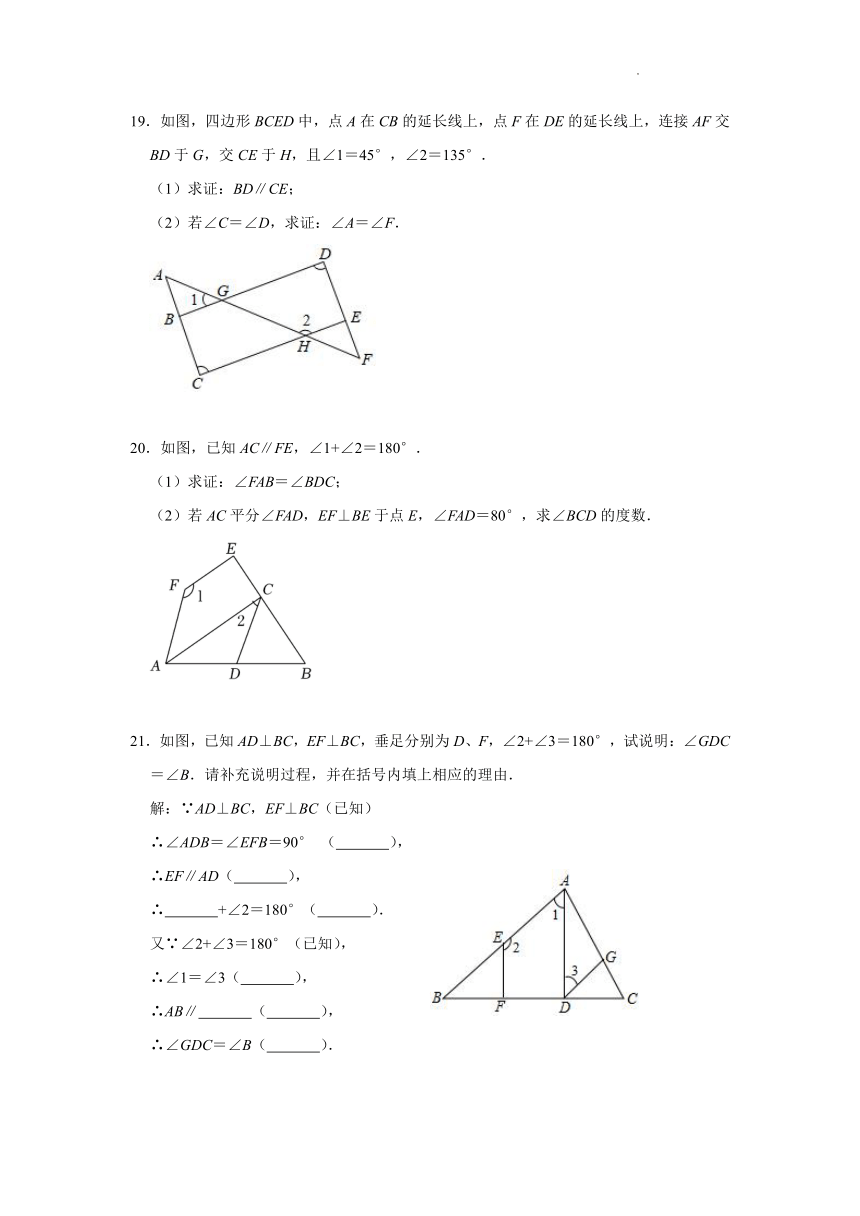
19.如图,四边形BCED中,点A在CB的延长线上,点F在DE的延长线上,连接AF交BD于G,交CE于H,且∠1=45°,∠2=135°.
(1)求证:BD∥CE;
(2)若∠C=∠D,求证:∠A=∠F.
20.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
21.如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( ),
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
22.(1)如图(1),AB∥EF.求证:∠BCF=∠B+∠F.
(2)当点C在直线BF的右侧时,如图(2),若AB∥EF,则∠BCF与∠B、∠F的关系如何?请说明理由.
23.已知AB∥CD,点E是AB,CD之间的一点.
(1)如图1,试探索∠AEC,∠BAE,∠DCE之间的数量关系;
以下是小明同学的探索过程,请你结合图形仔细阅读,并完成填空(理由或数学式):
解:过点E作PE∥AB(过直线外一点有且只有一条直线与这条直线平行).
∵AB∥CD(已知),
∴PE∥CD( ),
∴∠BAE=∠1,∠DCE=∠2( ),
∴∠BAE+∠DCE= + (等式的性质).
即∠AEC,∠BAE,∠DCE之间的数量关系是 .
(2)如图2,点F是AB,CD之间的一点,AF平分∠BAE,CF平分∠DCE.
①若∠AEC=74°,求∠AFC的大小;
②若CG⊥AF,垂足为点G,CE平分∠DCG,∠AEC+∠AFC=126°,求∠BAE的大小.
参考答案
一.选择题(共8小题,满分32分)
1.解:(1)∠A与∠1是同位角,正确;
(2)∠A与∠B是同旁内角.正确;
(3)∠4与∠1是内错角,正确;
(4)∠1与∠3不是同位角,错误.
故选:C.
2.解:(1)利用同旁内角互补,判定两直线平行,故(1)正确;
(2)利用内错角相等,判定两直线平行,∵∠1=∠2,∴AD∥BC,而不能判定AB∥CD,故(2)错误;
(3)利用内错角相等,判定两直线平行,故(3)正确;
(4)利用同位角相等,判定两直线平行,故(4)正确.
故选:C.
3.解:∵∠C+∠D=180°,
∴AD∥BC,故选项C正确,不符合题意;
∴∠DAE=∠CFE,
∵∠CFE=∠EBF+∠BEF,∠DAE=3∠EBF,∠EBF=27°,
∴∠CFE=3∠EBF=81°,∠BEF=54°,故选项B正确,不符合题意;
∴∠AFB=∠CFE=81°,故选项A正确,不符合题意;
∵∠AGF=102°,∠BAF=34°,
∴∠AFG=44°,
∵∠E=54°,
∴∠AFG≠∠E,
∴BE和FG不平行,故选项D错误,符合题意;故选:D.
4.解:如图,根据题意得∠3=60°,
∵∠1=40°,
∴∠4=∠1+∠3=40°+60°=100°,
∴∠5=180°﹣∠4=180°﹣100°=80°,
∵a∥b,
∴∠2=∠5=80°.
故选:B.
5.解:∵AB∥CD,∠1=110°,
∴∠5=∠3=110°,∠1+∠2=180°
∴∠4=∠2=70°,
即只有选项C答案正确.
故选:C.
6.解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
因为AD=1,BF=BC+CF=BC+1,DF=AC;
又因为AB+BC+AC=8,
所以,四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故选:C.
7.解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠DEF=∠EFB=65°,
又由折叠的性质可得∠D′EF=∠DEF=65°,
∴∠AED′=180°﹣65°﹣65°=50°,
故选:C.
8.解:如图1,∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2.
如图2,∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°
∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
设另一个角为x,则这一个角为4x﹣30°,
(1)两个角相等,则x=4x﹣30°,
解得x=10°,
4x﹣30°=4×10°﹣30°=10°;
(2)两个角互补,则x+(4x﹣30°)=180°,
解得x=42°,
4x﹣30°=4×42°﹣30°=138°.
所以这两个角是42°、138°或10°、10°.
故选:C.
二.填空题(共8小题,满分32分)
9.解:①用打气筒打气时,气筒里活塞的运动符合平移的定义,故正确;
②直线传送带上,瓶装饮料的移动符合平移的定义,故正确;
③在平直的公路上行驶的汽车符合平移的定义,故正确;
④随风摆动的旗帜不在同一条直线上,故错误;
⑤钟表的摆动不在同一条直线上,故错误;
故答案为:①②③.
10.解:∵CBD=90°,
∴∠ABC+∠EBD=90°,
又∵∠DBG=∠EBD,
∴∠ABC=∠CBG,
∴BC平分∠ABG,
∴①正确,
∵∠GBC=∠ABC=∠ACB,
∴AC∥BG,
∴②正确,
∵∠DBE=∠DBG,
∴与∠DBE互余的角有∠ABC,∠GBC,∠ACB,∠GCB,有4个,
∴③错误,
∵∠BDF=180°﹣∠BDG,∠BDG=90°﹣∠CBG=90°﹣∠ACB,
又∵∠ACB=×(180°﹣α)=90°﹣,
∴∠BDF=180°﹣[90°﹣(90°﹣)]=180°﹣,
∴④错误,
故答案为:①②.
11.解:延长直线,如图:,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
12.解:由题意,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故答案为:18.
13.解:∵∠3=140°,∠3+∠4=180°,
∴∠4=40°,
∵∠2=95°,∠2=∠5+∠4,
∴∠5=55°,
∵a∥b,
∴∠1+∠5=180°,
∴∠1=125°,
故答案为:125°.
14.解:如图,过点C作FG∥AB,
因为FG∥AB,AB∥DE,
所以 FG∥DE,
所以∠B=∠BCF,(两直线平行,内错角相等 )
∠CDE+∠DCF=180°,(两直线平行,同旁内角互补)
又因为∠B=80°,∠CDE=150°,
所以∠BCF=80°,(等量代换)
∠DCF=30°,(等式性质)
所以∠BCD=50°.
故答案为:50.
15.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=78°,
∴∠CFE=78°,
又∵∠DCE=120°,
∴∠E=∠DCE﹣∠CFE=120°﹣78°=42°.
故答案为:42°.
16.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
三.解答题(共7小题,满分56分)
17.证明:∵∠1=72°,∠2=72°(已知),
∴∠1=∠2(等量代换),
∴DE∥BC(内错角相等,两直线平行).
∵∠3=108°(已知),∠3+∠DGB=180°(邻补角定义),
∴∠DGB=180°﹣108°=72°.
∴∠DGB=∠2(等量代换).
∴AB∥EF(同位角相等,两直线平行).
∴AB∥EF,DE∥BC.
18.证明:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE.
19.证明:(1)∵∠CHG+∠2=180°,∠2=135°,
∴∠CHG=45°,
∵∠1=45°,
∴∠CHG=∠1,
∴BD∥CE.
(2)∵BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠ABD=∠D.
∴AC∥DF,
∴∠A=∠F.
20.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
21.解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD (同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B (两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
22.(1)证明:过C作CD∥AB,
∵AB∥EF,
∴CD∥AB∥EF,
∴∠B=∠BCD,∠F=∠FCD,
∴∠B+∠F=∠BCF.
(2)∠B+∠F+∠BCF=360°,
理由是:过C作CD∥AB,
则∠B+∠BCD=180°,
又∵AB∥EF,AB∥CD,
∴CD∥EF∥AB,
∴∠F+∠FCD=180°,
∴∠B+∠F+∠BCF=360°.
23.解:(1)平行于同一条直线的两条直线平行,
两直线平行,内错角相等,
∠1,∠2,
∠AEC=∠BAE+∠DCE,
故答案为:平行于同一条直线的两条直线平行,
两直线平行,内错角相等,
∠1,∠2,
∠AEC=∠BAE+∠DCE,
(2)①由(1)得:
∠AEC=∠BAE+∠DCE,
∠AFC=∠BAF+∠DCF,
∵AF平分∠BAE,CF平分∠DCE,
∴∠BAF=∠BAE,∠DCF=∠DCE,
∴∠AFC=∠BAF+∠DCF
=∠BAE+∠DCE
=∠AEC
=×74°
=37°;
②由①得:∠AEC=2∠AFC,
∵∠AEC+∠AFC=126°,
∴∠AFC=42°,∠AEC=82°,
∵CG⊥AF,
∴∠CGF=90°,
∴∠GCF=48°,
∵CE平分∠DCG,
∴∠GCE=∠ECD,
∵CF平分∠DCE,
∴∠DCE=2∠DCF=2∠ECF,
∴∠GCF=3∠DCF,
∴∠DCF=16°,
∴∠DCE=32°,
∴∠BAE=∠AEC﹣∠DCE=52°.
一.选择题(共8小题,满分32分)
1.如图,下列判断中正确的个数是( )
(1)∠A与∠1是同位角;
(2)∠A和∠B是同旁内角;
(3)∠4和∠1是内错角;
(4)∠3和∠1是同位角.
A.1个 B.2个 C.3个 D.4个
2.如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;
(2)∠1=∠2;
(3)∠3=∠4;
(4)∠B=∠5.
A.1 B.2 C.3 D.4
3.如图,∠C+∠D=180°,∠DAE=3∠EBF,∠EBF=27°,点G是AB上的一点,若∠AGF=102°,∠BAF=34°,下列结论错误的是( )
A.∠AFB=81° B.∠E=54° C.AD∥BC D.BE∥FG
4.已知直线a∥b,一个含30°的直角三角板如图放置,∠1=40°,则∠2的度数是( )
A.85° B.80° C.50° D.40°
5.如图,平行线AB,CD被直线AE所截,∠1=110°,则下列结论正确的是( )
A.∠2=110° B.∠3=70° C.∠4=70° D.∠5=70°
6.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
7.如图,在长方形ABCD纸片中,AD∥BC,AB∥CD,把纸片沿EF折叠后,点C、D分别落在C'、D'的位置.若∠EFB=65°,则∠AED'等于( )
A.70° B.65° C.50° D.25°
8.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.42°、138° B.都是10°
C.42°、138°或10°、10° D.以上都不对
二.填空题(共8小题,满分32分)
9.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送带上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有 (只填序号).
10.如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:
①BC平分∠ABG;
②AC∥BG;
③与∠DBE互余的角有2个;
④若∠A=α,则∠BDF=180°﹣.
其中正确的是 .(请把正确结论的序号都填上)
11.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
12.如图,将长为5cm,宽为3cm的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A'B'C'D',则阴影部分的面积为 cm2.
13.如图,已知a∥b,∠2=95°,∠3=140°,则∠1的度数为 .
14.如图,AB∥DE,∠ABC=80°,∠CDE=150°,则∠BCD的度数为 °.
15.某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题.如图所示,已知AB∥CD,∠BAE=78°,∠DCE=120°,则∠E的度数是 .
16.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=90°,则∠BFD= .
三.解答题(共7小题,满分56分)
17.已知,∠1=72°,∠2=72°,∠3=108°.证明:AB∥EF,DE∥BC.
18.如图,已知AB∥CD,∠B=∠D,AE交BC的延长线于点E.
求证:AD∥BE.
19.如图,四边形BCED中,点A在CB的延长线上,点F在DE的延长线上,连接AF交BD于G,交CE于H,且∠1=45°,∠2=135°.
(1)求证:BD∥CE;
(2)若∠C=∠D,求证:∠A=∠F.
20.如图,已知AC∥FE,∠1+∠2=180°.
(1)求证:∠FAB=∠BDC;
(2)若AC平分∠FAD,EF⊥BE于点E,∠FAD=80°,求∠BCD的度数.
21.如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( ),
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
22.(1)如图(1),AB∥EF.求证:∠BCF=∠B+∠F.
(2)当点C在直线BF的右侧时,如图(2),若AB∥EF,则∠BCF与∠B、∠F的关系如何?请说明理由.
23.已知AB∥CD,点E是AB,CD之间的一点.
(1)如图1,试探索∠AEC,∠BAE,∠DCE之间的数量关系;
以下是小明同学的探索过程,请你结合图形仔细阅读,并完成填空(理由或数学式):
解:过点E作PE∥AB(过直线外一点有且只有一条直线与这条直线平行).
∵AB∥CD(已知),
∴PE∥CD( ),
∴∠BAE=∠1,∠DCE=∠2( ),
∴∠BAE+∠DCE= + (等式的性质).
即∠AEC,∠BAE,∠DCE之间的数量关系是 .
(2)如图2,点F是AB,CD之间的一点,AF平分∠BAE,CF平分∠DCE.
①若∠AEC=74°,求∠AFC的大小;
②若CG⊥AF,垂足为点G,CE平分∠DCG,∠AEC+∠AFC=126°,求∠BAE的大小.
参考答案
一.选择题(共8小题,满分32分)
1.解:(1)∠A与∠1是同位角,正确;
(2)∠A与∠B是同旁内角.正确;
(3)∠4与∠1是内错角,正确;
(4)∠1与∠3不是同位角,错误.
故选:C.
2.解:(1)利用同旁内角互补,判定两直线平行,故(1)正确;
(2)利用内错角相等,判定两直线平行,∵∠1=∠2,∴AD∥BC,而不能判定AB∥CD,故(2)错误;
(3)利用内错角相等,判定两直线平行,故(3)正确;
(4)利用同位角相等,判定两直线平行,故(4)正确.
故选:C.
3.解:∵∠C+∠D=180°,
∴AD∥BC,故选项C正确,不符合题意;
∴∠DAE=∠CFE,
∵∠CFE=∠EBF+∠BEF,∠DAE=3∠EBF,∠EBF=27°,
∴∠CFE=3∠EBF=81°,∠BEF=54°,故选项B正确,不符合题意;
∴∠AFB=∠CFE=81°,故选项A正确,不符合题意;
∵∠AGF=102°,∠BAF=34°,
∴∠AFG=44°,
∵∠E=54°,
∴∠AFG≠∠E,
∴BE和FG不平行,故选项D错误,符合题意;故选:D.
4.解:如图,根据题意得∠3=60°,
∵∠1=40°,
∴∠4=∠1+∠3=40°+60°=100°,
∴∠5=180°﹣∠4=180°﹣100°=80°,
∵a∥b,
∴∠2=∠5=80°.
故选:B.
5.解:∵AB∥CD,∠1=110°,
∴∠5=∠3=110°,∠1+∠2=180°
∴∠4=∠2=70°,
即只有选项C答案正确.
故选:C.
6.解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
因为AD=1,BF=BC+CF=BC+1,DF=AC;
又因为AB+BC+AC=8,
所以,四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故选:C.
7.解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠DEF=∠EFB=65°,
又由折叠的性质可得∠D′EF=∠DEF=65°,
∴∠AED′=180°﹣65°﹣65°=50°,
故选:C.
8.解:如图1,∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2.
如图2,∵AB∥EF,
∴∠3+∠2=180°,
∵BC∥DE,
∴∠3=∠1,
∴∠1+∠2=180°
∴如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
设另一个角为x,则这一个角为4x﹣30°,
(1)两个角相等,则x=4x﹣30°,
解得x=10°,
4x﹣30°=4×10°﹣30°=10°;
(2)两个角互补,则x+(4x﹣30°)=180°,
解得x=42°,
4x﹣30°=4×42°﹣30°=138°.
所以这两个角是42°、138°或10°、10°.
故选:C.
二.填空题(共8小题,满分32分)
9.解:①用打气筒打气时,气筒里活塞的运动符合平移的定义,故正确;
②直线传送带上,瓶装饮料的移动符合平移的定义,故正确;
③在平直的公路上行驶的汽车符合平移的定义,故正确;
④随风摆动的旗帜不在同一条直线上,故错误;
⑤钟表的摆动不在同一条直线上,故错误;
故答案为:①②③.
10.解:∵CBD=90°,
∴∠ABC+∠EBD=90°,
又∵∠DBG=∠EBD,
∴∠ABC=∠CBG,
∴BC平分∠ABG,
∴①正确,
∵∠GBC=∠ABC=∠ACB,
∴AC∥BG,
∴②正确,
∵∠DBE=∠DBG,
∴与∠DBE互余的角有∠ABC,∠GBC,∠ACB,∠GCB,有4个,
∴③错误,
∵∠BDF=180°﹣∠BDG,∠BDG=90°﹣∠CBG=90°﹣∠ACB,
又∵∠ACB=×(180°﹣α)=90°﹣,
∴∠BDF=180°﹣[90°﹣(90°﹣)]=180°﹣,
∴④错误,
故答案为:①②.
11.解:延长直线,如图:,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
12.解:由题意,空白部分是矩形,长为5﹣2=3(cm),宽为3﹣1=2(cm),
∴阴影部分的面积=5×3×2﹣2×2×3=18(cm2),
故答案为:18.
13.解:∵∠3=140°,∠3+∠4=180°,
∴∠4=40°,
∵∠2=95°,∠2=∠5+∠4,
∴∠5=55°,
∵a∥b,
∴∠1+∠5=180°,
∴∠1=125°,
故答案为:125°.
14.解:如图,过点C作FG∥AB,
因为FG∥AB,AB∥DE,
所以 FG∥DE,
所以∠B=∠BCF,(两直线平行,内错角相等 )
∠CDE+∠DCF=180°,(两直线平行,同旁内角互补)
又因为∠B=80°,∠CDE=150°,
所以∠BCF=80°,(等量代换)
∠DCF=30°,(等式性质)
所以∠BCD=50°.
故答案为:50.
15.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=78°,
∴∠CFE=78°,
又∵∠DCE=120°,
∴∠E=∠DCE﹣∠CFE=120°﹣78°=42°.
故答案为:42°.
16.解:∵AB∥CD,
∴∠ABE=∠4,∠1=∠2,
∵∠BED=90°,∠BED=∠4+∠EDC,
∴∠ABE+∠EDC=90°,
∵BF平分∠ABE,DF平分∠CDE,
∴∠1+∠3=45°,
∵∠5=∠2+∠3,
∴∠5=∠1+∠3=45°,
即∠BFD=45°,
故答案为:45°.
三.解答题(共7小题,满分56分)
17.证明:∵∠1=72°,∠2=72°(已知),
∴∠1=∠2(等量代换),
∴DE∥BC(内错角相等,两直线平行).
∵∠3=108°(已知),∠3+∠DGB=180°(邻补角定义),
∴∠DGB=180°﹣108°=72°.
∴∠DGB=∠2(等量代换).
∴AB∥EF(同位角相等,两直线平行).
∴AB∥EF,DE∥BC.
18.证明:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE.
19.证明:(1)∵∠CHG+∠2=180°,∠2=135°,
∴∠CHG=45°,
∵∠1=45°,
∴∠CHG=∠1,
∴BD∥CE.
(2)∵BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠ABD=∠D.
∴AC∥DF,
∴∠A=∠F.
20.(1)证明:∵AC∥EF,
∴∠1+∠FAC=180°,
又∵∠1+∠2=180°,
∴∠FAC=∠2,
∴FA∥CD,
∴∠FAB=∠BDC;
(2)解:∵AC平分∠FAD,
∴∠FAC=∠CAD,∠FAD=2∠FAC,
由(1)知∠FAC=∠2,
∴∠FAD=2∠2,
∴∠2=∠FAD,
∵∠FAD=80°,
∴∠2=×80°=40°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠2=50°.
21.解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD (同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B (两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
22.(1)证明:过C作CD∥AB,
∵AB∥EF,
∴CD∥AB∥EF,
∴∠B=∠BCD,∠F=∠FCD,
∴∠B+∠F=∠BCF.
(2)∠B+∠F+∠BCF=360°,
理由是:过C作CD∥AB,
则∠B+∠BCD=180°,
又∵AB∥EF,AB∥CD,
∴CD∥EF∥AB,
∴∠F+∠FCD=180°,
∴∠B+∠F+∠BCF=360°.
23.解:(1)平行于同一条直线的两条直线平行,
两直线平行,内错角相等,
∠1,∠2,
∠AEC=∠BAE+∠DCE,
故答案为:平行于同一条直线的两条直线平行,
两直线平行,内错角相等,
∠1,∠2,
∠AEC=∠BAE+∠DCE,
(2)①由(1)得:
∠AEC=∠BAE+∠DCE,
∠AFC=∠BAF+∠DCF,
∵AF平分∠BAE,CF平分∠DCE,
∴∠BAF=∠BAE,∠DCF=∠DCE,
∴∠AFC=∠BAF+∠DCF
=∠BAE+∠DCE
=∠AEC
=×74°
=37°;
②由①得:∠AEC=2∠AFC,
∵∠AEC+∠AFC=126°,
∴∠AFC=42°,∠AEC=82°,
∵CG⊥AF,
∴∠CGF=90°,
∴∠GCF=48°,
∵CE平分∠DCG,
∴∠GCE=∠ECD,
∵CF平分∠DCE,
∴∠DCE=2∠DCF=2∠ECF,
∴∠GCF=3∠DCF,
∴∠DCF=16°,
∴∠DCE=32°,
∴∠BAE=∠AEC﹣∠DCE=52°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
