第1章 平行线单元自我综合评价（含答案）

中小学教育资源及组卷应用平台
第1章平行线自我综合评价
[范围:第1章　平行线　时间:40分钟　分值:100分]
一、选择题(每小题4分,共24分)
1.图1-Z-1中的哪一个图案可以看成是由图案自身的一部分经平移后得到的 (　　)
　　 A　　 　　B　　　　 C　　　　 D
图1-Z-1
2.如图1-Z-2所示,下列说法错误的是 (　　)
图1-Z-2
A.∠C与∠1是内错角 B.∠2与∠3是内错角
C.∠A与∠B是同旁内角 D.∠A与∠3是同位角
3.如图1-Z-3,下列条件中,能判定AB∥CD的是 (　　)
图1-Z-3
A.∠1=∠3 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
4.如图1-Z-4,BE平分∠DBC,A是BD上一点,过点A作AE∥BC交BE于点E,若∠DAE=56°,则∠E的度数为 (　　)
图1-Z-4
A.56° B.36° C.26° D.28°
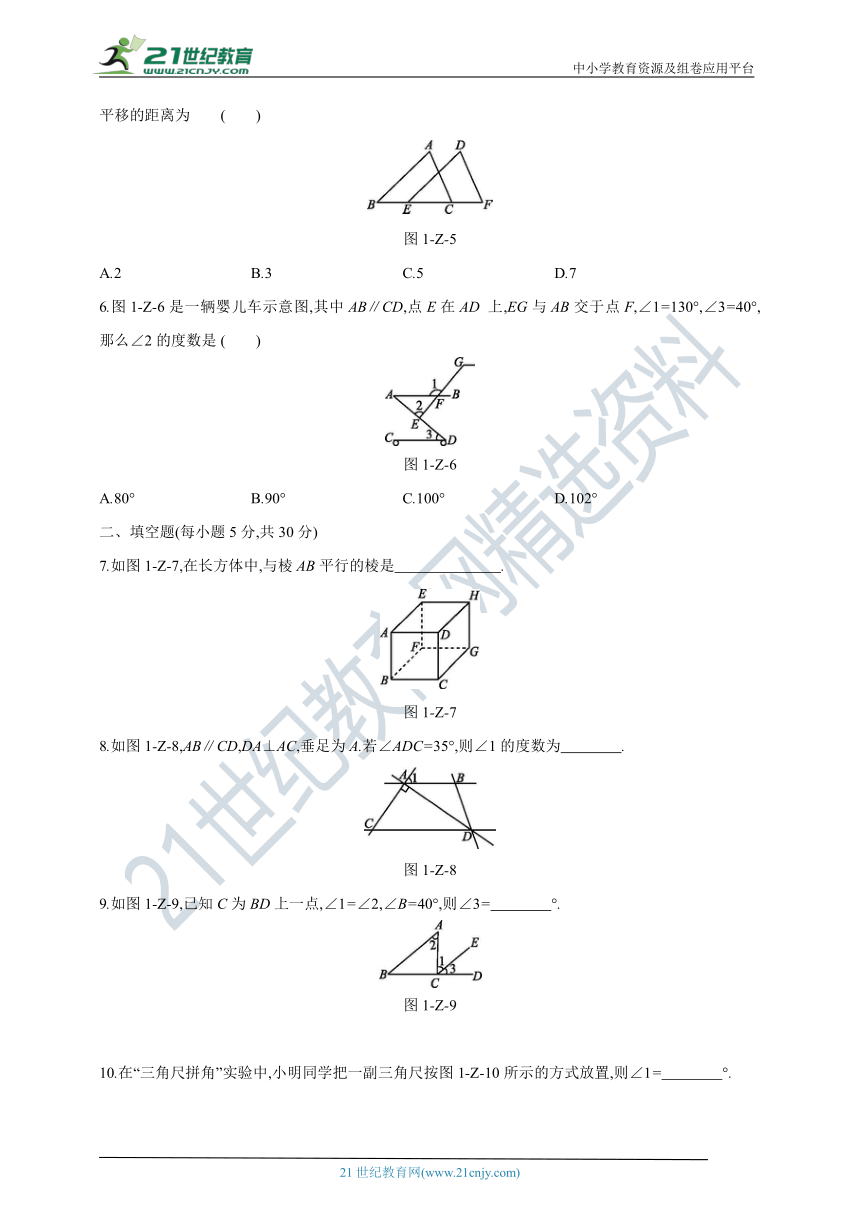
5.如图1-Z-5,三角形ABC沿着由点B到点C的方向平移到三角形DEF的位置.已知EF=5,EC=3,那么平移的距离为 (　　)
图1-Z-5
A.2 B.3 C.5 D.7
6.图1-Z-6是一辆婴儿车示意图,其中AB∥CD,点E在AD 上,EG与AB交于点F,∠1=130°,∠3=40°,那么∠2的度数是 (　　)
图1-Z-6
A.80° B.90° C.100° D.102°
二、填空题(每小题5分,共30分)
7.如图1-Z-7,在长方体中,与棱AB平行的棱是　　　　　　　.
图1-Z-7
8.如图1-Z-8,AB∥CD,DA⊥AC,垂足为A.若∠ADC=35°,则∠1的度数为　　　　.
图1-Z-8
9.如图1-Z-9,已知C为BD上一点,∠1=∠2,∠B=40°,则∠3=　　　　°.
图1-Z-9
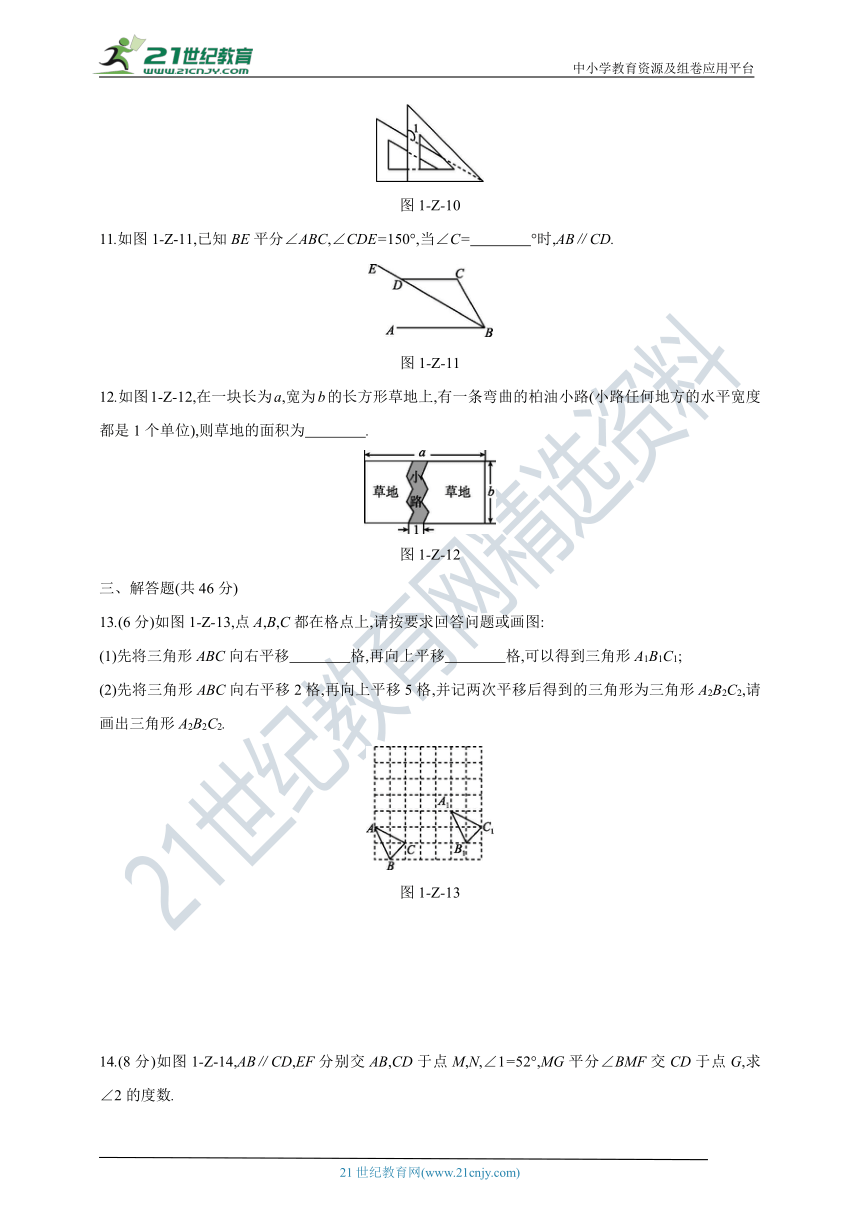
10.在“三角尺拼角”实验中,小明同学把一副三角尺按图1-Z-10所示的方式放置,则∠1=　　　　°.
图1-Z-10
11.如图1-Z-11,已知BE平分∠ABC,∠CDE=150°,当∠C=　　　　°时,AB∥CD.
图1-Z-11
12.如图1-Z-12,在一块长为a,宽为b的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),则草地的面积为　　　　.
图1-Z-12
三、解答题(共46分)
13.(6分)如图1-Z-13,点A,B,C都在格点上,请按要求回答问题或画图:
(1)先将三角形ABC向右平移　　　　格,再向上平移　　　　格,可以得到三角形A1B1C1;
(2)先将三角形ABC向右平移2格,再向上平移5格,并记两次平移后得到的三角形为三角形A2B2C2,请画出三角形A2B2C2.
图1-Z-13
14.(8分)如图1-Z-14,AB∥CD,EF分别交AB,CD于点M,N,∠1=52°,MG平分∠BMF交CD于点G,求∠2的度数.
图1-Z-14
解:∵∠1=52°(　　　　),
∴∠BMF=　　　　(　　　　　　　　).
∵MG平分∠　　　　,
∴∠BMG=　　　　=　　　　(　　　　　　　　).
∵AB∥CD(　　　　),∴∠2=　　　　=　　　　(　　　　　　　　　　　　　).
15.(10分)如图1-Z-15,点D,E分别在AB,AC上,DE∥BC,EF平分∠DEC,交BC于点F,且∠ABC=55°,∠C=70°.
(1)求∠DEF的度数;
(2)请判断EF与AB的位置关系,并说明理由.
图1-Z-15
16.(10分)如图1-Z-16所示,已知点D,E分别在AB,AC上,EF交BC于点F,DG交BC于点G,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.
图1-Z-16
17.(12分)如图1-Z-17,点D,E,F分别在AB,AC,BC上,∠1和∠2互补,∠C=∠EDF.
(1)DF与EC的位置关系为　;
(2)试判断DE与BC的位置关系,并说明理由;
(3)试判断∠DEC与∠CFD的大小关系,并说明理由.
图1-Z-17
详解详析
1.A　2.B　3.C　
4.D　[解析] ∵AE∥BC,∴∠E=∠EBC,∠DBC=∠DAE=56°.由角平分线的定义,得∠EBD=∠EBC=∠DBC,∴∠E=∠DBC=×56°=28°.故选D.
5.A　6.B
7.EF,HG,DC　8.55°
9.40　[解析] ∵∠1=∠2,
∴AB∥CE,
∴∠B=∠3.
∵∠B=40°,∴∠3=40°.
10.
120　[解析] 如图.因为∠B=∠DCF=90°,所以AB∥CD,所以∠A+∠AEC=180°.因为∠A=60°,所以∠AEC=120°.因为∠1=∠AEC,所以∠1=120°.
11.120
12.b(a-1)
13.(1)5　1　(2)略
14.已知　128°　邻补角的定义　BMF　∠BMF
64°　角平分线的定义　已知　∠BMG　64°　两直线平行,内错角相等
15.解:(1)∵DE∥BC,∠C=70°,
∴∠DEC=180°-∠C=110°.
又∵EF平分∠DEC,
∴∠DEF=∠DEC=55°.
(2)EF∥AB.理由:由(1)得∠DEF=55°.
又∵DE∥BC,
∴∠EFC=∠DEF=55°.
∵∠ABC=55°,
∴∠EFC=∠ABC,
∴EF∥AB.
16.解:∠AED=∠C.
理由:因为∠2+∠ADG=180°(平角的定义),
∠1+∠2=180°(已知),
所以∠1=∠ADG(同角的补角相等),
所以EF∥AB(同位角相等,两直线平行),
所以∠3=∠ADE(两直线平行,内错角相等).
又因为∠B=∠3(已知),
所以∠ADE=∠B(等量代换),
所以DE∥BC(同位角相等,两直线平行),
所以∠AED=∠C(两直线平行,同位角相等).
17.解:(1)DF∥EC
(2)DE∥BC.理由:
由(1)知DF∥EC,
∴∠C+∠CFD=180°.
又∵∠C=∠EDF,
∴∠EDF+∠CFD=180°,
∴DE∥CF,
即DE∥BC.
(3)∠DEC=∠CFD.理由:
由(2)知∠C+∠CFD=180°.
∵DE∥BC,
∴∠DEC+∠C=180°,
∴∠DEC=∠CFD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)