2.4二元一次方程组的应用 课件(共16张PPT)
文档属性
| 名称 | 2.4二元一次方程组的应用 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 16:40:12 | ||
图片预览






文档简介
(共16张PPT)
2.4二元一次方程组的应用
第2课时
浙教版 七年级下
例题讲解
例1. 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式l=pt+q计算.已测得当t =100℃时,l =2.002m;当t =500℃时,l=2.01m.
(1)求p,q的值;
解:(1)根据题意,得
100p+q=2.002 ①
500p+q=2.01 ②
p=0.00002
q=2
答:p=0.00002,q=2
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少
(2)由(1)得 l=0.00002t+2,当l=2.016时,
2.016=0.00002t+2,
解得 t=800.
答:这时金属棒的温度是800 ℃
这种求字母系数的方法称为待定系数法
课堂练习
声音在空气中传播的速度随着温度的变化而变化,科学家已测得一定温度下声音传播的速度如下表。如果用v表示声音在空气中的传播速度,t表示温度,则v,t满足公式:v=at+b(a,b为已知数),求a,b的值,并求当t=15℃时,v的值。
待定系数法
(1)代入
(2)列
(3)解
(4)回代
求代数式的值
例题讲解
例2.通过对一份中学生营养快餐的检测,得到以下信息:
① 快餐总质量为300 g;
② 快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
③ 蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%。
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比.
分析:(1)本题有哪些未知量?
(2)本题有哪些已知量?
蛋白质+碳水化合物+脂肪+矿物质=300g
蛋白质+脂肪=300 g × 50%
矿物质=2×脂肪
蛋白质+碳水化合物= 300 g × 85%
矿物质+碳水化合物= 300 g × 50%
例题讲解
蛋白质+脂肪=300g × 50%
矿物质+碳水化合物= 300g × 50%
矿物质=2×脂肪
蛋白质+碳水化合物= 300g × 85%
如何设元?
其他相关的未知量能用代数式来表示吗?
蛋白质+脂肪=300 g × 50%
矿物质+碳水化合物= 300g × 50%
{
设一份营养快餐中含蛋白质x g,脂肪y g,则矿物质为2y g,
碳水化合物为(300×85%-x)g.由题意,得
x=135
y=15
2y=2×15=30(g),
300×85%-x=255-135=120(g)
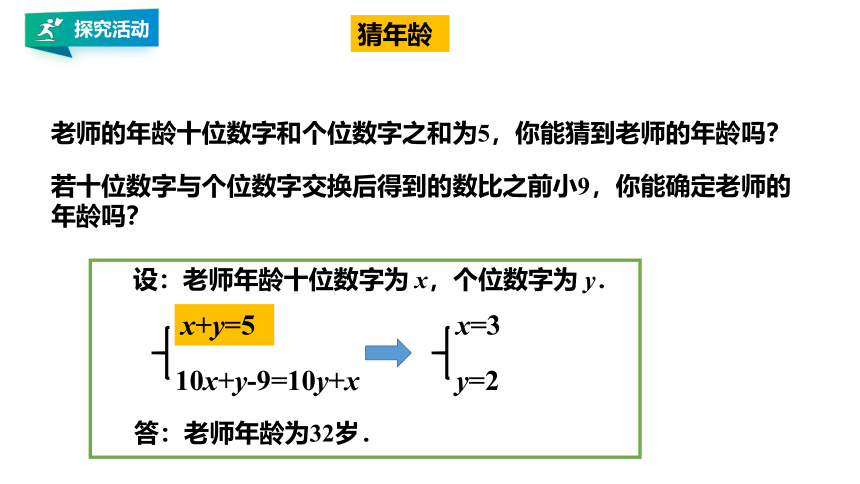
猜年龄
老师的年龄十位数字和个位数字之和为5,你能猜到老师的年龄吗?
十位数字 x 1 2 3 4 5
个位数字 y 4 3 2 1 0
老师年龄 10x+y 14 23 32 41 50
x+y=5
两位数的表示方式
探究活动
若十位数字与个位数字交换后得到的数比之前小9,你能确定老师的年龄吗?
x+y=5
10x+y-9=10y+x
x=3
y=2
设:老师年龄十位数字为 x,个位数字为 y.
答:老师年龄为32岁.
猜年龄
老师的年龄十位数字和个位数字之和为5,你能猜到老师的年龄吗?
探究活动
包子数
老师早上买了肉包、菜包共5个,肉包2元/个,菜包1.5元/个,共花了9元,但吃剩下1个包子.问:老师早上吃了肉包和菜包各几个?
肉包、菜包各买了几个?
设:老师买了 肉包 x 个,菜包 y 个.
x=3
y=2
肉包 2 3
菜包 2 1
x+y=5
2x+1.5y=9
∴老师买了3个肉包,2个菜包.
答:老师吃了2个肉包,2个菜包或3个肉包,1个菜包.
探究活动
植树节
有男生、女生共5人参加植树活动,男生挖坑,女生植树,男生每人每小时可以挖40个坑,女生每人每小时可以植树苗60棵,活动4小时后,女生刚好将男生挖的坑全部种上树苗.问:一共植树多少棵?
男生、女生各几人?
设:男生 x 人,女生 y 人.
x=3
y=2
坑 40×3×4=480
树 60×2×4=480
x+y=5
40x×4=60y×4
∴男生3人,女生2人.
答:一共植树480棵.
探究活动
去郊游
同学们去郊游,早上9点到达景点停车场,下车后先走一段平路,然后登山,到达山顶后游玩2小时按原路返回停车场.已知平路和山坡的路程之和为5km,同学们在平路上的平均速度是2.4km/h,上山的平均速度是2km/h,下山的平均速度是3km/h.问:同学们几点返回停车场?
设:平路 x km,山坡 y km.
x+y=5
?
x
y
t走=t平+t上坡+t下坡
∴9+2+ = .
∴同学们回到停车场的时间为15:10.
整体思想
探究活动
定方案
某企业急需采购某种产品6.2万件,计划租用小型卡车和大型卡车共5辆,准备一次运完.已知小型卡车每辆一次可运货1万件,大型卡车每辆一次可运货1.5万件.若小型卡车每辆租金100元,大型卡车每辆租金120元,请你设计最少租车费的方案.
设:租小型卡车 x 辆,大型卡车 y 辆.
x=2.6
y=2.4
小型x 1 2 3 4
大型y 4 3 2 1
x+1.5y 7 6.5 6 5.5
租金 580 560 540 520
x+y=5
x+1.5y=6.2
答:租小型卡车2辆,大型卡车3辆,租金最少为560元.
?
探究活动
买螃蟹
(a+b)x+(a+b)y=(a+b)(x+y)=75
x-y 1 3 7 21
a-b 21 7 3 1
x+y=5
答:买一只母蟹和一只公蟹需要15元.
老师今天准备买5只螃蟹,若买x只母蟹,y只公蟹,则一共48元,若买x只公蟹,y只母蟹,则一共27元.(市场上母蟹比公蟹贵)
(1)若买一只母蟹和一只公蟹需要多少钱?
(2)求x,y的值,及公蟹母蟹的单价.
螃蟹的单价?
设:母蟹 a 元/只,公蟹 b 元/只.
bx+ay=27
ax+by=48
a+b=15
(a-b)x+(b-a)y=(a-b)(x-y)=21
整数
整数
正数
正数
x-y=3
x+y=5
x=4
y=1
a-b=7
a+b=15
a=11
b=4
答:x=4,y=1,母蟹11元/只,公蟹4元/只.
×
×
×
探究活动
列方程解决实际问题的一般步骤:
设
列
解
验
答
直接
间接
二元一次方程
二元一次方程组
多解
唯一解
解的正确性
符合实际
注意:
列二元一次方程解决实际问题
唯一解
是否择优
整体思想
课堂总结
作业布置
作业本 2.4二元一次方程组的应用(2)
https://www.21cnjy.com/help/help_extract.php
2.4二元一次方程组的应用
第2课时
浙教版 七年级下
例题讲解
例1. 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式l=pt+q计算.已测得当t =100℃时,l =2.002m;当t =500℃时,l=2.01m.
(1)求p,q的值;
解:(1)根据题意,得
100p+q=2.002 ①
500p+q=2.01 ②
p=0.00002
q=2
答:p=0.00002,q=2
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少
(2)由(1)得 l=0.00002t+2,当l=2.016时,
2.016=0.00002t+2,
解得 t=800.
答:这时金属棒的温度是800 ℃
这种求字母系数的方法称为待定系数法
课堂练习
声音在空气中传播的速度随着温度的变化而变化,科学家已测得一定温度下声音传播的速度如下表。如果用v表示声音在空气中的传播速度,t表示温度,则v,t满足公式:v=at+b(a,b为已知数),求a,b的值,并求当t=15℃时,v的值。
待定系数法
(1)代入
(2)列
(3)解
(4)回代
求代数式的值
例题讲解
例2.通过对一份中学生营养快餐的检测,得到以下信息:
① 快餐总质量为300 g;
② 快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
③ 蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%。
试分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量和所占百分比.
分析:(1)本题有哪些未知量?
(2)本题有哪些已知量?
蛋白质+碳水化合物+脂肪+矿物质=300g
蛋白质+脂肪=300 g × 50%
矿物质=2×脂肪
蛋白质+碳水化合物= 300 g × 85%
矿物质+碳水化合物= 300 g × 50%
例题讲解
蛋白质+脂肪=300g × 50%
矿物质+碳水化合物= 300g × 50%
矿物质=2×脂肪
蛋白质+碳水化合物= 300g × 85%
如何设元?
其他相关的未知量能用代数式来表示吗?
蛋白质+脂肪=300 g × 50%
矿物质+碳水化合物= 300g × 50%
{
设一份营养快餐中含蛋白质x g,脂肪y g,则矿物质为2y g,
碳水化合物为(300×85%-x)g.由题意,得
x=135
y=15
2y=2×15=30(g),
300×85%-x=255-135=120(g)
猜年龄
老师的年龄十位数字和个位数字之和为5,你能猜到老师的年龄吗?
十位数字 x 1 2 3 4 5
个位数字 y 4 3 2 1 0
老师年龄 10x+y 14 23 32 41 50
x+y=5
两位数的表示方式
探究活动
若十位数字与个位数字交换后得到的数比之前小9,你能确定老师的年龄吗?
x+y=5
10x+y-9=10y+x
x=3
y=2
设:老师年龄十位数字为 x,个位数字为 y.
答:老师年龄为32岁.
猜年龄
老师的年龄十位数字和个位数字之和为5,你能猜到老师的年龄吗?
探究活动
包子数
老师早上买了肉包、菜包共5个,肉包2元/个,菜包1.5元/个,共花了9元,但吃剩下1个包子.问:老师早上吃了肉包和菜包各几个?
肉包、菜包各买了几个?
设:老师买了 肉包 x 个,菜包 y 个.
x=3
y=2
肉包 2 3
菜包 2 1
x+y=5
2x+1.5y=9
∴老师买了3个肉包,2个菜包.
答:老师吃了2个肉包,2个菜包或3个肉包,1个菜包.
探究活动
植树节
有男生、女生共5人参加植树活动,男生挖坑,女生植树,男生每人每小时可以挖40个坑,女生每人每小时可以植树苗60棵,活动4小时后,女生刚好将男生挖的坑全部种上树苗.问:一共植树多少棵?
男生、女生各几人?
设:男生 x 人,女生 y 人.
x=3
y=2
坑 40×3×4=480
树 60×2×4=480
x+y=5
40x×4=60y×4
∴男生3人,女生2人.
答:一共植树480棵.
探究活动
去郊游
同学们去郊游,早上9点到达景点停车场,下车后先走一段平路,然后登山,到达山顶后游玩2小时按原路返回停车场.已知平路和山坡的路程之和为5km,同学们在平路上的平均速度是2.4km/h,上山的平均速度是2km/h,下山的平均速度是3km/h.问:同学们几点返回停车场?
设:平路 x km,山坡 y km.
x+y=5
?
x
y
t走=t平+t上坡+t下坡
∴9+2+ = .
∴同学们回到停车场的时间为15:10.
整体思想
探究活动
定方案
某企业急需采购某种产品6.2万件,计划租用小型卡车和大型卡车共5辆,准备一次运完.已知小型卡车每辆一次可运货1万件,大型卡车每辆一次可运货1.5万件.若小型卡车每辆租金100元,大型卡车每辆租金120元,请你设计最少租车费的方案.
设:租小型卡车 x 辆,大型卡车 y 辆.
x=2.6
y=2.4
小型x 1 2 3 4
大型y 4 3 2 1
x+1.5y 7 6.5 6 5.5
租金 580 560 540 520
x+y=5
x+1.5y=6.2
答:租小型卡车2辆,大型卡车3辆,租金最少为560元.
?
探究活动
买螃蟹
(a+b)x+(a+b)y=(a+b)(x+y)=75
x-y 1 3 7 21
a-b 21 7 3 1
x+y=5
答:买一只母蟹和一只公蟹需要15元.
老师今天准备买5只螃蟹,若买x只母蟹,y只公蟹,则一共48元,若买x只公蟹,y只母蟹,则一共27元.(市场上母蟹比公蟹贵)
(1)若买一只母蟹和一只公蟹需要多少钱?
(2)求x,y的值,及公蟹母蟹的单价.
螃蟹的单价?
设:母蟹 a 元/只,公蟹 b 元/只.
bx+ay=27
ax+by=48
a+b=15
(a-b)x+(b-a)y=(a-b)(x-y)=21
整数
整数
正数
正数
x-y=3
x+y=5
x=4
y=1
a-b=7
a+b=15
a=11
b=4
答:x=4,y=1,母蟹11元/只,公蟹4元/只.
×
×
×
探究活动
列方程解决实际问题的一般步骤:
设
列
解
验
答
直接
间接
二元一次方程
二元一次方程组
多解
唯一解
解的正确性
符合实际
注意:
列二元一次方程解决实际问题
唯一解
是否择优
整体思想
课堂总结
作业布置
作业本 2.4二元一次方程组的应用(2)
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
