第2章二元一次方程组练习题2020-2021学年浙江省各地浙教版数学七年级下册期末试题选编(Word版含解析)
文档属性
| 名称 | 第2章二元一次方程组练习题2020-2021学年浙江省各地浙教版数学七年级下册期末试题选编(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 876.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-04 00:00:00 | ||
图片预览




文档简介
浙教版数学七年级下册第2章:二元一次方程组练习题
一、单选题
1.(2021·浙江宁波·七年级期末)若是关于的二元一次方程的一组解,则a的值为( )
A. B. C.2 D.7
2.(2021·浙江·七年级期末)下列方程中,是二元一次方程的是( )
A. B. C. D.
3.(2021·浙江·七年级期末)已知是方程的一个解,则a的值是( )
A.5 B.1 C. D.
4.(2021·浙江·七年级期末)下列四组数值是二元一次方程的解的是( )
A. B. C. D.
5.(2021·浙江·七年级期末)观察下列方程:(1);(2);(3);(4)其中二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
6.(2021·浙江柯桥·七年级期末)二元一次方程有无数多个解,下列四组值中是该方程的解的是( )
A. B. C. D.
7.(2021·浙江·七年级期末)已知是二元一次方程组的解,则m﹣n的值是( )
A.1 B.2 C.3 D.4
8.(2021·浙江·七年级期末)若关于x,y的方程组没有实数解,则( )
A.ab=-2
B.ab=-2且a≠1
C.ab≠-2
D.ab=-2且a≠2
9.(2021·浙江·七年级期末)关于x,y的方程组的解是,其中y的值被盖住了,不过仍能求出p,则p的值是( )
A.- B. C.- D.
10.(2021·浙江·七年级期末)已知关于x,y的方程组,其中﹣3≤a≤1,给出下列结论:①是方程组的解;②当a=﹣2时,x,y的值互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④若x≤1,则1≤y≤4.其中正确的是( )
A.①② B.②③ C.②③④ D.①③④
11.(2021·浙江·七年级期末)已知是二元一次方程2x-y=14的解,则k的值是( )
A.2 B.﹣2 C.3 D.﹣3
12.(2021·浙江·七年级期末)若方程组的解中x与y的值相等,则k为( )
A.4 B.3 C.2 D.1
13.(2021·浙江东阳·七年级期末)用加减消元法解二元一次方程组时,下列方法中无法消元的是( )
A.①×2﹣② B.②×(﹣3)﹣① C.①×(﹣2)+② D.①﹣②×3
14.(2021·浙江·七年级期末)用加减法解方程组下列解法错误的是( )
A.①×3-②×2,消去x B.①×2-②×3,消去y
C.①×(-3)+②×2,消去x D.①×2-②×(-3),消去y
15.(2021·浙江·七年级期末)已知是关于x,y的二元一次方程组的解,则a+b的值为( )
A.﹣5 B.﹣1 C.3 D.7
16.(2021·浙江·七年级期末)若是二元一次方程组的解,则x+2y的算术平方根为( )
A.3 B.3,-3 C. D.,-
17.(2021·浙江·七年级期末)方程组的解是( ).
A. B. C. D.
18.(2021·浙江·七年级期末)已知关于x、y的方程组得出下列结论,正确的是( )
①当时,方程组的解也是方程的解;②当时,;③不论a取什么实数,的值始终不变:④不存在a使得成立;
A.①②③ B.①②④ C.①③④ D.②③④
19.(2021·浙江·七年级期末)我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B. C. D.
20.(2021·浙江慈溪·七年级期末)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
21.(2021·浙江宁波·七年级期末)中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何 ”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. B. C. D.
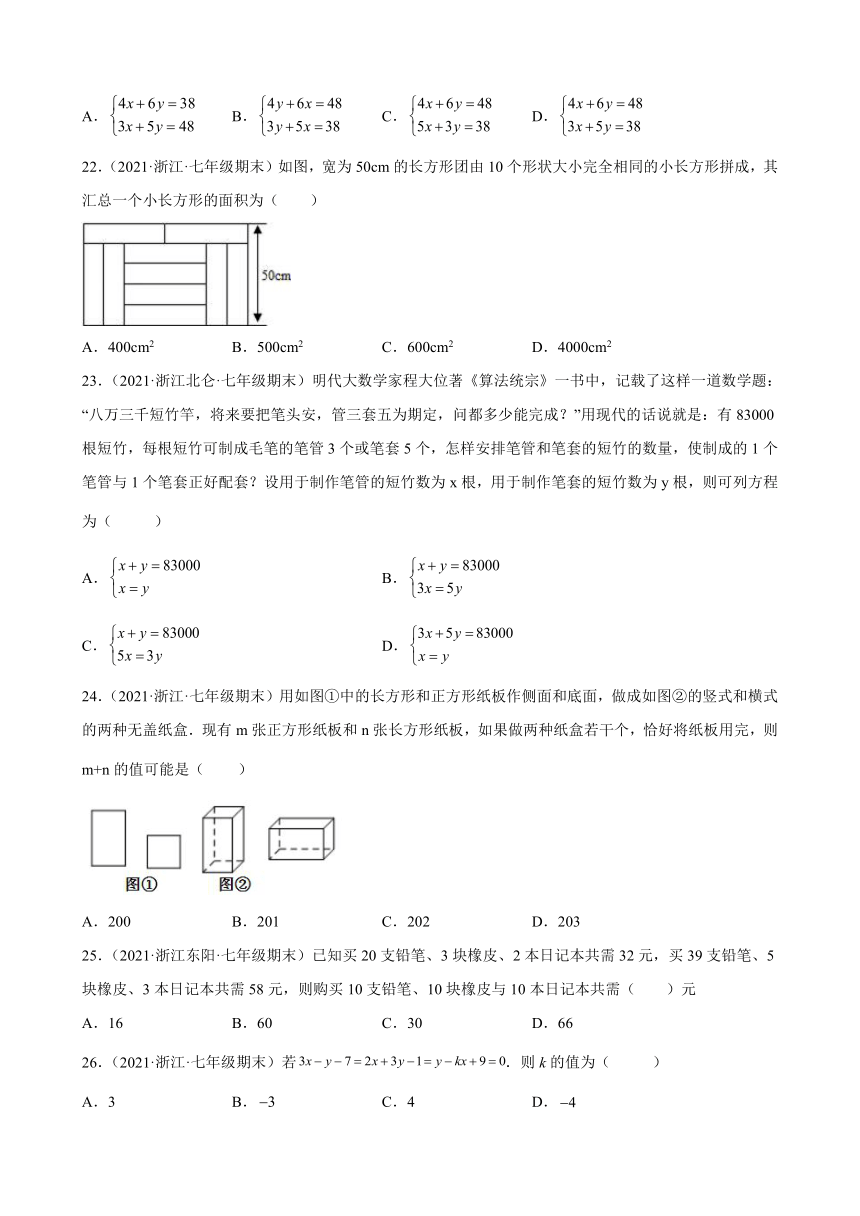
22.(2021·浙江·七年级期末)如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
A.400cm2 B.500cm2 C.600cm2 D.4000cm2
23.(2021·浙江北仑·七年级期末)明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问都多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )
A. B.
C. D.
24.(2021·浙江·七年级期末)用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.200 B.201 C.202 D.203
25.(2021·浙江东阳·七年级期末)已知买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买10支铅笔、10块橡皮与10本日记本共需( )元
A.16 B.60 C.30 D.66
26.(2021·浙江·七年级期末)若.则k的值为( )
A.3 B. C.4 D.
二、填空题
27.(2021·浙江海曙·七年级期末)已知a,b,c为3个自然数,满足,其中,则的最大值是__________.
28.(2021·浙江·七年级期末)若方程x|m|-2+(m+3)y2m-n=6是关于x、y的二元一次方程,则m+n=_____
29.(2021·浙江·七年级期末)若|a-b+1|与互为相反数,则a=____,b=____.
30.(2021·浙江·七年级期末)若关于,的方程是二元一次方程,则________ .
31.(2021·浙江·七年级期末)若是二元一次方程的解,则_________.
32.(2021·浙江·七年级期末)已知是方程mx+3y=1的一个解,则m的值是_______.
33.(2021·浙江·七年级期末)若是关于,的二元一次方程的一个解,则__________.
34.(2021·浙江·七年级期末)写出一个二元一次方程组是____________使它的解是.
35.(2021·浙江·七年级期末)已知二元一次方程组的解为,则_________.
36.(2021·浙江·杭州外国语学校七年级期末)若是的解,则满足的等量关系是__________.
37.(2021·浙江鄞州·七年级期末)将方程4x+3y=6变形成用y的代数式表示x,则x=________.
38.(2021·浙江柯桥·七年级期末)已知,则________.
39.(2021·浙江·七年级期末)如果实数m,n满足方程组,那么=______.
40.(2021·浙江·七年级期末)把方程(1﹣y)﹣x=0写成用含有x的式子表示y的形式,得y=____.
41.(2021·浙江越城·七年级期末)若方程组 的解是 ,则方程组 的解为__________________
42.(2021·浙江·七年级期末)已知关于x,y的二元一次方程组 的解互为相反数,则k的值是_________.
43.(2021·浙江·七年级期末)我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为__________尺,竿子长为__________尺.
44.(2021·浙江杭州·七年级期末)若关于x,y的二元一次方程组的解是正整数,则整数_______.
45.(2021·浙江·七年级期末)若方程组与方程组的解相同,则的值为______.
46.(2021·浙江·七年级期末)甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,若设甲的速度为x米/秒,乙的速度为y米/秒,可列方程组_____.
47.(2021·浙江·七年级期末)小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是__分钟.
48.(2021·浙江·杭州外国语学校七年级期末)有一片开心农场,蔬菜每天都在匀速生长,如果每天有20名游客摘菜,6天就能摘完;如果每天有17名游客摘菜,9天就能摘完(规定每名游客每天摘菜量相同),那么每天有14名游客摘菜,___天就能摘完.
49.(2021·浙江慈溪·七年级期末)学校设置了有关艺术类的甲、乙、丙三个拓展性课程项目,规定甲、乙两项不能兼报,学生选报后作了统计,发现报甲项目的人数与报乙项目的人数之和为报丙项目人数的;同时兼报甲、丙两项目的人数占报甲项目的人数的,同时兼报乙、丙两项目的人数占报乙项目的人数的;兼报甲、丙两项目的人数与兼报乙、丙两项目的人数之和是报丙项目人数的,则报甲、乙两个项目的人数之比为______.
50.(2021·浙江温岭·七年级期末)一个水池有,两个水口,其中为进水口,水口可进水也可出水(水口进出水速度相同).已知单独打开进水口,需要小时将水池由空池注满.若将,两个水口同时打开进水,小时将水池由空池注满;若将水口打开进水,同时水口打开出水,小时将水池由空池注满,则______.
51.(2021·浙江·七年级期末)对于实数x,y定义新运算其中a,b,c为常数,若,且有一个非零常数d,使得对于任意的x,恒有,则d的值是____.
三、解答题
52.(2021·浙江·杭州外国语学校七年级期末)解方程(组)
(1)
(2)
53.(2021·浙江柯桥·七年级期末)关于,的二元一次方程组与的解相同,求、的值.
54.(2021·浙江·七年级期末)解下列方程组:
(1)
(2)
55.(2021·浙江柯桥·七年级期末)解方程(组):
(1)
(2)
56.(2021·浙江·七年级期末)已知关于x、y的方程组 的解为 ,求m、n的值.
57.(2021·浙江·七年级期末)解方程组
(1)
(2)
58.(2021·浙江·七年级期末)解下列二元一次方程组:
(1)
(2)
59.(2021·浙江·七年级期末)解方程组:
(1)
(2)
60.(2021·浙江·七年级期末)(1)解方程组: (2)解方程组:
61.(2021·浙江·七年级期末)已知关于x,y的方程组
(1)请直接写出方程x+2y-6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
62.(2021·浙江·杭州外国语学校七年级期末)某中学为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元.
(1)求钢笔和毛笔的单价各为多少元?
(2)①学校仍需要购买上面的两种笔共105支(每种笔的单价不变).陈老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领2447元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.
②陈老师突然想起,所做的预算中还包括校长让他买的一支签字笔.如果签字笔的单价为小于10元的整数,请通过计算,直接写出签字笔的单价可能为 元.
63.(2021·浙江·七年级期末)亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
64.(2021·浙江·七年级期末)某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
65.(2021·浙江·七年级期末)海南五月瓜果飘香,某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
66.(2021·浙江·七年级期末)某景点的门票价格如下表:
购票人数(人) 1~50 51~99 100以上(含100)
门票单价(元) 48 45 42
(1)某校七年级1、2两个班共有102 人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737 元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
67.(2021·浙江·七年级期末)目前,新型冠状病毒在我国虽可控可防,但不可松懈.天府新区某校欲购置规格分别为300ml和500ml的甲、乙两种免洗手消毒液共300瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶.
(1)如果购买这两种消毒液共5550元,求甲、乙两种消毒液各购买多少瓶?
(2)在(1)的条件下,若该校在校师生共1320人,平均每人每天都需使用10ml的免洗手消毒液,则这批消毒液可使用多少天?
68.(2021·浙江温州·七年级期末)七年(1)(2)两班各40人参加垃圾分类知识竞赛,规则如图.比赛中,所有同学均按要求一对一连线,无多连、少连.
(1)分数5,10,15,20中,每人得分不可能是________分.
(2)七年(1)班有4人全错,其余成员中,满分人数是未满分人数的2倍;七年(2)班所有人都得分,最低分人数的2倍与其他未满分人数之和等于满分人数.
①问(1)班有多少人得满分?
②若(1)班除0分外,最低得分人数与其他未满分人数相等,问哪个班的总分高?
69.(2021·浙江·七年级期末)某大型超市投入15000元资金购进、两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价 成本价(元/箱) 销售价(元/箱)
A品牌 20 32
B品牌 35 50
(1)该大型超市购进、品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
70.(2021·浙江·七年级期末)为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.
(1)求医用口罩和洗手液的单价;
(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.
试卷第1页,共3页
参考答案:
1.A
【分析】
把代入方程,即可求解.
【详解】
∵是关于的二元一次方程的一组解,
∴,
∴a=-5,
故选:A
【点睛】
本题主要考查二元一次方程的解,掌握方程的解的定义,是解题的关键.
2.B
【分析】
二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【详解】
解:A、是二元二次方程,故此选项不符合;
B、是二元一次方程,故此选项符合;
C、是分式方程,故此选项不符合;
D、是二元二次方程,故此选项不符合;
故选B.
【点睛】
此题主要考查了二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
3.B
【分析】
将代入方程3x y=5得出关于a的方程,解之可得.
【详解】
将代入方程3x y=5,得:3a+2a=5,
解得:a=1,
故选B.
【点睛】
此题考查二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
4.B
【分析】
将各项中x与y的值代入方程检验即可.
【详解】
解:A、把代入方程得:左边=2-5=-3,右边=6,左边≠右边,不符合题意;
B、把代入方程得:左边=8-2=6,右边=6,左边=右边,符合题意;
C、把代入方程得:左边=4-4=0,右边=6,左边≠右边,不符合题意;
D、把代入方程得:左边=4-3=1,右边=6,左边≠右边,不符合题意;
故选:B.
【点睛】
此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
5.B
【分析】
根据二元一次方程的定义求解可得答案.
【详解】
解:(1),是二元一次方程;
(2),是二元一次方程;
(3),是一元二次方程;
(4),是一元一次方程;
故选:B.
【点睛】
本题考查了二元一次方程的定义,二元一次方程的定义是含有两个未知数且未知数的次数都为1.
6.B
【分析】
根据二元一次方程2x-y=1的解有无数个,所以此题应该用排除法确定答案,分别代入方程组,使方程左右相等的解才是方程组的解.
【详解】
解:A、把x=0,y=10.5代入方程,左边=-10.5≠1=右边,所以不符合题意;
B、把x=4,y=7代入方程,左边=1=右边,所以符合题意;
C、把x=1,y=11代入方程,左边=-9≠1=右边,所以不符合题意;
D、把x=15,y=11代入方程,左边=19≠1=右边,所以不符合题意.
故选:B.
【点睛】
本题考查了二元一次方程的解,要求理解什么是二元一次方程的解,并会把x,y的值代入原方程进行验证.
7.D
【分析】
根据已知将代入二元一次方程组得到m,n的值,即可求得m-n的值.
【详解】
∵是二元一次方程组
∴
∴m=1,n=-3
m-n=4
故选:D
【点睛】
本题考查了二元一次方程组解的定义,已知二元一次方程组的解,可求得方程组中的参数.
8.A
【分析】
把①变形,用y表示出x的值,再代入②得到关于y的方程,令y的系数等于0即可求出ab的值.
【详解】
,
由①得,x=-1-ay,
代入②得,b(-1-ay)-2y+a=0,
即(-ab-2)y=b-a,
因为此方程组没有实数根,所以b-a ≠0且-ab-2=0
解得ab=-2.
故选A.
【点睛】
考查的是解二元一次方程组,解答此类问题时要熟知解二元一次方程组的代入消元法和加减消元法.
9.A
【分析】
将x=1代入方程x+y=3求得y的值,将x、y的值代入x+py=0,可得关于p的方程,可求得p.
【详解】
解:根据题意,将x=1代入x+y=3,可得y=2,
将x=1,y=2代入x+py=0,得:1+2p=0,
解得:p=-,
故选:A.
【点睛】
本题主要考查二元一次方程组的解的概念,根据方程组的解会准确将方程的解代入是前提,严格遵循解方程的基本步骤求得方程的解是关键.
10.C
【详解】
①解方程组,
由②可知,代入①中,可得,
故方程组的解为,
∵,
∴,,
∴不是方程组的解,①错误.
②时,,,,互为相反数,②正确;
③时,,,满足,③正确;
④当时,,得,综合,在时,且.
∴,
∴,④正确.
故选.
点睛:本题考查了二元一次方程组的解,解一元一次不等式组.关键是根据条件,求出x、y的表达式及x、y的取值范围.
11.A
【分析】
根据方程的解的定义,将方程2x-y=14中x,y用k替换得到k的一元一次方程,进行求解.
【详解】
将代入二元一次方程2x-y=14,得
7k=14,
解得k=2.
故选A.
【点睛】
考查了二元一次方程的解的定义,只需把方程的解代入,进一步解一元一次方程即可.
12.C
【详解】
由题意得:x=y,
∴4x+3x=14,
∴x=2,y=2,
把它代入方程kx+(k-1)y=6得2k+2(k-1)=6,
解得k=2.
故选C.
13.D
【分析】
根据各选项分别计算,即可解答.
【详解】
方程组利用加减消元法变形即可.
解:A、①×2﹣②可以消元x,不符合题意;
B、②×(﹣3)﹣①可以消元y,不符合题意;
C、①×(﹣2)+②可以消元x,不符合题意;
D、①﹣②×3无法消元,符合题意.
故选:D.
【点睛】
本题考查了加减消元法解二元一次方程组,只有当两个二元一次方程未知数的系数相同或相反时才可以用加减法消元,系数相同相减消元,系数相反相加消元.
14.D
【详解】
本题考查了加减法解二元一次方程组
用加减法解二元一次方程组时,必须使同一未知数的系数相等或者互为相反数.如果系数相等,那么相减消元;如果系数互为相反数,那么相加消元.
A、,可消去x,故不合题意;
B、,可消去y,故不合题意;
C、,可消去x,故不合题意;
D、,得,不能消去y,符合题意.
故选D.
15.B
【分析】
将代入方程组,然后利用加减消元法解方程组,从而求解.
【详解】
解:∵是关于x,y的二元一次方程组的解
∴,解得:
∴a+b=-1
故选:B.
【点睛】
本题考查解二元一次方程组,掌握加减消元法解方程组的步骤和计算法则,正确计算是解题关键.
16.C
【分析】
将代入二元一次方程组中解出x和y的值,再计算x+2y的算术平方根即可.
【详解】
解:将代入二元一次方程中,
得到:,解这个关于x和y的二元一次方程组,
两式相加,解得,将回代方程中,解得,
∴,
∴x+2y的算术平方根为,
故选:C.
【点睛】
本题考查了二元一次方程组的解法,算术平方根的概念等,熟练掌握二元一次方程组的解法是解决本题的关键.
17.D
【分析】
采用加减消元法解方程组即可.
【详解】
①-②得:
∴
将代入①得:
∴
∴方程组的解为
故选D.
【点睛】
本题考查解二元一次方程组,熟练掌握消元法是解题的关键.
18.A
【分析】
①把a看做已知数表示出方程组的解,把a=0代入求出x与y的值,代入方程检验即可;②令x=y求出a的值,即可作出判断;③把x与y代入3x-y中计算得到结果,判断即可;④令2x=3y求出a的值,判断即可.
【详解】
解:,
①+②得:3x=3a-6,
解得:x=a-2,
把x=a-2代入①得:y=3a+3,
当a=0时,x=-2,y=3,
把x=-2,y=3代入x+y=1得:左边=-2+3=1,右边=1,是方程的解;
当x=y时,a-2=3a+3,即a=;
3x-y=3a-6-3a-3=-9,无论a为什么实数,3x-y的值始终不变,为-9;
令2x=3y,即2a-4=9a+9,即a=,存在,
则正确的结论是①②③,
故选A.
【点睛】
此题考查了二元一次方程组的解,二元一次方程的解,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.
19.A
【分析】
设索长为x尺,竿子长为y尺,根据“索比竿子长一托,折回索子却量竿,却比竿子短一托”,即可得出关于x、y的二元一次方程组.
【详解】
设索长为x尺,竿子长为y尺,
根据题意得:.
故选A.
【点睛】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
20.A
【分析】
根据“一根绳子去量一根木条,绳子剩余4.5尺”可知:绳子=木条+4.5,再根据“将绳子对折再量木条,木条剩余1尺”可知:绳子=木条-1,据此列出方程组即可.
【详解】
解:设木条长x尺,绳子长y尺,
那么可列方程组为:,
故选:A.
【点睛】
本题考查二元一次方程组的实际应用,解题的关键是明确题意,找出等量关系,列出相应的二元一次方程组.
21.D
【分析】
设马每匹x两,牛每头y两,根据“马四匹、牛六头,共价四十八两与马三匹、牛五头,共价三十八两列方程组即可.
【详解】
设马每匹x两,牛每头y两,由题意得
.
故选D.
【点睛】
本题考查了二元一次方程组的应用,仔细审题,找出题目的已知量和未知量,设两个未知数,并找出两个能代表题目数量关系的等量关系,然后列出方程组求解即可.
22.A
【分析】
设小长方形的长为xcm,小长方形的宽为ycm,根据图示,找出等量关系,列方程组求解.
【详解】
解:设小长方形的长为xcm,小长方形的宽为ycm,
由题意得,,
解得:,
小长方形的面积为:40×10=400(cm2).
故选A.
【点睛】
本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
23.B
【分析】
由用于生产笔管和笔套的短竹的数量结合生产的笔管总数=笔套的总数,即可得出关于x,y的二元一次方程组,此题得解.
【详解】
解:依题意,得:.
故选:B.
【点睛】
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
24.A
【分析】
分别设做了竖式无盖纸盒x个,横式无盖纸盒y个,列二元一次方程组,把两个方程的两边分别相加得,易知的值一定是5的倍数,本题即解答.
【详解】
解:设做成竖式无盖纸盒x个,横式无盖纸盒y个,根据题意列方程组得:
,
则两式相加得
,
∵x、y 都是正整数
∴一定是5的倍数;
∵200、201、202、203四个数中,只有200是5的倍数,
∴的值可能是200.
故选A.
【点睛】
本题主要考查二元一次方程组的实际应用;巧妙处理所列方程组,使两方程相加得出,是解答本题的关键.
25.B
【分析】
设铅笔单价为x元,橡皮的单价为y元,日记本的单价为z元,由题意:买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,列出方程组,求出x+y+z=6,即可求解.
【详解】
解:设铅笔单价为x元,橡皮的单价为y元,日记本的单价为z元,
由题意得:,
由①×2-②得:x+y+z=6,
∴10x+10y+10z=10×6=60,
即购买10支铅笔、10块橡皮与10本日记本共需60元,
故选:B.
【点睛】
本题考查了三元一次方程组的应用以及“整体思想”等知识;熟练掌握“整体思想”,找出等量关系列出方程组是解题的关键.
26.C
【分析】
先解出x、y的值,代入③,转化为关于k的方程来解.
【详解】
解:由题意可得,
①×3+②得11x-22=0,
解得x=2,
代入①得y=-1,
将x=2,y=-1代入③得,
-1-2k+9=0,
解得k=4.
故选:C.
【点睛】
本题实质是解三元一次方程组,先用了加减消元法求得x,y后,再求得k的值.
27.1346
【分析】
先化简绝对值,再根据方程取非负整数解即可.
【详解】
解:∵,
∴,
∵a,b,c为3个自然数,
要想取最大值,a应该取最小值0,
代入得,,
当b=1时,c最大,最大值为673,
,
故答案为:1346.
【点睛】
本题考查了绝对值化简和不定方程求非负整数解,解题关键是根据题意化简绝对值并确定a、b、c的最值.
28.8
【分析】
根据二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程可得|m|-2=1,2m-n=1,解出m、n的值可得答案.
【详解】
解:由题意,知|m|-2=1,2m-n=1且m+3≠0.
解得m=3,n=5.
所以m+n=3+5=8.
故答案是:8.
【点睛】
主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
29. -2, -1
【分析】
先根据互为相反数的和等于0列式,再根据非负数的性质列出二元一次方程组,最后解二元一次方程组求出、的值.
【详解】
与互为相反数,
,
,
② ①得,,
解得,
把代入①得,,
解得.
故答案为;.
【点睛】
本题考查了绝对值非负数,算术平方根非负数的性质,以及二元一次方程组的解法,根据几个非负数的和等于0,则每一个算术都等于0列式是解题的关键.
30.2或4
【分析】
根据二元一次方程的定义,可得x和y的指数分别都为1,列关于m、n的方程,然后求解即可.
【详解】
根据二元一次方程的定义:
解得:m=3,,
∴m+n=3+1=4或m+n=3-1=2;
故答案为:2或4.
【点睛】
本题考查二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程.
31.-1
【分析】
将x与y的值代入方程即可求出a的值.
【详解】
解:将x=3,y=1代入x+ay=2得:3+a=2,
解得:a=-1.
故答案为:-1.
【点睛】
此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
32.5
【分析】
直接将解代入方程即可求出m.
【详解】
把代入得, , .
【点睛】
本题考查方程的解的概念,给出方程的解,只需将解代入方程计算即可.
33.3
【分析】
根据二元一次方程的解定义,将x和y的值代入求解即可.
【详解】
由题意,将代入二元一次方程得:
解得
故答案为:3.
【点睛】
本题考查了二元一次方程的解定义,掌握解的定义是解题关键.
34.
【分析】
由1与-2列出两个算式,即可确定出所求方程组.
【详解】
解:根据题意得:,
故答案为:.
【点睛】
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
35.
【分析】
将代入计算即可.
【详解】
解:将代入,得
,
解得:,
∴,
故答案为:.
【点睛】
本题考查了二元一次方程组的解,将原方程的解代入原方程是解决本题的关键.
36.
【分析】
直接把代入方程组,然后消去c,即可得到答案.
【详解】
解:把代入方程组,得
,
由①×2:,③
由②+③:,
∴;
故答案为:.
【点睛】
本题考查了加减消元法解二元一次方程组,以及方程组的解,解题的关键是掌握加减消元法进行解题.
37.
【详解】
解:
4x=6-3y
x=
故答案为:.
38.4
【分析】
利用非负数的性质列出关于x与y的方程组,求出方程组的解得到x与y的值,即可求出所求式子的值.
【详解】
解:∵,
∴,
解得:,
∴4,
故答案为:4.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
39.1
【分析】
方程组中的两个方程相减可得,然后整体代入所求式子计算即可.
【详解】
解:对方程组,①-②,得,
所以.
故答案为:﹣1.
【点睛】
本题考查了二元一次方程组的解法和代数式求值,灵活应用整体的思想是解题的关键.
40.1﹣3x
【分析】
方程两边同乘以3后,再根据等式的性质进行变形即可求解.
【详解】
(1﹣y)﹣x=0,
1﹣y﹣3x=0,
即y=1﹣3x.
故答案为:1﹣3x.
【点睛】
本题考查了解二元一次方程,能正确根据等式的性质进行变形是解题的关键.
41.x=5.3,y=0.3
【分析】
通过观察两个方程组之间的关系,可得到,即可求解.
【详解】
方程组 的解是 ,
中,,
解得,
方程组的解为,
故答案为:x=5.3,y=0.3.
【点睛】
本题考查二元一次方程组的解,要比较两个方程组的结构相似处,得出是解题的关键.
42.-1
【详解】
∵关于x,y的二元一次方程组 的解互为相反数,
∴x=-y③,
把③代入②得:-y+2y=-1,
解得y=-1,所以x=1,
把x=1,y=-1代入①得2-3=k,
即k=-1.
故答案为-1
43. 20 15
【分析】
设索长为尺,竿子长为尺.根据题目中的等量关系列方程组求解即可.
【详解】
解:设索长为尺,竿子长为尺.根据题意得:
解得:
故答案为20,15.
【点评】
考查二元一次方程组的应用,解题的关键是找到题目中的等量关系.
44.0,3,4,5
【分析】
先解方程组,用m表示出方程组的解,根据方程组有正整数解得出m的值.
【详解】
解:
由②得:x=3y ③,
把③代入①得:6y my=6,
∴y=,
∴x=,
∵方程组的解是正整数,
∴6 m>0,
∴m<6,并且和是正整数,m是整数,
∴m的值为:0,3,4,5.
故答案是:0,3,4,5.
【点睛】
本题考查了二元一次方程组的解,一般情况下二元一次方程组的解是唯一的.数学概念是数学的基础与出发点,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.
45.2
【分析】
把代入方程组,得到一个关于a,b的方程组,将方程组的两个方程左右两边分别相加,整理即可得出a+b的值.
【详解】
解:把代入方程组,
得:,
①+②,得:7(a+b)=14,
则a+b=2.
故选:2.
【点睛】
此题主要考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.理解定义是关键.
46.
【分析】
根据题意,得出等量关系:①乙先跑10米,则甲跑5秒就可以追上乙;②乙先跑2秒,则甲跑4秒就可追上乙,得出方程组即可.
【详解】
解:根据乙先跑10米,则甲跑5秒就可以追上乙,得方程5x=5y+10;
根据乙先跑2秒,则甲跑4秒就可追上乙,得方程4x=4y+2y.
可得方程组.
故答案为:.
【点睛】
本题考查了二元一次方程组的应用,弄清题意,找准等量关系列出相应方程是解题的关键.
47.4
【分析】
设同向行驶的相邻两车的距离及车、小王的速度为未知数,等量关系为:6×车速-6×小王的速度=同向行驶的相邻两车的距离;3×车速+3×小王的速度=同向行驶的相邻两车的距离;把相关数值代入可得同向行驶的相邻两车的距离及车的速度关系式,相除可得所求时间.
【详解】
解:设18路公交车的速度是x米/分,小王行走的速度是y米/分,同向行驶的相邻两车的间距为s米.
每隔6分钟从背后开过一辆18路公交车,则6x-6y=s.①
每隔3分钟从迎面驶来一辆18路公交车,则3x+3y=s.②
由①,②可得s=4x,
∴.
故答案为:4.
即18路公交车总站发车间隔的时间是4分钟.
【点睛】
本题考查二元一次方程组的应用;根据追及问题和相遇问题得到两个等量关系是解决本题的关键;设出所需的多个未知数是解决本题的突破点.
48.18
【分析】
首先设原有蔬菜量为a,每天生长的蔬菜量为b,每名游客每天摘菜量为c,有14名游客摘菜x天就能摘完.根据“原蔬菜量+每天生长的蔬菜量×采摘天数=每名游客每天摘菜量×人数×天数”列出方程组,可解得x的值即为所求.
【详解】
解:首先设原有蔬菜量为a,每天生长的蔬菜量为b,每名游客每天摘菜量为c,有14名游客摘菜x天就能摘完,
依题意得 ,
由②﹣①得:
由③﹣②得:
将④代入⑤得:,
解得:
故答案是:18.
【点睛】
本题考查方程组的应用,有些应用题,它所涉及到的量比较多,量与量之间的关系也不明显,需增设一些表知数辅助建立方程,辅助表知数的引入,在已知条件与所求结论之间架起了一座“桥梁”,对这种辅助未知量,并不能或不需求出,可以在解题中相消或相约,这就是我们常说的“设而不求.”
49..
【分析】
设报甲项目的有x人,报乙项目的有y人,报丙项目的有z人,根据题意即可得出关于x,y,z的三元一次方程组,然后进一步化简即可得出答案;
【详解】
解:设报甲项目的有x人,报乙项目的有y人,报丙项目的有z人,
依题意得:
由①得:
将③代入②得:
化简得:
∴x:y=1:2.
故答案为:1:2.
【点睛】
本题考查了三元一次方程组的应用,找准等量关系,正确列出三元一次方程组是解题的关键.
50.
【分析】
设进水口速度为,进水口、出水口速度为,水池容量为,由题意,列出方程组求解即可.
【详解】
解:设进水口速度为,进水口、出水口速度为,水池容量为,
由题意得:,
由②③得:
,
解得:,
将代入①得:
,
解得:,
故答案为:.
【点睛】
本题考查了列方程组及求解,解题的关键是找准题中等量关系列出方程组即可.
51.4
【分析】
由新定义的运算,及,,构造方程组,不难得到参数,,之间的关系.又由有一个非零实数,使得对于任意实数,都有,可以得到一个关于的方程,解方程即可求出满足条件的的值.
【详解】
解:,
由,,即,
,.
又由对于任意实数恒成立,
,
为非零实数,
,
.
.
.
.
故答案为:4.
【点睛】
本题属于新定义的题目,根据新运算的定义,将已知中的数据代入进行运算是关键,同时考查了学生合情推理的能力,属于中档题.
52.(1);(2)
【分析】
(1)先利用分数的基本性质把方程化为:,再去分母,去括号,整理得:,从而可得答案;
(2)把视为整体未知数,先消去,求解 再求解 再求解即可得到答案.
【详解】
解:(1)
去分母得:
去括号得:
解得:
(2)
①×12得:,③
②+③得:
④
把代入②得:
⑤
④+⑤得:
把代入⑤得:
∴方程组的解为:
【点睛】
本题考查的是一元一次方程的解法,二元一次方程组的解法,根据方程的特点选择整体消元的解法是解题的关键.
53.,
【分析】
根据加减法,可得第二个方程组的解,根据方程组的解相同,可把第二个方程组的解代入第一个方程组,可得关于a、b的方程组,根据解方程组,可得答案.
【详解】
解:解得,
由的二元一次方程组与的解相同,得
,
①+②,得,
解得.
把代入①,得.解得.
【点睛】
本题考查了二元一次方程组的解,把方程组的解代入第一个方程组得出关于a、b的二元一次方程组是解题关键.
54.(1);(2)
【分析】
(1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【详解】
解:(1),
①+②得:6x=42,
解得:x=7,代入①中,
解得:y=9,
则方程组的解为;
(2)方程组化简为,
①+②得:3x=7,
解得:x=,代入①中,
解得:y=,
则方程组的解为.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
55.(1);(2)y=0
【分析】
(1)利用加减消元法求解可得.
(2)方程去分母,去括号,移项合并,把y系数化为1,即可求出解.
【详解】
解:(1),
①×3+②,得:5x=20,
解得:x=4,
将x=4代入①,得:4-y=2,
解得:y=2,
所以方程组的解为;
(2)去分母得:3y+6-4y+6=12,
移项合并得:-y=0,
解得:y=0.
【点睛】
此题考查了解一元一次方程,解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
56.m=1,n=1.
【详解】
试题分析:把x与y的值代入方程组得出关于的二元一次方程组,求得方程组的解即可.
试题解析:∵关于x、y的方程组 的解为
∴
解得:
即m=1,n=1.
57.(1);(2)
【分析】
(1)利用代入消元法求解即可;
(2)利用加减消元法求解即可;
【详解】
解:(1),
将②代入①中,得
3x-5(x+1)=3,
解得:x=-4,代入中②,
解得:y=-3,
∴原方程组的解为;
(2),
①×3+②×4得:
25x=50,解得:x=2,代入①中,
解得:y=1,
∴原方程组的解为.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
58.(1);(2)
【分析】
(1)令方程组的两个方程分别为①和②,将①代入②即可求得x的值,再将求得的x的值代入①可求得y的值;
(2)令方程组的两个方程分别为①和②,先化简②得到③,①×2得到④,④-③可求得y的值,将y值代入①,即可求得x的值;
【详解】
(1)
将①代入②,得7x=14
解得x=2
将x=2代入①,得y=8
∴方程组的解为:
故答案为:
(2)
由②,得③
①×2,得④
④-③,得13y=13
解得y=1
将y=1代入①,得2x=5
解得x=
故方程组的解为:
故答案为:
【点睛】
本题考查了二元一次方程组的解法,分别用到了代入消元法和加减消元法,代入消元法是将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入另一个方程中,消去一个未知数,得到一个一元一次方程,最后求得方程组的解;当方程中两个方程的某一未知数的系数相等或互为相反数时,把这两个方程的两边相加或相减来消去这个未知数,从而将二元一次方程化为一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法.
59.(1);(2).
【分析】
(1)利用代入消元法解二元一次方程组即可得;
(2)先通过去分母将方程组进行简单变形,再利用加减消元法解二元一次方程组即可得.
【详解】
(1),
将①代入②得:,
解得,
将代入②得:,
解得,
则方程组的解为;
(2)可变形为,
由①②得:,
解得,
将代入①得:,
解得,
则原方程组的解为.
【点睛】
本题考查了利用消元法解二元一次方程组,熟练掌握方程组的解法是解题关键.
60.(1);(2)
【分析】
(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【详解】
解:(1)把(1)代入(2)得:3(y+1)+y=7,
解得:y=1,
把y=1代入(1)得:x=1+1=2,
则方程组的解为;
(2)(2)×5-(1)×2得:21y=20,
解得:y=代入(2)得:2x+5×=8,
解得:x=,
则方程组的解为.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
61.(1), (2)m=(3)(4)
【分析】
(1)先对方程变形为x=6-2y,然后可带入数值求解;
(2)把已知的x+y=0和方程x+2y-6=0组合成方程组,求解方程组的解,然后代入方程x-2y+mx+5=0即可求m的值;
(3)方程整理后,根据无论m如何变化,二元一次方程组总有一个固定的解,列出方程组,解方程组即可;
(4)先把m当做已知求出x、y的值,然后再根据整数解进行判断即可.
【详解】
(1)
(2) 解得
把代入,解得m=
(3)
(4)
①+②得:
解得,
∵x恰为整数,m也为整数,
∴2+m=1或2+m=-1,
解得
62.(1) 钢笔的单价为21元,毛笔的单价为25元;(2)①见解析;②签字笔的单价可能为2元或6元.
【分析】
(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元.根据买钢笔30支,毛笔45支,共用了1755元建立方程,求出其解即可;
(2)①根据第一问的结论设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105 y)支,求出方程的解不是整数则说明算错了;
②设单价为21元的钢笔为z支,单价为25元的毛笔则为(105 y)支,签字笔的单价为a元,根据条件建立方程求出其解就可以得出结论.
【详解】
解:(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元.由题意得:
30x+45(x+4)=1755,
解得:x=21,
∴毛笔的单价为:x+4=25.
答:钢笔的单价为21元,毛笔的单价为25元.
(2)①设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105﹣y)支.根据题意,得
21y+25(105﹣y)=2447.
解之得:y=44.5 (不符合题意).
∴陈老师肯定搞错了.
②设单价为21元的钢笔为z支,签字笔的单价为a元,则根据题意,得
21z+25(105﹣z)=2447﹣a.
∴4z=178+a,
∵a、z都是整数,
∴178+a应被4整除,
∴a为偶数,又因为a为小于10元的整数,
∴a可能为2、4、6、8.
当a=2时,4z=180,z=45,符合题意;
当a=4时,4z=182,z=45.5,不符合题意;
当a=6时,4z=184,z=46,符合题意;
当a=8时,4z=186,z=46.5,不符合题意.
所以签字笔的单价可能2元或6元.
故答案为2元或6元.
【点睛】
本题考查了列二元一次方程组解实际问题的运用,列一元一次方程解实际问题的运用及二元一次不定方程的运用,在解答时根据题意等量关系建立方程是关键.
63.(1)计划36座的新能源客车6辆,共有218名志愿者;(2)调配36座新能源客车3辆,22座新能源客车5辆.
【分析】
(1)设计划调配36座新能源客车辆,该大学共有名志愿者.列方程组,得解方程组可得;(2)设调配36座新能源客车辆,22座新能源客车辆,根据题意,得,求正整数解;
【详解】
解:(1)设计划调配36座新能源客车辆,该大学共有名志愿者.
列方程组,得
解得
∴计划36座的新能源客车6辆,共有218名志愿者.
(2)设调配36座新能源客车辆,22座新能源客车辆,
根据题意,得,正整数解为
∴调配36座新能源客车3辆,22座新能源客车5辆.
【点睛】
考核知识点:二元一次方程组的运用.理解题意是关键.
64.(1)1辆小客车和1辆大客车都坐满后一次可送65名学生(2)租车方案有3种,①小客车20辆,大客车0辆;②小客车11辆,大客车4辆;③小客车2辆,大客车8辆(3)租小客车2辆,大客车8辆最省钱
【分析】
(1)设1辆小客车一次可送学生x人,1辆大客车都坐满后一次可送y名学生,根据题意可得等量关系:①用3辆小客车拉的人数+1辆大客车拉的人数=运送学生105人;②用1辆小客车拉的人数+2辆大客车拉的人数=运送学生110人,根据等量关系列出方程组,再解即可;
(2)设租小客车a辆,大客车b辆,由题意得:20×小客车的数量+45×大客车的数量=400人,根据等量关系列出方程,求出非负整数解即可;
(3)分别计算出每种租车方案的钱数,进行比较即可.
【详解】
(1)设1辆小客车一次可送学生x人,1辆大客车都坐满后一次可送y名学生,
由题意得:,
解得:,
所以x+y=65,
答:1辆小客车和1辆大客车都坐满后一次可送65名学生;
(2)设租小客车a辆,大客车b辆,由题意得:
20a+45b=400,可变形为,
∵每辆汽车恰好都坐满,
∴a、b的值均为非负整数,
∴a、b可取,,,
∴租车方案有3种,①小客车20辆,大客车0辆;②小客车11辆,大客车4辆;③小客车2辆,大客车8辆;
(3)各种租车费用:①20×200=4000(元);②11×200+4×380=3720(元);③2×200+8×380=3440(元);
∵3440<3720<4000,
∴租小客车2辆,大客车8辆最省钱
65.李叔叔购买“无核荔枝”12千克,购买“鸡蛋芒果”18千克..
【分析】
设李叔叔购买“无核荔枝”x千克,购买“鸡蛋芒果”y千克,根据总质量为30千克,总花费为708元,可得出方程组,解出即可.
【详解】
解:设李叔叔购买“无核荔枝” x千克,购买“鸡蛋芒果” y千克,
由题意,得:,解得:.
答:李叔叔购买“无核荔枝”12千克,购买“鸡蛋芒果”18千克.
66.(1)1班有49名学生,2班有53名学生;(2)八年级报名48人,九年级报名58人
【分析】
(1)设七年级1班有名学生,2班有名学生,由题意列出二元一次方程组,解方程组即可;
(2)设八年级报名人,九年级报名人,分两种情况:①若,②若,由题意分别列出方程组,解方程组即可.
【详解】
解:(1)设七年级1班有x名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1班有49名学生,2班有53名学生;
(2)设八年级报名x人,九年级报名y人,
分两种情况:
①若,
由题意得:,
解得:,(不合题意舍去);
②若,
由题意得:,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.
【点睛】
本题主要考查了二元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.注意(2)要分两种情况作答.
67.(1)甲种消毒液购买90瓶,乙种消毒液购买210瓶;(2)这批消毒液可使用10天
【分析】
(1)设甲种消毒液购买x瓶,乙种消毒液购买y瓶,由甲、乙两种免洗手消毒液共300瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶,列出方程组,即可求解;
(2)设这批消毒液可使用a天,由该校在校师生共1320人,平均每人每天都需使用10ml的免洗手消毒液,列出方程可求解.
【详解】
解:(1)设甲种消毒液购买x瓶,乙种消毒液购买y瓶,
由题意可得:,
解得:,
答:甲种消毒液购买90瓶,乙种消毒液购买210瓶;
(2)设这批消毒液可使用a天,
由题意可得:1320×10×a=90×300+500×210,
解得:a=10,
答:这批消毒液可使用10天.
【点睛】
本题考查了二元一次方程组的应用,一元一次方程的应用,根据题意列出方程和方程组是解答本题的关键.
68.(1)15;(2)①七年级(1)班有24人得满分;②七年级(2)班的总分高.
【分析】
(1)分别对连正确的数量进行分析,即可得到答案;
(2)①设七年(1)班满分人数有x人,则未满分的有人,然后列出方程,解方程即可得到答案;
②根据题意,先求出两个班各分数段的人数,然后求出各班的总分,即可进行比较.
【详解】
解:(1)根据题意,
连对0个得分为0分;
连对一个得分为5分;
连对两个得分为10分;
连对四个得分为20分;
不存在连对三个的情况,则得15分是不可能的;
故答案为:15.
(2)①根据题意,
设七年(1)班满分人数有x人,则未满分的有人,则
,
解得:,
∴(1)班有24人得满分;
②根据题意,(1)班中除0分外,最低得分人数与其他未满分人数相等,
∴(1)班得5分和10分的人数相等,
人数为:(人);
∴(1)班得总分为:(分);
由题意,(2)班存在得5分、得10分、得20分,三种情况,
设得5分的有y人,得10分的有z人,满分20分的有人,
∴,
∴,
∴七(2)班得总分为:
(分);
∵,
∴七(2)班的总分高.
【点睛】
本题考查了二元一次方程的应用,一元一次方程的应用,解题的关键是熟练掌握题意,正确掌握题目的等量关系,列出方程进行解题.
69.(1)该超市进品牌矿泉水400箱,品牌矿泉水200箱;(2)该超市共获利润7800元.
【分析】
(1)设该超市进A品牌矿泉水x箱,B品牌矿泉水y箱,“购进、两种品牌的矿泉水共600箱”和“投入15000元资金”,可列二元一次方程组,求解即可;
(2)根据 “总利润=A品牌矿泉水每箱利润×数量+ B品牌矿泉水每箱利润×数量”,即可求出该超市销售完600箱矿泉水获得的利润.
【详解】
解:(1)设该超市进品牌矿泉水箱,品牌矿泉水箱,
依题意,得:,
解得:.
答:该超市进品牌矿泉水400箱,品牌矿泉水200箱.
(2)(元)
答:该超市共获利润7800元.
【点睛】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
70.(1)医用口罩的单价为2.5元/个,洗手液的单价为30元/瓶;(2)有3种购买方案,方程见解析
【分析】
(1)设医用口罩的单价为x元/个,洗手液的单价为y元/瓶,根据题意列出二元一次方程组,解方程组即可;
(2)设增加购买N95口罩a个,洗手液b瓶,则医用口罩(1200-a)个,根据题意列出方程,将b用a表示出来,根据a,b都为正整数,得出满足题意的a,b的值.
【详解】
(1)设医用口罩的单价为x元/个,洗手液的单价为y元/瓶,根据题意得
解得
∴医用口罩的单价为2.5元/个,洗手液的单价为30元/瓶.
故答案为:医用口罩的单价为2.5元/个,洗手液的单价为30元/瓶
(2)设增加购买N95口罩a个,洗手液b瓶,则医用口罩(1200-a)个,根据题意得
6a+2.5(1200-a)+30b=5400
化简,得7a+60b=4800
∴b=80-
∵a,b都为正整数
∴a为60的倍数,且a≤200
∴,,
∴有三种购买方案
故答案为:有3种购买方案,方程见解析
【点睛】
本题考查了二元一次方程组的应用,先找到题中未知量,根据题中的等量关系,列出方程,解方程,对方程的解进行检验,舍去不符合题意的解.
答案第1页,共2页
一、单选题
1.(2021·浙江宁波·七年级期末)若是关于的二元一次方程的一组解,则a的值为( )
A. B. C.2 D.7
2.(2021·浙江·七年级期末)下列方程中,是二元一次方程的是( )
A. B. C. D.
3.(2021·浙江·七年级期末)已知是方程的一个解,则a的值是( )
A.5 B.1 C. D.
4.(2021·浙江·七年级期末)下列四组数值是二元一次方程的解的是( )
A. B. C. D.
5.(2021·浙江·七年级期末)观察下列方程:(1);(2);(3);(4)其中二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
6.(2021·浙江柯桥·七年级期末)二元一次方程有无数多个解,下列四组值中是该方程的解的是( )
A. B. C. D.
7.(2021·浙江·七年级期末)已知是二元一次方程组的解,则m﹣n的值是( )
A.1 B.2 C.3 D.4
8.(2021·浙江·七年级期末)若关于x,y的方程组没有实数解,则( )
A.ab=-2
B.ab=-2且a≠1
C.ab≠-2
D.ab=-2且a≠2
9.(2021·浙江·七年级期末)关于x,y的方程组的解是,其中y的值被盖住了,不过仍能求出p,则p的值是( )
A.- B. C.- D.
10.(2021·浙江·七年级期末)已知关于x,y的方程组,其中﹣3≤a≤1,给出下列结论:①是方程组的解;②当a=﹣2时,x,y的值互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④若x≤1,则1≤y≤4.其中正确的是( )
A.①② B.②③ C.②③④ D.①③④
11.(2021·浙江·七年级期末)已知是二元一次方程2x-y=14的解,则k的值是( )
A.2 B.﹣2 C.3 D.﹣3
12.(2021·浙江·七年级期末)若方程组的解中x与y的值相等,则k为( )
A.4 B.3 C.2 D.1
13.(2021·浙江东阳·七年级期末)用加减消元法解二元一次方程组时,下列方法中无法消元的是( )
A.①×2﹣② B.②×(﹣3)﹣① C.①×(﹣2)+② D.①﹣②×3
14.(2021·浙江·七年级期末)用加减法解方程组下列解法错误的是( )
A.①×3-②×2,消去x B.①×2-②×3,消去y
C.①×(-3)+②×2,消去x D.①×2-②×(-3),消去y
15.(2021·浙江·七年级期末)已知是关于x,y的二元一次方程组的解,则a+b的值为( )
A.﹣5 B.﹣1 C.3 D.7
16.(2021·浙江·七年级期末)若是二元一次方程组的解,则x+2y的算术平方根为( )
A.3 B.3,-3 C. D.,-
17.(2021·浙江·七年级期末)方程组的解是( ).
A. B. C. D.
18.(2021·浙江·七年级期末)已知关于x、y的方程组得出下列结论,正确的是( )
①当时,方程组的解也是方程的解;②当时,;③不论a取什么实数,的值始终不变:④不存在a使得成立;
A.①②③ B.①②④ C.①③④ D.②③④
19.(2021·浙江·七年级期末)我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B. C. D.
20.(2021·浙江慈溪·七年级期末)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
A. B.
C. D.
21.(2021·浙江宁波·七年级期末)中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何 ”设马每匹x两,牛每头y两,根据题意可列方程组为( )
A. B. C. D.
22.(2021·浙江·七年级期末)如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
A.400cm2 B.500cm2 C.600cm2 D.4000cm2
23.(2021·浙江北仑·七年级期末)明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问都多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )
A. B.
C. D.
24.(2021·浙江·七年级期末)用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.200 B.201 C.202 D.203
25.(2021·浙江东阳·七年级期末)已知买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买10支铅笔、10块橡皮与10本日记本共需( )元
A.16 B.60 C.30 D.66
26.(2021·浙江·七年级期末)若.则k的值为( )
A.3 B. C.4 D.
二、填空题
27.(2021·浙江海曙·七年级期末)已知a,b,c为3个自然数,满足,其中,则的最大值是__________.
28.(2021·浙江·七年级期末)若方程x|m|-2+(m+3)y2m-n=6是关于x、y的二元一次方程,则m+n=_____
29.(2021·浙江·七年级期末)若|a-b+1|与互为相反数,则a=____,b=____.
30.(2021·浙江·七年级期末)若关于,的方程是二元一次方程,则________ .
31.(2021·浙江·七年级期末)若是二元一次方程的解,则_________.
32.(2021·浙江·七年级期末)已知是方程mx+3y=1的一个解,则m的值是_______.
33.(2021·浙江·七年级期末)若是关于,的二元一次方程的一个解,则__________.
34.(2021·浙江·七年级期末)写出一个二元一次方程组是____________使它的解是.
35.(2021·浙江·七年级期末)已知二元一次方程组的解为,则_________.
36.(2021·浙江·杭州外国语学校七年级期末)若是的解,则满足的等量关系是__________.
37.(2021·浙江鄞州·七年级期末)将方程4x+3y=6变形成用y的代数式表示x,则x=________.
38.(2021·浙江柯桥·七年级期末)已知,则________.
39.(2021·浙江·七年级期末)如果实数m,n满足方程组,那么=______.
40.(2021·浙江·七年级期末)把方程(1﹣y)﹣x=0写成用含有x的式子表示y的形式,得y=____.
41.(2021·浙江越城·七年级期末)若方程组 的解是 ,则方程组 的解为__________________
42.(2021·浙江·七年级期末)已知关于x,y的二元一次方程组 的解互为相反数,则k的值是_________.
43.(2021·浙江·七年级期末)我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为__________尺,竿子长为__________尺.
44.(2021·浙江杭州·七年级期末)若关于x,y的二元一次方程组的解是正整数,则整数_______.
45.(2021·浙江·七年级期末)若方程组与方程组的解相同,则的值为______.
46.(2021·浙江·七年级期末)甲、乙两人练习跑步,如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙,若设甲的速度为x米/秒,乙的速度为y米/秒,可列方程组_____.
47.(2021·浙江·七年级期末)小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是__分钟.
48.(2021·浙江·杭州外国语学校七年级期末)有一片开心农场,蔬菜每天都在匀速生长,如果每天有20名游客摘菜,6天就能摘完;如果每天有17名游客摘菜,9天就能摘完(规定每名游客每天摘菜量相同),那么每天有14名游客摘菜,___天就能摘完.
49.(2021·浙江慈溪·七年级期末)学校设置了有关艺术类的甲、乙、丙三个拓展性课程项目,规定甲、乙两项不能兼报,学生选报后作了统计,发现报甲项目的人数与报乙项目的人数之和为报丙项目人数的;同时兼报甲、丙两项目的人数占报甲项目的人数的,同时兼报乙、丙两项目的人数占报乙项目的人数的;兼报甲、丙两项目的人数与兼报乙、丙两项目的人数之和是报丙项目人数的,则报甲、乙两个项目的人数之比为______.
50.(2021·浙江温岭·七年级期末)一个水池有,两个水口,其中为进水口,水口可进水也可出水(水口进出水速度相同).已知单独打开进水口,需要小时将水池由空池注满.若将,两个水口同时打开进水,小时将水池由空池注满;若将水口打开进水,同时水口打开出水,小时将水池由空池注满,则______.
51.(2021·浙江·七年级期末)对于实数x,y定义新运算其中a,b,c为常数,若,且有一个非零常数d,使得对于任意的x,恒有,则d的值是____.
三、解答题
52.(2021·浙江·杭州外国语学校七年级期末)解方程(组)
(1)
(2)
53.(2021·浙江柯桥·七年级期末)关于,的二元一次方程组与的解相同,求、的值.
54.(2021·浙江·七年级期末)解下列方程组:
(1)
(2)
55.(2021·浙江柯桥·七年级期末)解方程(组):
(1)
(2)
56.(2021·浙江·七年级期末)已知关于x、y的方程组 的解为 ,求m、n的值.
57.(2021·浙江·七年级期末)解方程组
(1)
(2)
58.(2021·浙江·七年级期末)解下列二元一次方程组:
(1)
(2)
59.(2021·浙江·七年级期末)解方程组:
(1)
(2)
60.(2021·浙江·七年级期末)(1)解方程组: (2)解方程组:
61.(2021·浙江·七年级期末)已知关于x,y的方程组
(1)请直接写出方程x+2y-6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
62.(2021·浙江·杭州外国语学校七年级期末)某中学为了表彰在书法比赛中成绩突出的学生,购买了钢笔30支,毛笔45支,共用了1755元,其中每支毛笔比钢笔贵4元.
(1)求钢笔和毛笔的单价各为多少元?
(2)①学校仍需要购买上面的两种笔共105支(每种笔的单价不变).陈老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领2447元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.
②陈老师突然想起,所做的预算中还包括校长让他买的一支签字笔.如果签字笔的单价为小于10元的整数,请通过计算,直接写出签字笔的单价可能为 元.
63.(2021·浙江·七年级期末)亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
64.(2021·浙江·七年级期末)某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
65.(2021·浙江·七年级期末)海南五月瓜果飘香,某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
66.(2021·浙江·七年级期末)某景点的门票价格如下表:
购票人数(人) 1~50 51~99 100以上(含100)
门票单价(元) 48 45 42
(1)某校七年级1、2两个班共有102 人去游览该景点,其中1班人数少于50人,2班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付4737 元,两个班各有多少名学生?
(2)该校八、九年级自愿报名浏览该景点,其中八年级的报名人数不超过50人,九年级的报名人数超过50人,但不超过80人.若两个年级分别购票,总计支付门票费4914元;若合在一起作为一个团体购票,总计支付门票费4452元,问八年级、九年级各报名多少人?
67.(2021·浙江·七年级期末)目前,新型冠状病毒在我国虽可控可防,但不可松懈.天府新区某校欲购置规格分别为300ml和500ml的甲、乙两种免洗手消毒液共300瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶.
(1)如果购买这两种消毒液共5550元,求甲、乙两种消毒液各购买多少瓶?
(2)在(1)的条件下,若该校在校师生共1320人,平均每人每天都需使用10ml的免洗手消毒液,则这批消毒液可使用多少天?
68.(2021·浙江温州·七年级期末)七年(1)(2)两班各40人参加垃圾分类知识竞赛,规则如图.比赛中,所有同学均按要求一对一连线,无多连、少连.
(1)分数5,10,15,20中,每人得分不可能是________分.
(2)七年(1)班有4人全错,其余成员中,满分人数是未满分人数的2倍;七年(2)班所有人都得分,最低分人数的2倍与其他未满分人数之和等于满分人数.
①问(1)班有多少人得满分?
②若(1)班除0分外,最低得分人数与其他未满分人数相等,问哪个班的总分高?
69.(2021·浙江·七年级期末)某大型超市投入15000元资金购进、两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价 成本价(元/箱) 销售价(元/箱)
A品牌 20 32
B品牌 35 50
(1)该大型超市购进、品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
70.(2021·浙江·七年级期末)为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户.若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.
(1)求医用口罩和洗手液的单价;
(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N95口罩.若需购买医用口罩,N95口罩共1200个,其中N95口罩不超过200个,钱恰好全部用完,则有几种购买方案,请列方程计算.
试卷第1页,共3页
参考答案:
1.A
【分析】
把代入方程,即可求解.
【详解】
∵是关于的二元一次方程的一组解,
∴,
∴a=-5,
故选:A
【点睛】
本题主要考查二元一次方程的解,掌握方程的解的定义,是解题的关键.
2.B
【分析】
二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
【详解】
解:A、是二元二次方程,故此选项不符合;
B、是二元一次方程,故此选项符合;
C、是分式方程,故此选项不符合;
D、是二元二次方程,故此选项不符合;
故选B.
【点睛】
此题主要考查了二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
3.B
【分析】
将代入方程3x y=5得出关于a的方程,解之可得.
【详解】
将代入方程3x y=5,得:3a+2a=5,
解得:a=1,
故选B.
【点睛】
此题考查二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
4.B
【分析】
将各项中x与y的值代入方程检验即可.
【详解】
解:A、把代入方程得:左边=2-5=-3,右边=6,左边≠右边,不符合题意;
B、把代入方程得:左边=8-2=6,右边=6,左边=右边,符合题意;
C、把代入方程得:左边=4-4=0,右边=6,左边≠右边,不符合题意;
D、把代入方程得:左边=4-3=1,右边=6,左边≠右边,不符合题意;
故选:B.
【点睛】
此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
5.B
【分析】
根据二元一次方程的定义求解可得答案.
【详解】
解:(1),是二元一次方程;
(2),是二元一次方程;
(3),是一元二次方程;
(4),是一元一次方程;
故选:B.
【点睛】
本题考查了二元一次方程的定义,二元一次方程的定义是含有两个未知数且未知数的次数都为1.
6.B
【分析】
根据二元一次方程2x-y=1的解有无数个,所以此题应该用排除法确定答案,分别代入方程组,使方程左右相等的解才是方程组的解.
【详解】
解:A、把x=0,y=10.5代入方程,左边=-10.5≠1=右边,所以不符合题意;
B、把x=4,y=7代入方程,左边=1=右边,所以符合题意;
C、把x=1,y=11代入方程,左边=-9≠1=右边,所以不符合题意;
D、把x=15,y=11代入方程,左边=19≠1=右边,所以不符合题意.
故选:B.
【点睛】
本题考查了二元一次方程的解,要求理解什么是二元一次方程的解,并会把x,y的值代入原方程进行验证.
7.D
【分析】
根据已知将代入二元一次方程组得到m,n的值,即可求得m-n的值.
【详解】
∵是二元一次方程组
∴
∴m=1,n=-3
m-n=4
故选:D
【点睛】
本题考查了二元一次方程组解的定义,已知二元一次方程组的解,可求得方程组中的参数.
8.A
【分析】
把①变形,用y表示出x的值,再代入②得到关于y的方程,令y的系数等于0即可求出ab的值.
【详解】
,
由①得,x=-1-ay,
代入②得,b(-1-ay)-2y+a=0,
即(-ab-2)y=b-a,
因为此方程组没有实数根,所以b-a ≠0且-ab-2=0
解得ab=-2.
故选A.
【点睛】
考查的是解二元一次方程组,解答此类问题时要熟知解二元一次方程组的代入消元法和加减消元法.
9.A
【分析】
将x=1代入方程x+y=3求得y的值,将x、y的值代入x+py=0,可得关于p的方程,可求得p.
【详解】
解:根据题意,将x=1代入x+y=3,可得y=2,
将x=1,y=2代入x+py=0,得:1+2p=0,
解得:p=-,
故选:A.
【点睛】
本题主要考查二元一次方程组的解的概念,根据方程组的解会准确将方程的解代入是前提,严格遵循解方程的基本步骤求得方程的解是关键.
10.C
【详解】
①解方程组,
由②可知,代入①中,可得,
故方程组的解为,
∵,
∴,,
∴不是方程组的解,①错误.
②时,,,,互为相反数,②正确;
③时,,,满足,③正确;
④当时,,得,综合,在时,且.
∴,
∴,④正确.
故选.
点睛:本题考查了二元一次方程组的解,解一元一次不等式组.关键是根据条件,求出x、y的表达式及x、y的取值范围.
11.A
【分析】
根据方程的解的定义,将方程2x-y=14中x,y用k替换得到k的一元一次方程,进行求解.
【详解】
将代入二元一次方程2x-y=14,得
7k=14,
解得k=2.
故选A.
【点睛】
考查了二元一次方程的解的定义,只需把方程的解代入,进一步解一元一次方程即可.
12.C
【详解】
由题意得:x=y,
∴4x+3x=14,
∴x=2,y=2,
把它代入方程kx+(k-1)y=6得2k+2(k-1)=6,
解得k=2.
故选C.
13.D
【分析】
根据各选项分别计算,即可解答.
【详解】
方程组利用加减消元法变形即可.
解:A、①×2﹣②可以消元x,不符合题意;
B、②×(﹣3)﹣①可以消元y,不符合题意;
C、①×(﹣2)+②可以消元x,不符合题意;
D、①﹣②×3无法消元,符合题意.
故选:D.
【点睛】
本题考查了加减消元法解二元一次方程组,只有当两个二元一次方程未知数的系数相同或相反时才可以用加减法消元,系数相同相减消元,系数相反相加消元.
14.D
【详解】
本题考查了加减法解二元一次方程组
用加减法解二元一次方程组时,必须使同一未知数的系数相等或者互为相反数.如果系数相等,那么相减消元;如果系数互为相反数,那么相加消元.
A、,可消去x,故不合题意;
B、,可消去y,故不合题意;
C、,可消去x,故不合题意;
D、,得,不能消去y,符合题意.
故选D.
15.B
【分析】
将代入方程组,然后利用加减消元法解方程组,从而求解.
【详解】
解:∵是关于x,y的二元一次方程组的解
∴,解得:
∴a+b=-1
故选:B.
【点睛】
本题考查解二元一次方程组,掌握加减消元法解方程组的步骤和计算法则,正确计算是解题关键.
16.C
【分析】
将代入二元一次方程组中解出x和y的值,再计算x+2y的算术平方根即可.
【详解】
解:将代入二元一次方程中,
得到:,解这个关于x和y的二元一次方程组,
两式相加,解得,将回代方程中,解得,
∴,
∴x+2y的算术平方根为,
故选:C.
【点睛】
本题考查了二元一次方程组的解法,算术平方根的概念等,熟练掌握二元一次方程组的解法是解决本题的关键.
17.D
【分析】
采用加减消元法解方程组即可.
【详解】
①-②得:
∴
将代入①得:
∴
∴方程组的解为
故选D.
【点睛】
本题考查解二元一次方程组,熟练掌握消元法是解题的关键.
18.A
【分析】
①把a看做已知数表示出方程组的解,把a=0代入求出x与y的值,代入方程检验即可;②令x=y求出a的值,即可作出判断;③把x与y代入3x-y中计算得到结果,判断即可;④令2x=3y求出a的值,判断即可.
【详解】
解:,
①+②得:3x=3a-6,
解得:x=a-2,
把x=a-2代入①得:y=3a+3,
当a=0时,x=-2,y=3,
把x=-2,y=3代入x+y=1得:左边=-2+3=1,右边=1,是方程的解;
当x=y时,a-2=3a+3,即a=;
3x-y=3a-6-3a-3=-9,无论a为什么实数,3x-y的值始终不变,为-9;
令2x=3y,即2a-4=9a+9,即a=,存在,
则正确的结论是①②③,
故选A.
【点睛】
此题考查了二元一次方程组的解,二元一次方程的解,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.
19.A
【分析】
设索长为x尺,竿子长为y尺,根据“索比竿子长一托,折回索子却量竿,却比竿子短一托”,即可得出关于x、y的二元一次方程组.
【详解】
设索长为x尺,竿子长为y尺,
根据题意得:.
故选A.
【点睛】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
20.A
【分析】
根据“一根绳子去量一根木条,绳子剩余4.5尺”可知:绳子=木条+4.5,再根据“将绳子对折再量木条,木条剩余1尺”可知:绳子=木条-1,据此列出方程组即可.
【详解】
解:设木条长x尺,绳子长y尺,
那么可列方程组为:,
故选:A.
【点睛】
本题考查二元一次方程组的实际应用,解题的关键是明确题意,找出等量关系,列出相应的二元一次方程组.
21.D
【分析】
设马每匹x两,牛每头y两,根据“马四匹、牛六头,共价四十八两与马三匹、牛五头,共价三十八两列方程组即可.
【详解】
设马每匹x两,牛每头y两,由题意得
.
故选D.
【点睛】
本题考查了二元一次方程组的应用,仔细审题,找出题目的已知量和未知量,设两个未知数,并找出两个能代表题目数量关系的等量关系,然后列出方程组求解即可.
22.A
【分析】
设小长方形的长为xcm,小长方形的宽为ycm,根据图示,找出等量关系,列方程组求解.
【详解】
解:设小长方形的长为xcm,小长方形的宽为ycm,
由题意得,,
解得:,
小长方形的面积为:40×10=400(cm2).
故选A.
【点睛】
本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
23.B
【分析】
由用于生产笔管和笔套的短竹的数量结合生产的笔管总数=笔套的总数,即可得出关于x,y的二元一次方程组,此题得解.
【详解】
解:依题意,得:.
故选:B.
【点睛】
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
24.A
【分析】
分别设做了竖式无盖纸盒x个,横式无盖纸盒y个,列二元一次方程组,把两个方程的两边分别相加得,易知的值一定是5的倍数,本题即解答.
【详解】
解:设做成竖式无盖纸盒x个,横式无盖纸盒y个,根据题意列方程组得:
,
则两式相加得
,
∵x、y 都是正整数
∴一定是5的倍数;
∵200、201、202、203四个数中,只有200是5的倍数,
∴的值可能是200.
故选A.
【点睛】
本题主要考查二元一次方程组的实际应用;巧妙处理所列方程组,使两方程相加得出,是解答本题的关键.
25.B
【分析】
设铅笔单价为x元,橡皮的单价为y元,日记本的单价为z元,由题意:买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,列出方程组,求出x+y+z=6,即可求解.
【详解】
解:设铅笔单价为x元,橡皮的单价为y元,日记本的单价为z元,
由题意得:,
由①×2-②得:x+y+z=6,
∴10x+10y+10z=10×6=60,
即购买10支铅笔、10块橡皮与10本日记本共需60元,
故选:B.
【点睛】
本题考查了三元一次方程组的应用以及“整体思想”等知识;熟练掌握“整体思想”,找出等量关系列出方程组是解题的关键.
26.C
【分析】
先解出x、y的值,代入③,转化为关于k的方程来解.
【详解】
解:由题意可得,
①×3+②得11x-22=0,
解得x=2,
代入①得y=-1,
将x=2,y=-1代入③得,
-1-2k+9=0,
解得k=4.
故选:C.
【点睛】
本题实质是解三元一次方程组,先用了加减消元法求得x,y后,再求得k的值.
27.1346
【分析】
先化简绝对值,再根据方程取非负整数解即可.
【详解】
解:∵,
∴,
∵a,b,c为3个自然数,
要想取最大值,a应该取最小值0,
代入得,,
当b=1时,c最大,最大值为673,
,
故答案为:1346.
【点睛】
本题考查了绝对值化简和不定方程求非负整数解,解题关键是根据题意化简绝对值并确定a、b、c的最值.
28.8
【分析】
根据二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程可得|m|-2=1,2m-n=1,解出m、n的值可得答案.
【详解】
解:由题意,知|m|-2=1,2m-n=1且m+3≠0.
解得m=3,n=5.
所以m+n=3+5=8.
故答案是:8.
【点睛】
主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.
29. -2, -1
【分析】
先根据互为相反数的和等于0列式,再根据非负数的性质列出二元一次方程组,最后解二元一次方程组求出、的值.
【详解】
与互为相反数,
,
,
② ①得,,
解得,
把代入①得,,
解得.
故答案为;.
【点睛】
本题考查了绝对值非负数,算术平方根非负数的性质,以及二元一次方程组的解法,根据几个非负数的和等于0,则每一个算术都等于0列式是解题的关键.
30.2或4
【分析】
根据二元一次方程的定义,可得x和y的指数分别都为1,列关于m、n的方程,然后求解即可.
【详解】
根据二元一次方程的定义:
解得:m=3,,
∴m+n=3+1=4或m+n=3-1=2;
故答案为:2或4.
【点睛】
本题考查二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程.
31.-1
【分析】
将x与y的值代入方程即可求出a的值.
【详解】
解:将x=3,y=1代入x+ay=2得:3+a=2,
解得:a=-1.
故答案为:-1.
【点睛】
此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
32.5
【分析】
直接将解代入方程即可求出m.
【详解】
把代入得, , .
【点睛】
本题考查方程的解的概念,给出方程的解,只需将解代入方程计算即可.
33.3
【分析】
根据二元一次方程的解定义,将x和y的值代入求解即可.
【详解】
由题意,将代入二元一次方程得:
解得
故答案为:3.
【点睛】
本题考查了二元一次方程的解定义,掌握解的定义是解题关键.
34.
【分析】
由1与-2列出两个算式,即可确定出所求方程组.
【详解】
解:根据题意得:,
故答案为:.
【点睛】
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
35.
【分析】
将代入计算即可.
【详解】
解:将代入,得
,
解得:,
∴,
故答案为:.
【点睛】
本题考查了二元一次方程组的解,将原方程的解代入原方程是解决本题的关键.
36.
【分析】
直接把代入方程组,然后消去c,即可得到答案.
【详解】
解:把代入方程组,得
,
由①×2:,③
由②+③:,
∴;
故答案为:.
【点睛】
本题考查了加减消元法解二元一次方程组,以及方程组的解,解题的关键是掌握加减消元法进行解题.
37.
【详解】
解:
4x=6-3y
x=
故答案为:.
38.4
【分析】
利用非负数的性质列出关于x与y的方程组,求出方程组的解得到x与y的值,即可求出所求式子的值.
【详解】
解:∵,
∴,
解得:,
∴4,
故答案为:4.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
39.1
【分析】
方程组中的两个方程相减可得,然后整体代入所求式子计算即可.
【详解】
解:对方程组,①-②,得,
所以.
故答案为:﹣1.
【点睛】
本题考查了二元一次方程组的解法和代数式求值,灵活应用整体的思想是解题的关键.
40.1﹣3x
【分析】
方程两边同乘以3后,再根据等式的性质进行变形即可求解.
【详解】
(1﹣y)﹣x=0,
1﹣y﹣3x=0,
即y=1﹣3x.
故答案为:1﹣3x.
【点睛】
本题考查了解二元一次方程,能正确根据等式的性质进行变形是解题的关键.
41.x=5.3,y=0.3
【分析】
通过观察两个方程组之间的关系,可得到,即可求解.
【详解】
方程组 的解是 ,
中,,
解得,
方程组的解为,
故答案为:x=5.3,y=0.3.
【点睛】
本题考查二元一次方程组的解,要比较两个方程组的结构相似处,得出是解题的关键.
42.-1
【详解】
∵关于x,y的二元一次方程组 的解互为相反数,
∴x=-y③,
把③代入②得:-y+2y=-1,
解得y=-1,所以x=1,
把x=1,y=-1代入①得2-3=k,
即k=-1.
故答案为-1
43. 20 15
【分析】
设索长为尺,竿子长为尺.根据题目中的等量关系列方程组求解即可.
【详解】
解:设索长为尺,竿子长为尺.根据题意得:
解得:
故答案为20,15.
【点评】
考查二元一次方程组的应用,解题的关键是找到题目中的等量关系.
44.0,3,4,5
【分析】
先解方程组,用m表示出方程组的解,根据方程组有正整数解得出m的值.
【详解】
解:
由②得:x=3y ③,
把③代入①得:6y my=6,
∴y=,
∴x=,
∵方程组的解是正整数,
∴6 m>0,
∴m<6,并且和是正整数,m是整数,
∴m的值为:0,3,4,5.
故答案是:0,3,4,5.
【点睛】
本题考查了二元一次方程组的解,一般情况下二元一次方程组的解是唯一的.数学概念是数学的基础与出发点,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.
45.2
【分析】
把代入方程组,得到一个关于a,b的方程组,将方程组的两个方程左右两边分别相加,整理即可得出a+b的值.
【详解】
解:把代入方程组,
得:,
①+②,得:7(a+b)=14,
则a+b=2.
故选:2.
【点睛】
此题主要考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.理解定义是关键.
46.
【分析】
根据题意,得出等量关系:①乙先跑10米,则甲跑5秒就可以追上乙;②乙先跑2秒,则甲跑4秒就可追上乙,得出方程组即可.
【详解】
解:根据乙先跑10米,则甲跑5秒就可以追上乙,得方程5x=5y+10;
根据乙先跑2秒,则甲跑4秒就可追上乙,得方程4x=4y+2y.
可得方程组.
故答案为:.
【点睛】
本题考查了二元一次方程组的应用,弄清题意,找准等量关系列出相应方程是解题的关键.
47.4
【分析】
设同向行驶的相邻两车的距离及车、小王的速度为未知数,等量关系为:6×车速-6×小王的速度=同向行驶的相邻两车的距离;3×车速+3×小王的速度=同向行驶的相邻两车的距离;把相关数值代入可得同向行驶的相邻两车的距离及车的速度关系式,相除可得所求时间.
【详解】
解:设18路公交车的速度是x米/分,小王行走的速度是y米/分,同向行驶的相邻两车的间距为s米.
每隔6分钟从背后开过一辆18路公交车,则6x-6y=s.①
每隔3分钟从迎面驶来一辆18路公交车,则3x+3y=s.②
由①,②可得s=4x,
∴.
故答案为:4.
即18路公交车总站发车间隔的时间是4分钟.
【点睛】
本题考查二元一次方程组的应用;根据追及问题和相遇问题得到两个等量关系是解决本题的关键;设出所需的多个未知数是解决本题的突破点.
48.18
【分析】
首先设原有蔬菜量为a,每天生长的蔬菜量为b,每名游客每天摘菜量为c,有14名游客摘菜x天就能摘完.根据“原蔬菜量+每天生长的蔬菜量×采摘天数=每名游客每天摘菜量×人数×天数”列出方程组,可解得x的值即为所求.
【详解】
解:首先设原有蔬菜量为a,每天生长的蔬菜量为b,每名游客每天摘菜量为c,有14名游客摘菜x天就能摘完,
依题意得 ,
由②﹣①得:
由③﹣②得:
将④代入⑤得:,
解得:
故答案是:18.
【点睛】
本题考查方程组的应用,有些应用题,它所涉及到的量比较多,量与量之间的关系也不明显,需增设一些表知数辅助建立方程,辅助表知数的引入,在已知条件与所求结论之间架起了一座“桥梁”,对这种辅助未知量,并不能或不需求出,可以在解题中相消或相约,这就是我们常说的“设而不求.”
49..
【分析】
设报甲项目的有x人,报乙项目的有y人,报丙项目的有z人,根据题意即可得出关于x,y,z的三元一次方程组,然后进一步化简即可得出答案;
【详解】
解:设报甲项目的有x人,报乙项目的有y人,报丙项目的有z人,
依题意得:
由①得:
将③代入②得:
化简得:
∴x:y=1:2.
故答案为:1:2.
【点睛】
本题考查了三元一次方程组的应用,找准等量关系,正确列出三元一次方程组是解题的关键.
50.
【分析】
设进水口速度为,进水口、出水口速度为,水池容量为,由题意,列出方程组求解即可.
【详解】
解:设进水口速度为,进水口、出水口速度为,水池容量为,
由题意得:,
由②③得:
,
解得:,
将代入①得:
,
解得:,
故答案为:.
【点睛】
本题考查了列方程组及求解,解题的关键是找准题中等量关系列出方程组即可.
51.4
【分析】
由新定义的运算,及,,构造方程组,不难得到参数,,之间的关系.又由有一个非零实数,使得对于任意实数,都有,可以得到一个关于的方程,解方程即可求出满足条件的的值.
【详解】
解:,
由,,即,
,.
又由对于任意实数恒成立,
,
为非零实数,
,
.
.
.
.
故答案为:4.
【点睛】
本题属于新定义的题目,根据新运算的定义,将已知中的数据代入进行运算是关键,同时考查了学生合情推理的能力,属于中档题.
52.(1);(2)
【分析】
(1)先利用分数的基本性质把方程化为:,再去分母,去括号,整理得:,从而可得答案;
(2)把视为整体未知数,先消去,求解 再求解 再求解即可得到答案.
【详解】
解:(1)
去分母得:
去括号得:
解得:
(2)
①×12得:,③
②+③得:
④
把代入②得:
⑤
④+⑤得:
把代入⑤得:
∴方程组的解为:
【点睛】
本题考查的是一元一次方程的解法,二元一次方程组的解法,根据方程的特点选择整体消元的解法是解题的关键.
53.,
【分析】
根据加减法,可得第二个方程组的解,根据方程组的解相同,可把第二个方程组的解代入第一个方程组,可得关于a、b的方程组,根据解方程组,可得答案.
【详解】
解:解得,
由的二元一次方程组与的解相同,得
,
①+②,得,
解得.
把代入①,得.解得.
【点睛】
本题考查了二元一次方程组的解,把方程组的解代入第一个方程组得出关于a、b的二元一次方程组是解题关键.
54.(1);(2)
【分析】
(1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【详解】
解:(1),
①+②得:6x=42,
解得:x=7,代入①中,
解得:y=9,
则方程组的解为;
(2)方程组化简为,
①+②得:3x=7,
解得:x=,代入①中,
解得:y=,
则方程组的解为.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
55.(1);(2)y=0
【分析】
(1)利用加减消元法求解可得.
(2)方程去分母,去括号,移项合并,把y系数化为1,即可求出解.
【详解】
解:(1),
①×3+②,得:5x=20,
解得:x=4,
将x=4代入①,得:4-y=2,
解得:y=2,
所以方程组的解为;
(2)去分母得:3y+6-4y+6=12,
移项合并得:-y=0,
解得:y=0.
【点睛】
此题考查了解一元一次方程,解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
56.m=1,n=1.
【详解】
试题分析:把x与y的值代入方程组得出关于的二元一次方程组,求得方程组的解即可.
试题解析:∵关于x、y的方程组 的解为
∴
解得:
即m=1,n=1.
57.(1);(2)
【分析】
(1)利用代入消元法求解即可;
(2)利用加减消元法求解即可;
【详解】
解:(1),
将②代入①中,得
3x-5(x+1)=3,
解得:x=-4,代入中②,
解得:y=-3,
∴原方程组的解为;
(2),
①×3+②×4得:
25x=50,解得:x=2,代入①中,
解得:y=1,
∴原方程组的解为.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
58.(1);(2)
【分析】
(1)令方程组的两个方程分别为①和②,将①代入②即可求得x的值,再将求得的x的值代入①可求得y的值;
(2)令方程组的两个方程分别为①和②,先化简②得到③,①×2得到④,④-③可求得y的值,将y值代入①,即可求得x的值;
【详解】
(1)
将①代入②,得7x=14
解得x=2
将x=2代入①,得y=8
∴方程组的解为:
故答案为:
(2)
由②,得③
①×2,得④
④-③,得13y=13
解得y=1
将y=1代入①,得2x=5
解得x=
故方程组的解为:
故答案为:
【点睛】
本题考查了二元一次方程组的解法,分别用到了代入消元法和加减消元法,代入消元法是将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入另一个方程中,消去一个未知数,得到一个一元一次方程,最后求得方程组的解;当方程中两个方程的某一未知数的系数相等或互为相反数时,把这两个方程的两边相加或相减来消去这个未知数,从而将二元一次方程化为一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法.
59.(1);(2).
【分析】
(1)利用代入消元法解二元一次方程组即可得;
(2)先通过去分母将方程组进行简单变形,再利用加减消元法解二元一次方程组即可得.
【详解】
(1),
将①代入②得:,
解得,
将代入②得:,
解得,
则方程组的解为;
(2)可变形为,
由①②得:,
解得,
将代入①得:,
解得,
则原方程组的解为.
【点睛】
本题考查了利用消元法解二元一次方程组,熟练掌握方程组的解法是解题关键.
60.(1);(2)
【分析】
(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【详解】
解:(1)把(1)代入(2)得:3(y+1)+y=7,
解得:y=1,
把y=1代入(1)得:x=1+1=2,
则方程组的解为;
(2)(2)×5-(1)×2得:21y=20,
解得:y=代入(2)得:2x+5×=8,
解得:x=,
则方程组的解为.
【点睛】
此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.
61.(1), (2)m=(3)(4)
【分析】
(1)先对方程变形为x=6-2y,然后可带入数值求解;
(2)把已知的x+y=0和方程x+2y-6=0组合成方程组,求解方程组的解,然后代入方程x-2y+mx+5=0即可求m的值;
(3)方程整理后,根据无论m如何变化,二元一次方程组总有一个固定的解,列出方程组,解方程组即可;
(4)先把m当做已知求出x、y的值,然后再根据整数解进行判断即可.
【详解】
(1)
(2) 解得
把代入,解得m=
(3)
(4)
①+②得:
解得,
∵x恰为整数,m也为整数,
∴2+m=1或2+m=-1,
解得
62.(1) 钢笔的单价为21元,毛笔的单价为25元;(2)①见解析;②签字笔的单价可能为2元或6元.
【分析】
(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元.根据买钢笔30支,毛笔45支,共用了1755元建立方程,求出其解即可;
(2)①根据第一问的结论设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105 y)支,求出方程的解不是整数则说明算错了;
②设单价为21元的钢笔为z支,单价为25元的毛笔则为(105 y)支,签字笔的单价为a元,根据条件建立方程求出其解就可以得出结论.
【详解】
解:(1)设钢笔的单价为x元,则毛笔的单价为(x+4)元.由题意得:
30x+45(x+4)=1755,
解得:x=21,
∴毛笔的单价为:x+4=25.
答:钢笔的单价为21元,毛笔的单价为25元.
(2)①设单价为21元的钢笔为y支,所以单价为25元的毛笔则为(105﹣y)支.根据题意,得
21y+25(105﹣y)=2447.
解之得:y=44.5 (不符合题意).
∴陈老师肯定搞错了.
②设单价为21元的钢笔为z支,签字笔的单价为a元,则根据题意,得
21z+25(105﹣z)=2447﹣a.
∴4z=178+a,
∵a、z都是整数,
∴178+a应被4整除,
∴a为偶数,又因为a为小于10元的整数,
∴a可能为2、4、6、8.
当a=2时,4z=180,z=45,符合题意;
当a=4时,4z=182,z=45.5,不符合题意;
当a=6时,4z=184,z=46,符合题意;
当a=8时,4z=186,z=46.5,不符合题意.
所以签字笔的单价可能2元或6元.
故答案为2元或6元.
【点睛】
本题考查了列二元一次方程组解实际问题的运用,列一元一次方程解实际问题的运用及二元一次不定方程的运用,在解答时根据题意等量关系建立方程是关键.
63.(1)计划36座的新能源客车6辆,共有218名志愿者;(2)调配36座新能源客车3辆,22座新能源客车5辆.
【分析】
(1)设计划调配36座新能源客车辆,该大学共有名志愿者.列方程组,得解方程组可得;(2)设调配36座新能源客车辆,22座新能源客车辆,根据题意,得,求正整数解;
【详解】
解:(1)设计划调配36座新能源客车辆,该大学共有名志愿者.
列方程组,得
解得
∴计划36座的新能源客车6辆,共有218名志愿者.
(2)设调配36座新能源客车辆,22座新能源客车辆,
根据题意,得,正整数解为
∴调配36座新能源客车3辆,22座新能源客车5辆.
【点睛】
考核知识点:二元一次方程组的运用.理解题意是关键.
64.(1)1辆小客车和1辆大客车都坐满后一次可送65名学生(2)租车方案有3种,①小客车20辆,大客车0辆;②小客车11辆,大客车4辆;③小客车2辆,大客车8辆(3)租小客车2辆,大客车8辆最省钱
【分析】
(1)设1辆小客车一次可送学生x人,1辆大客车都坐满后一次可送y名学生,根据题意可得等量关系:①用3辆小客车拉的人数+1辆大客车拉的人数=运送学生105人;②用1辆小客车拉的人数+2辆大客车拉的人数=运送学生110人,根据等量关系列出方程组,再解即可;
(2)设租小客车a辆,大客车b辆,由题意得:20×小客车的数量+45×大客车的数量=400人,根据等量关系列出方程,求出非负整数解即可;
(3)分别计算出每种租车方案的钱数,进行比较即可.
【详解】
(1)设1辆小客车一次可送学生x人,1辆大客车都坐满后一次可送y名学生,
由题意得:,
解得:,
所以x+y=65,
答:1辆小客车和1辆大客车都坐满后一次可送65名学生;
(2)设租小客车a辆,大客车b辆,由题意得:
20a+45b=400,可变形为,
∵每辆汽车恰好都坐满,
∴a、b的值均为非负整数,
∴a、b可取,,,
∴租车方案有3种,①小客车20辆,大客车0辆;②小客车11辆,大客车4辆;③小客车2辆,大客车8辆;
(3)各种租车费用:①20×200=4000(元);②11×200+4×380=3720(元);③2×200+8×380=3440(元);
∵3440<3720<4000,
∴租小客车2辆,大客车8辆最省钱
65.李叔叔购买“无核荔枝”12千克,购买“鸡蛋芒果”18千克..
【分析】
设李叔叔购买“无核荔枝”x千克,购买“鸡蛋芒果”y千克,根据总质量为30千克,总花费为708元,可得出方程组,解出即可.
【详解】
解:设李叔叔购买“无核荔枝” x千克,购买“鸡蛋芒果” y千克,
由题意,得:,解得:.
答:李叔叔购买“无核荔枝”12千克,购买“鸡蛋芒果”18千克.
66.(1)1班有49名学生,2班有53名学生;(2)八年级报名48人,九年级报名58人
【分析】
(1)设七年级1班有名学生,2班有名学生,由题意列出二元一次方程组,解方程组即可;
(2)设八年级报名人,九年级报名人,分两种情况:①若,②若,由题意分别列出方程组,解方程组即可.
【详解】
解:(1)设七年级1班有x名学生,2班有y名学生,
由题意得:,
解得:,
答:七年级1班有49名学生,2班有53名学生;
(2)设八年级报名x人,九年级报名y人,
分两种情况:
①若,
由题意得:,
解得:,(不合题意舍去);
②若,
由题意得:,
解得:,符合题意;
答:八年级报名48人,九年级报名58人.
【点睛】
本题主要考查了二元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.注意(2)要分两种情况作答.
67.(1)甲种消毒液购买90瓶,乙种消毒液购买210瓶;(2)这批消毒液可使用10天
【分析】
(1)设甲种消毒液购买x瓶,乙种消毒液购买y瓶,由甲、乙两种免洗手消毒液共300瓶,其中甲消毒液15元/瓶,乙消毒液20元/瓶,列出方程组,即可求解;
(2)设这批消毒液可使用a天,由该校在校师生共1320人,平均每人每天都需使用10ml的免洗手消毒液,列出方程可求解.
【详解】
解:(1)设甲种消毒液购买x瓶,乙种消毒液购买y瓶,
由题意可得:,
解得:,
答:甲种消毒液购买90瓶,乙种消毒液购买210瓶;
(2)设这批消毒液可使用a天,
由题意可得:1320×10×a=90×300+500×210,
解得:a=10,
答:这批消毒液可使用10天.
【点睛】
本题考查了二元一次方程组的应用,一元一次方程的应用,根据题意列出方程和方程组是解答本题的关键.
68.(1)15;(2)①七年级(1)班有24人得满分;②七年级(2)班的总分高.
【分析】
(1)分别对连正确的数量进行分析,即可得到答案;
(2)①设七年(1)班满分人数有x人,则未满分的有人,然后列出方程,解方程即可得到答案;
②根据题意,先求出两个班各分数段的人数,然后求出各班的总分,即可进行比较.
【详解】
解:(1)根据题意,
连对0个得分为0分;
连对一个得分为5分;
连对两个得分为10分;
连对四个得分为20分;
不存在连对三个的情况,则得15分是不可能的;
故答案为:15.
(2)①根据题意,
设七年(1)班满分人数有x人,则未满分的有人,则
,
解得:,
∴(1)班有24人得满分;
②根据题意,(1)班中除0分外,最低得分人数与其他未满分人数相等,
∴(1)班得5分和10分的人数相等,
人数为:(人);
∴(1)班得总分为:(分);
由题意,(2)班存在得5分、得10分、得20分,三种情况,
设得5分的有y人,得10分的有z人,满分20分的有人,
∴,
∴,
∴七(2)班得总分为:
(分);
∵,
∴七(2)班的总分高.
【点睛】
本题考查了二元一次方程的应用,一元一次方程的应用,解题的关键是熟练掌握题意,正确掌握题目的等量关系,列出方程进行解题.
69.(1)该超市进品牌矿泉水400箱,品牌矿泉水200箱;(2)该超市共获利润7800元.
【分析】
(1)设该超市进A品牌矿泉水x箱,B品牌矿泉水y箱,“购进、两种品牌的矿泉水共600箱”和“投入15000元资金”,可列二元一次方程组,求解即可;
(2)根据 “总利润=A品牌矿泉水每箱利润×数量+ B品牌矿泉水每箱利润×数量”,即可求出该超市销售完600箱矿泉水获得的利润.
【详解】
解:(1)设该超市进品牌矿泉水箱,品牌矿泉水箱,
依题意,得:,
解得:.
答:该超市进品牌矿泉水400箱,品牌矿泉水200箱.
(2)(元)
答:该超市共获利润7800元.
【点睛】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
70.(1)医用口罩的单价为2.5元/个,洗手液的单价为30元/瓶;(2)有3种购买方案,方程见解析
【分析】
(1)设医用口罩的单价为x元/个,洗手液的单价为y元/瓶,根据题意列出二元一次方程组,解方程组即可;
(2)设增加购买N95口罩a个,洗手液b瓶,则医用口罩(1200-a)个,根据题意列出方程,将b用a表示出来,根据a,b都为正整数,得出满足题意的a,b的值.
【详解】
(1)设医用口罩的单价为x元/个,洗手液的单价为y元/瓶,根据题意得
解得
∴医用口罩的单价为2.5元/个,洗手液的单价为30元/瓶.
故答案为:医用口罩的单价为2.5元/个,洗手液的单价为30元/瓶
(2)设增加购买N95口罩a个,洗手液b瓶,则医用口罩(1200-a)个,根据题意得
6a+2.5(1200-a)+30b=5400
化简,得7a+60b=4800
∴b=80-
∵a,b都为正整数
∴a为60的倍数,且a≤200
∴,,
∴有三种购买方案
故答案为:有3种购买方案,方程见解析
【点睛】
本题考查了二元一次方程组的应用,先找到题中未知量,根据题中的等量关系,列出方程,解方程,对方程的解进行检验,舍去不符合题意的解.
答案第1页,共2页
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
