3.1同底数幂的乘法(1) 课件(共22张PPT)
文档属性
| 名称 | 3.1同底数幂的乘法(1) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-07 11:18:35 | ||
图片预览







文档简介
(共22张PPT)
3.1同底数幂的乘法(1)
第1课时
浙教版 七年级下
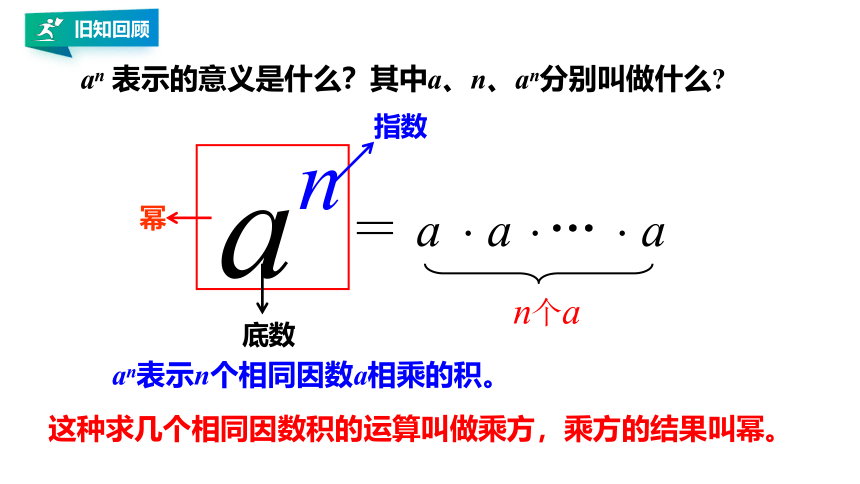
指数
底数
幂
an 表示的意义是什么?其中a、n、an分别叫做什么
an表示n个相同因数a相乘的积。
这种求几个相同因数积的运算叫做乘方,乘方的结果叫幂。
旧知回顾
(1)25 表示________________;
(2)10×10×10×10写成幂的形式____;
(3) a的底数是__,指数是__;
(4) (a+b)3 的底数是______,指数是_____;
(5) (-2)4 的底数是___,指数是__;
(6) -24 的底数是___,指数是__.
2×2×2×2×2(5个2相乘)
104
a
1
a+b
3
-2
4
2
4
幂的底数是分数、负数或者多项式时,底数应该添加括号。
-24表示24的相反数
填空:
同底数幂是指底数相同的幂
不是
旧知回顾
根据乘方的意义,以及有理数的乘法,请完成下列问题:
(1) 是多少个2相乘?
(2) ( ) ( )
=
(3) ( ) ( )
=
5
3
2
7
2
5
7
4
3
思考:通过对以上过程的观察,你能发现什么规律吗?
猜想:am · an = (m、n都是正整数)
能用一个式子来表达这个规律吗?
用字母来表示一般规律
新知导入
猜想: am · an= (m、n都是正整数)
am · an =
m个a
n个a
= a·a·····a
=am+n
(m+n)个a
即:
am · an = am+n (m、n都是正整数)
(a·a·····a)
am+n
(乘法结合律)
(乘方的意义)
(乘方的意义)
(a·a·····a)
你能解释猜想am · an=am+n正确吗?
回顾探究的过程,我们经历了怎样的过程?
经历“观察-猜想-验证-概括”的过程
利用乘方的意义推理说明
新知导入
am · an = am+n (m、n都是正整数)
同底数幂相乘,
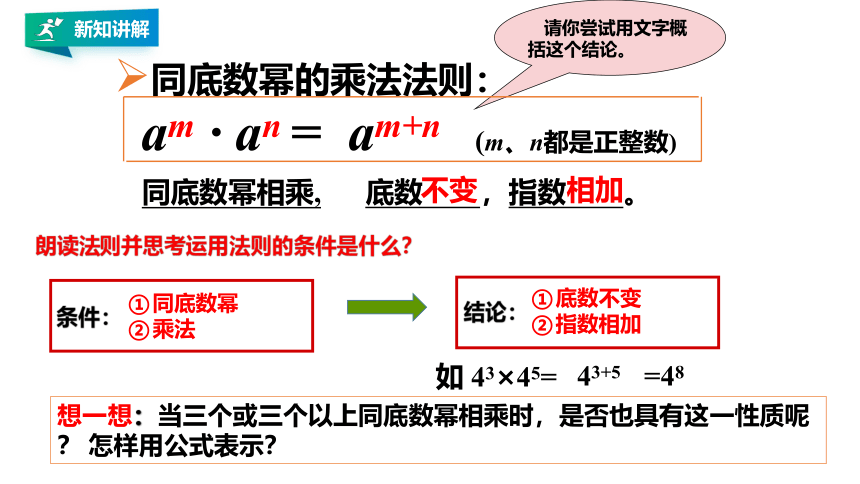
想一想:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法法则:
请你尝试用文字概括这个结论。
如 43×45=
43+5
=48
朗读法则并思考运用法则的条件是什么?
同底数幂
乘法
条件:
底数不变
指数相加
结论:
新知讲解
am · an · ap 等于什么?
猜想:
am· an· ap = am+n+p (m、n、p都是正整数)
方法2
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
方法1
am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
当三个或三个以上同底数幂相乘时,同底数幂乘法法则同样适用
新知讲解
下列各式哪些是同底数幂的乘法
法则运用的条件:①同底数幂 ②乘法
课堂练习
例1 计算下列各式,结果用幂的形式表示.
(1)
(2)
(3)
(4)
问题:这些式子是否能直接利用法则计算?
满足“底数相同,乘法运算”可以直接用法则。运算后结果:底数不变,指数相加。
运算结果的底数一般应化为正数,负数的奇数次幂为负。负数的偶数次幂为正。
指数为1时可省略不写,在运算时不能丢。
底数a可以是任意实数,单项式,多项式,但必须完全相同才能直接用法则。
例题讲解
观察下列各式,判断是否能用法则计算?
问题1:式子是否能直接利用法则计算?
当底数互为相反数时,根据乘方的意义,先转化为同底数幂形式.
问题2:遇到底数互为相反数时,如何解决?
不能,底数不同
课堂练习
计算下列各式,并用幂的形式表示结果.
(1) (-5)2 × (-5)3 × 54 (2) (a-b)2(b-a)
(2) (a-b)2(b-a)= (b-a)2(b-a)= (b-a)2+1=(b-a)3
互为相反数的偶数次幂相等x2n=(-x)2n
负数的奇数次幂为负
负数的偶数次幂为正
当底数互为相反数时,根据乘方的意义,先转化为同底数幂形式.
观察底数,指数,当指数为偶数时,利用互为相反数的偶数次幂相等进行转化为同底数幂。
(1) (-5)2 × (-5)3 × 54 = (-5)2 × (-5)3 × (-5)4 = (-5)2+3+4 =(-5)9 = -59
(-5)2 × (-5)3 × 54 = 52 × (-53) × 54 = -52+3+4 =-59
(a-b)2(b-a)= (a-b)2[-(a-b)]= -(a-b)2+1=-(a-b)3
课堂练习
下面的计算对吗?如果不对,应怎样改正?
底数不变,指数相加
合并同类项,系数相加
要发挥每个指数的作用
负数的偶数次幂为正
书本61页课内练习2
底数不变,指数相加
法则运用的条件:①同底数幂 ②乘法
课堂练习
底数的符号
积的符号
请你找找这两个式子的不同之处,并判断这两个式子的计算是否正确
注意准确地把握符号
①
②
课堂练习
例2:我国“神威·太湖之光”超级计算机的实测运算速度达到每秒9.3亿亿次。如果按这个速度工作一整天,那么它能运算多少次?
解
乘法的交换律和结合律
答:它一天约能运算
例题讲解
∵am · an = am+n (当m、n都是正整数)
∴ am+n=am · an (当m、n都是正整数)
逆用同底数幂乘法法则
若am+n=6,am=3,则an=
2
拓展提升
计算下列各式,结果用幂的形式表示.
注意:综合运算先乘法再加减,能合并同类项的要合并。
拓展提升
(A) 1对 (B) 2对 (C) 3对 (D) 4对
由同底数幂的乘法法则可知:x+y=5
拓展提升
填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x+1,则 x = .
3
5
5
23
23
3
25
36
22
×
=
33
32
×
×
=
转化思想
方程思想
拓展提升
今天,我们发现、归纳并应用了一个新的法则。法则的内容是什么?
经历了“观察--猜想--验证--概括”的过程,体现了从特殊到一般的归纳方法。
在运用法则的过程中要注意什么?
同底数幂的乘法法则:
am · an = am+n (m、n都是正整数)
同底数幂相乘,底数不变,指数相加
我们是怎么发现和归纳这个法则的 ?
同底数幂
乘法
条件:
底数互为相反数
转化
课堂总结
完成作业本(1)3.1同底数幂的乘法(1)
作业布置
https://www.21cnjy.com/help/help_extract.php
3.1同底数幂的乘法(1)
第1课时
浙教版 七年级下
指数
底数
幂
an 表示的意义是什么?其中a、n、an分别叫做什么
an表示n个相同因数a相乘的积。
这种求几个相同因数积的运算叫做乘方,乘方的结果叫幂。
旧知回顾
(1)25 表示________________;
(2)10×10×10×10写成幂的形式____;
(3) a的底数是__,指数是__;
(4) (a+b)3 的底数是______,指数是_____;
(5) (-2)4 的底数是___,指数是__;
(6) -24 的底数是___,指数是__.
2×2×2×2×2(5个2相乘)
104
a
1
a+b
3
-2
4
2
4
幂的底数是分数、负数或者多项式时,底数应该添加括号。
-24表示24的相反数
填空:
同底数幂是指底数相同的幂
不是
旧知回顾
根据乘方的意义,以及有理数的乘法,请完成下列问题:
(1) 是多少个2相乘?
(2) ( ) ( )
=
(3) ( ) ( )
=
5
3
2
7
2
5
7
4
3
思考:通过对以上过程的观察,你能发现什么规律吗?
猜想:am · an = (m、n都是正整数)
能用一个式子来表达这个规律吗?
用字母来表示一般规律
新知导入
猜想: am · an= (m、n都是正整数)
am · an =
m个a
n个a
= a·a·····a
=am+n
(m+n)个a
即:
am · an = am+n (m、n都是正整数)
(a·a·····a)
am+n
(乘法结合律)
(乘方的意义)
(乘方的意义)
(a·a·····a)
你能解释猜想am · an=am+n正确吗?
回顾探究的过程,我们经历了怎样的过程?
经历“观察-猜想-验证-概括”的过程
利用乘方的意义推理说明
新知导入
am · an = am+n (m、n都是正整数)
同底数幂相乘,
想一想:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法法则:
请你尝试用文字概括这个结论。
如 43×45=
43+5
=48
朗读法则并思考运用法则的条件是什么?
同底数幂
乘法
条件:
底数不变
指数相加
结论:
新知讲解
am · an · ap 等于什么?
猜想:
am· an· ap = am+n+p (m、n、p都是正整数)
方法2
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
方法1
am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
当三个或三个以上同底数幂相乘时,同底数幂乘法法则同样适用
新知讲解
下列各式哪些是同底数幂的乘法
法则运用的条件:①同底数幂 ②乘法
课堂练习
例1 计算下列各式,结果用幂的形式表示.
(1)
(2)
(3)
(4)
问题:这些式子是否能直接利用法则计算?
满足“底数相同,乘法运算”可以直接用法则。运算后结果:底数不变,指数相加。
运算结果的底数一般应化为正数,负数的奇数次幂为负。负数的偶数次幂为正。
指数为1时可省略不写,在运算时不能丢。
底数a可以是任意实数,单项式,多项式,但必须完全相同才能直接用法则。
例题讲解
观察下列各式,判断是否能用法则计算?
问题1:式子是否能直接利用法则计算?
当底数互为相反数时,根据乘方的意义,先转化为同底数幂形式.
问题2:遇到底数互为相反数时,如何解决?
不能,底数不同
课堂练习
计算下列各式,并用幂的形式表示结果.
(1) (-5)2 × (-5)3 × 54 (2) (a-b)2(b-a)
(2) (a-b)2(b-a)= (b-a)2(b-a)= (b-a)2+1=(b-a)3
互为相反数的偶数次幂相等x2n=(-x)2n
负数的奇数次幂为负
负数的偶数次幂为正
当底数互为相反数时,根据乘方的意义,先转化为同底数幂形式.
观察底数,指数,当指数为偶数时,利用互为相反数的偶数次幂相等进行转化为同底数幂。
(1) (-5)2 × (-5)3 × 54 = (-5)2 × (-5)3 × (-5)4 = (-5)2+3+4 =(-5)9 = -59
(-5)2 × (-5)3 × 54 = 52 × (-53) × 54 = -52+3+4 =-59
(a-b)2(b-a)= (a-b)2[-(a-b)]= -(a-b)2+1=-(a-b)3
课堂练习
下面的计算对吗?如果不对,应怎样改正?
底数不变,指数相加
合并同类项,系数相加
要发挥每个指数的作用
负数的偶数次幂为正
书本61页课内练习2
底数不变,指数相加
法则运用的条件:①同底数幂 ②乘法
课堂练习
底数的符号
积的符号
请你找找这两个式子的不同之处,并判断这两个式子的计算是否正确
注意准确地把握符号
①
②
课堂练习
例2:我国“神威·太湖之光”超级计算机的实测运算速度达到每秒9.3亿亿次。如果按这个速度工作一整天,那么它能运算多少次?
解
乘法的交换律和结合律
答:它一天约能运算
例题讲解
∵am · an = am+n (当m、n都是正整数)
∴ am+n=am · an (当m、n都是正整数)
逆用同底数幂乘法法则
若am+n=6,am=3,则an=
2
拓展提升
计算下列各式,结果用幂的形式表示.
注意:综合运算先乘法再加减,能合并同类项的要合并。
拓展提升
(A) 1对 (B) 2对 (C) 3对 (D) 4对
由同底数幂的乘法法则可知:x+y=5
拓展提升
填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x+1,则 x = .
3
5
5
23
23
3
25
36
22
×
=
33
32
×
×
=
转化思想
方程思想
拓展提升
今天,我们发现、归纳并应用了一个新的法则。法则的内容是什么?
经历了“观察--猜想--验证--概括”的过程,体现了从特殊到一般的归纳方法。
在运用法则的过程中要注意什么?
同底数幂的乘法法则:
am · an = am+n (m、n都是正整数)
同底数幂相乘,底数不变,指数相加
我们是怎么发现和归纳这个法则的 ?
同底数幂
乘法
条件:
底数互为相反数
转化
课堂总结
完成作业本(1)3.1同底数幂的乘法(1)
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
