3.1同底数幂的乘法(第2课时) 课件(20张ppt)
文档属性
| 名称 | 3.1同底数幂的乘法(第2课时) 课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-08 11:58:40 | ||
图片预览








文档简介
(共20张PPT)
3.1同底数幂的乘法
第2课时
浙教版 七年级下
1.同底数幂的乘法法则:
文字:同底数幂相乘,底数不变,指数相加.
公式:
指数相加
底数不变
am · an = am+n
旧知回顾
2.请同学们比较下列各组数的大小:
(1) ____ 0
(2) ____0
(3) ____ 0
(4) ____0
负数的偶次幂为正,奇次幂为负.
(6) ____
(5) ____
>
<
>
<
=
=
相反数的偶次幂相等.
旧知回顾
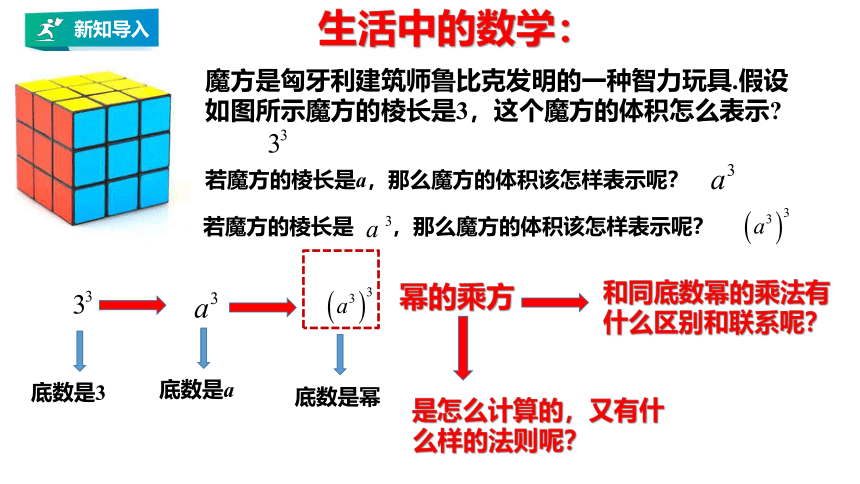
生活中的数学:
魔方是匈牙利建筑师鲁比克发明的一种智力玩具.假设如图所示魔方的棱长是3,这个魔方的体积怎么表示
若魔方的棱长是a,那么魔方的体积该怎样表示呢?
若魔方的棱长是 ,那么魔方的体积该怎样表示呢?
底数是3
底数是a
底数是幂
幂的乘方
是怎么计算的,又有什么样的法则呢?
和同底数幂的乘法有什么区别和联系呢?
新知导入
探究一:
1.请你根据乘方的意义填空
表示有____个____相乘
表示有____个____相乘
表示有____个____相乘
表示有____个____相乘
4
3
4
4
a
4
新知探究
探究二:
2.请你根据同底数幂的乘法、乘方的意义填空
=____=_____________=_______=____=___
=_____________=_________=____=____
同底数幂的乘法
幂的意义
=_______________=_________=____
归纳:你觉得幂的乘方运算有什么规律?你能用字母来表示吗?
新知探究
幂的乘方法则:
文字:幂的乘方,底数不变,指数相乘.
公式:
规律验证:
(幂的意义)
(同底数幂的乘法)
思考: 、 相等吗?
规律猜想:
新知探究
例3:计算下列各式,结果用幂的形式表示.
(1)
(2)
(3)
(4)
解:
(1)
(2)
(3)
(4)
(1)观察是否是幂的乘方,若是则根据法则计算.
(2)确定符号,负数的偶次幂为正,奇次幂为负.
(3)运算顺序,先是幂的乘方,再是幂的乘法.
例题讲解
1.(口答)计算下列各式,结果用幂的形式表示.
(1)
(2)
(3)
(4)
2.下面的计算对吗?如果不对,应该怎么样改正?
(1)
(2)
(3)
(4)
底数分别是什么?
负数的奇次幂为负,偶数次幂为正
课堂练习
对比学习:
同底数幂的乘法
(am)n=anm
指数相乘
底数不变
幂的乘方
相同点:
底数不变
底数不变
不同点:
指数相加
指数相乘
多个幂相乘
一个幂的乘方
指数相加
底数不变
am · an = am+n
新知巩固
3.计算下列各式,并用幂的形式表示结果.
(1)
(2)
(3)
解:
(1)
(2)
(3)
可以看成什么
课堂练习
4.计算下列各式,并用幂的形式表示结果.
(1)
(2)
(3)
解:
(1)
课堂练习
(2)
(3)
解:
原式
原式
解:
一定要同底数
课堂练习
幂的乘方公式:
公式逆用:
计算1:
若 ,则
计算2:
若 ,则
同底数幂的乘法公式:
拓展提升
计算1:
若 ,则
计算2:
若 ,则
思考: 和 有什么关系?
拓展提升
比较 这三个数的大小.
比一比:
比一比:
比较 这三个数的大小.
1.两数作差和0比
2.两数作商和1比
3.比倒数
4.用1减
拓展提升
幂的乘方
法则
底数不变指数相乘
联系
幂的乘方运算包含了同底数幂的乘法运算
逆运算
区别
指数相乘
课堂总结
完成作业本3.1幂的乘方(2)
作业布置
https://www.21cnjy.com/help/help_extract.php
3.1同底数幂的乘法
第2课时
浙教版 七年级下
1.同底数幂的乘法法则:
文字:同底数幂相乘,底数不变,指数相加.
公式:
指数相加
底数不变
am · an = am+n
旧知回顾
2.请同学们比较下列各组数的大小:
(1) ____ 0
(2) ____0
(3) ____ 0
(4) ____0
负数的偶次幂为正,奇次幂为负.
(6) ____
(5) ____
>
<
>
<
=
=
相反数的偶次幂相等.
旧知回顾
生活中的数学:
魔方是匈牙利建筑师鲁比克发明的一种智力玩具.假设如图所示魔方的棱长是3,这个魔方的体积怎么表示
若魔方的棱长是a,那么魔方的体积该怎样表示呢?
若魔方的棱长是 ,那么魔方的体积该怎样表示呢?
底数是3
底数是a
底数是幂
幂的乘方
是怎么计算的,又有什么样的法则呢?
和同底数幂的乘法有什么区别和联系呢?
新知导入
探究一:
1.请你根据乘方的意义填空
表示有____个____相乘
表示有____个____相乘
表示有____个____相乘
表示有____个____相乘
4
3
4
4
a
4
新知探究
探究二:
2.请你根据同底数幂的乘法、乘方的意义填空
=____=_____________=_______=____=___
=_____________=_________=____=____
同底数幂的乘法
幂的意义
=_______________=_________=____
归纳:你觉得幂的乘方运算有什么规律?你能用字母来表示吗?
新知探究
幂的乘方法则:
文字:幂的乘方,底数不变,指数相乘.
公式:
规律验证:
(幂的意义)
(同底数幂的乘法)
思考: 、 相等吗?
规律猜想:
新知探究
例3:计算下列各式,结果用幂的形式表示.
(1)
(2)
(3)
(4)
解:
(1)
(2)
(3)
(4)
(1)观察是否是幂的乘方,若是则根据法则计算.
(2)确定符号,负数的偶次幂为正,奇次幂为负.
(3)运算顺序,先是幂的乘方,再是幂的乘法.
例题讲解
1.(口答)计算下列各式,结果用幂的形式表示.
(1)
(2)
(3)
(4)
2.下面的计算对吗?如果不对,应该怎么样改正?
(1)
(2)
(3)
(4)
底数分别是什么?
负数的奇次幂为负,偶数次幂为正
课堂练习
对比学习:
同底数幂的乘法
(am)n=anm
指数相乘
底数不变
幂的乘方
相同点:
底数不变
底数不变
不同点:
指数相加
指数相乘
多个幂相乘
一个幂的乘方
指数相加
底数不变
am · an = am+n
新知巩固
3.计算下列各式,并用幂的形式表示结果.
(1)
(2)
(3)
解:
(1)
(2)
(3)
可以看成什么
课堂练习
4.计算下列各式,并用幂的形式表示结果.
(1)
(2)
(3)
解:
(1)
课堂练习
(2)
(3)
解:
原式
原式
解:
一定要同底数
课堂练习
幂的乘方公式:
公式逆用:
计算1:
若 ,则
计算2:
若 ,则
同底数幂的乘法公式:
拓展提升
计算1:
若 ,则
计算2:
若 ,则
思考: 和 有什么关系?
拓展提升
比较 这三个数的大小.
比一比:
比一比:
比较 这三个数的大小.
1.两数作差和0比
2.两数作商和1比
3.比倒数
4.用1减
拓展提升
幂的乘方
法则
底数不变指数相乘
联系
幂的乘方运算包含了同底数幂的乘法运算
逆运算
区别
指数相乘
课堂总结
完成作业本3.1幂的乘方(2)
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
