3.1 同底数幂的乘法(3) 课件(共16张PPT)
文档属性
| 名称 | 3.1 同底数幂的乘法(3) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-24 13:56:01 | ||
图片预览






文档简介
(共16张PPT)
3.1 同底数幂的乘法(3)
浙教版 七年级下册
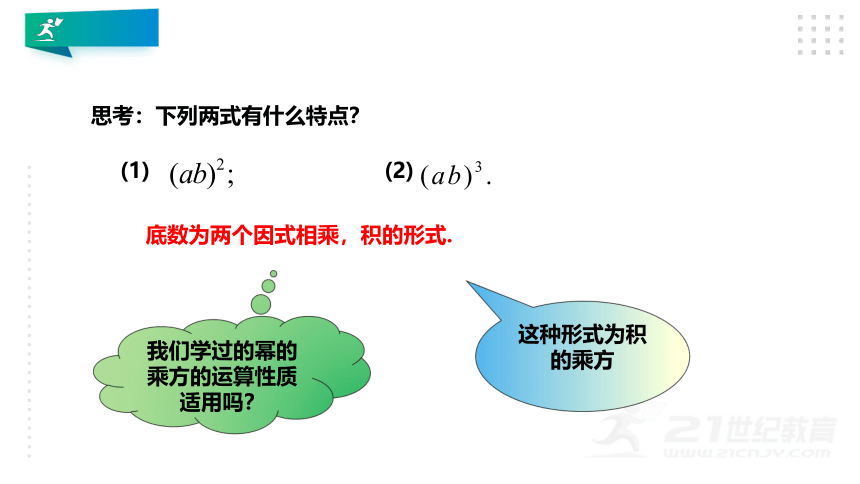
思考:下列两式有什么特点?
(1)
(2)
底数为两个因式相乘,积的形式.
这种形式为积的乘方
我们学过的幂的乘方的运算性质适用吗?
根据乘方的意义和同底数幂的乘法法则填空:
(1)(4×6)3 =(4×6)·(4×6)·(4×6)
=(4×4×4)·(6×6×6)
=4( ) ×6 ( ) .
(2)(4×6)5 =____________________________________
=4( ) ×6 ( ) .
(3)(ab)4 =____________________________________
=a( ) ×b ( ) .
3 3
(4×4×4×4×4)·(6×6×6×6×6)
5 5
(a×a×a×a)·(b×b×b×b)
4 4
你能归纳出积的乘方法则吗?
证明:
个
个
个
(n是正整数)
猜想:积的乘方(ab)n = anbn (n为正整数)
语言表述:
积的乘方法则
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
几何语言:
解:(1)(2b)5 =25 b5 =32b5 .
(2)(3x3)6 =3 6(x3)6 =36x18 =729x18 .
(3)(-x3 y2)3 =-(x3)3(y2 )3 =-x9 y6 .
(4) ( ab)4 =()4 a4 b4 =a4 b4 .
新知讲解
例4 计算下列各式:
(1)(2b)5 . (2)(3x 3 )6 .
(3)(-x3 y2 )3 . (4) (ab)4 .
合作探究
例5 木星是太阳系八大行星中最大的一颗. 木星可以近似地看做球体,它的半径大约是7×104km. 求木星的体积(结果精确到1014 位).
解:V = π×(7×10 4 )3=π×73 ×1012
≈ 1.44×1015 (km3 ).
答:木星的体积大约是 1.44×1015 km3
想一想:1.三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
2.积的乘方法则的逆用:
anbn = (ab)n (n为正整数)
解:原式
如何简便计算:
=4
D
A
解:原式=16x2.
解:原式=27x6.
解:原式=-a9b6.
解:(1)原式=8x6-x6=7x6.
(2)原式=-a3nb2n-a3nb2n=-2a3nb2n.
解:∵2x+3×3x+3=(2×3)x+3=6x+3,
36x-2=(62)x-2=62x-4,
2x+3×3x+3=36x-2,
∴x+3=2x-4,解得x=7.
6.如果(an·bm·b)3=a9b15,求m,n的值.
(an)3·(bm)3·b3=a9b15,
a3n ·b3m·b3=a9b15 ,
a3n ·b3m+3=a9b15,
3n=9 ,3m+3=15,
n=3,m=4.
解:∵(an·bm·b)3=a9b15,
积的乘方
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
(abc)n = anbncn (n为正整数)
推广
法则的逆用
anbn = (ab)n (n为正整数)
法则
https://www.21cnjy.com/help/help_extract.php
3.1 同底数幂的乘法(3)
浙教版 七年级下册
思考:下列两式有什么特点?
(1)
(2)
底数为两个因式相乘,积的形式.
这种形式为积的乘方
我们学过的幂的乘方的运算性质适用吗?
根据乘方的意义和同底数幂的乘法法则填空:
(1)(4×6)3 =(4×6)·(4×6)·(4×6)
=(4×4×4)·(6×6×6)
=4( ) ×6 ( ) .
(2)(4×6)5 =____________________________________
=4( ) ×6 ( ) .
(3)(ab)4 =____________________________________
=a( ) ×b ( ) .
3 3
(4×4×4×4×4)·(6×6×6×6×6)
5 5
(a×a×a×a)·(b×b×b×b)
4 4
你能归纳出积的乘方法则吗?
证明:
个
个
个
(n是正整数)
猜想:积的乘方(ab)n = anbn (n为正整数)
语言表述:
积的乘方法则
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
几何语言:
解:(1)(2b)5 =25 b5 =32b5 .
(2)(3x3)6 =3 6(x3)6 =36x18 =729x18 .
(3)(-x3 y2)3 =-(x3)3(y2 )3 =-x9 y6 .
(4) ( ab)4 =()4 a4 b4 =a4 b4 .
新知讲解
例4 计算下列各式:
(1)(2b)5 . (2)(3x 3 )6 .
(3)(-x3 y2 )3 . (4) (ab)4 .
合作探究
例5 木星是太阳系八大行星中最大的一颗. 木星可以近似地看做球体,它的半径大约是7×104km. 求木星的体积(结果精确到1014 位).
解:V = π×(7×10 4 )3=π×73 ×1012
≈ 1.44×1015 (km3 ).
答:木星的体积大约是 1.44×1015 km3
想一想:1.三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
2.积的乘方法则的逆用:
anbn = (ab)n (n为正整数)
解:原式
如何简便计算:
=4
D
A
解:原式=16x2.
解:原式=27x6.
解:原式=-a9b6.
解:(1)原式=8x6-x6=7x6.
(2)原式=-a3nb2n-a3nb2n=-2a3nb2n.
解:∵2x+3×3x+3=(2×3)x+3=6x+3,
36x-2=(62)x-2=62x-4,
2x+3×3x+3=36x-2,
∴x+3=2x-4,解得x=7.
6.如果(an·bm·b)3=a9b15,求m,n的值.
(an)3·(bm)3·b3=a9b15,
a3n ·b3m·b3=a9b15 ,
a3n ·b3m+3=a9b15,
3n=9 ,3m+3=15,
n=3,m=4.
解:∵(an·bm·b)3=a9b15,
积的乘方
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
(abc)n = anbncn (n为正整数)
推广
法则的逆用
anbn = (ab)n (n为正整数)
法则
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
