3.3多项式的乘法(1) 课件(共18张PPT)
文档属性
| 名称 | 3.3多项式的乘法(1) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-11 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
3.3多项式的乘法
第1课时
浙教版 七年级下
新知导入
整式定义:单项式和多项式统称为整式
整式运算
整式的加减
整式的乘除
整式的乘法
同底数幂相乘、幂的乘方、积的乘方是整式乘法的基础
单项式乘单项式
单项式乘多项式
多项式乘多项式
整式的除法
知识结构
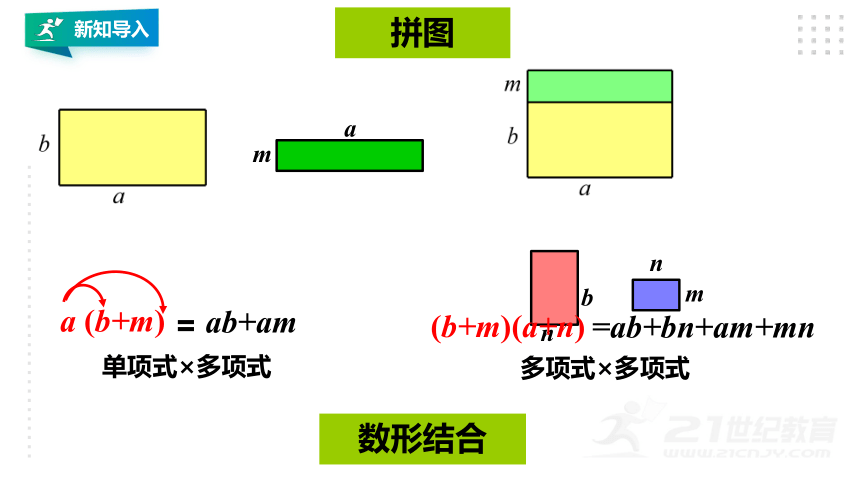
a
m
ab+am
a (b+m)
=
新知导入
n
b
n
m
(b+m)(a+n)
=ab+bn+am+mn
单项式×多项式
多项式×多项式
拼图
数形结合
新知讲解
设X=b+m,
则原式=(a+n)X=aX+nX
=a(b+m)+n(b+m)
=ab+am+nb+nm
代数推导法
(a+n)(b+m)
即(a+n)(b+m)
=ab+am+nb+nm
新知讲解
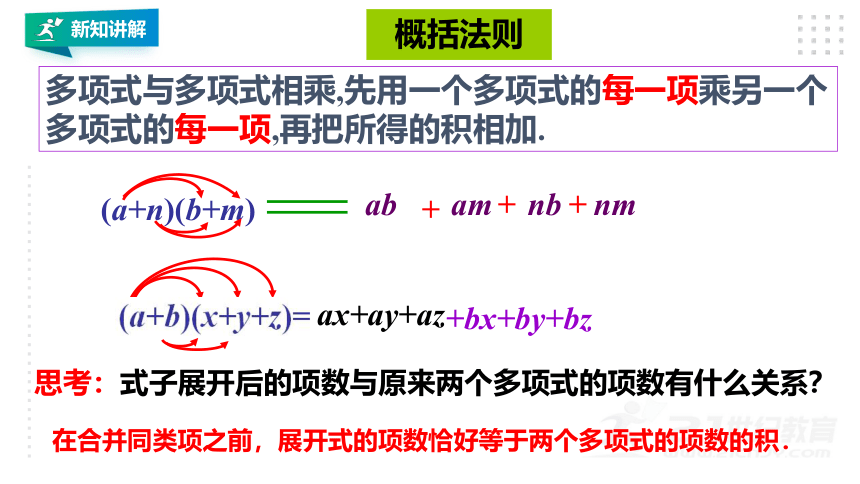
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
概括法则
思考:式子展开后的项数与原来两个多项式的项数有什么关系?
(a+n)(b+m)
ab
+
am
+
nb
+
nm
ax+ay+az
+bx+by+bz
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
例题讲解
例1 计算:
应用法则
(1)(x+y)(a+2b)
(2)(3x-1)(x+3)
= x · a+ x · (2b)+ y · a+ y ·(2b)
= a x + 2b x + a y + 2b y
=3x2+9x-x-3
=3x2+8x-3
(3) (x-y)(-a+2b)
(4)(-3x-1)(x-3)
课堂练习
(1)
(2)
(4)
感悟:多项式与多项式相乘过程中有哪些需要注意的地方?
(2a-b)2
(x+1)(x-1)
(2a-3)(3a+1)
计算:
(1)(x+1)(x-1)
= x2-x+x-1
=x2-1
(2)(2a-3)(3a+1)
= 6a2+2a-9a-3
= 6a2-7a-3
(4) (2a-b)2
= (2a-b) (2a-b)
=4a2-2ab-2ab+b2
(3)
(6a+1)(a-4)
(3) (6a+1)(a-4)
= 6a2-24a+a-4
= 6a2-23a-4
=4a2-4ab+b2
解:
课堂练习
(1)
(4)
(2)
(3)
-
例2
2
变式:
(2a-b)2
(6a+1)(a-4)
(x+1)(x-1)
(2a-3)(3a+1)
计算:
-
(
)
计算:
先化简,再求值:
当 时,原式=16× =1
解:原式=
6a2-7a-3
6a2-23a-4
=6a2-7a-3-6a2+23a+4
=16a+1
感悟:多项式与多项式相乘过程中有哪些需要注意的地方?
课堂练习
先化简,再求值:
-5x(1-2x)-(x+1)(10x-2),其中
课堂练习
一幅宣传画的长为a(cm),宽为b(cm),把它贴在一块长方形木板上,四周刚好留出2cm的边框宽,请你算一算这块木板的面积是多少
a
b
2
解:(a+4)(b+4)
=ab+4a+4b+16
拓展提升
计算:
①(x+2)(x+3)
②(x+4)(x 2)
③(x-3)(x 4)
=x2 + 5x +6
(2)你能很快说出与(x+a)(x+b)相等的多项式吗?
(x+a)(x+b)= x2+(a+b)x +ab
=x2 +2x -8
=x2-7x +12
这三个式子是一种特殊的多项式乘以多项式,
请观察这三个式子有什么共同特点?你发现什么规律?
3
5
3
5
(1)按你发现的规律填空:
(x+3)(x+5)=x2+(___+___)x+____×___
相同字母的平方(x2);
两个常数的和
两个常数的积.
(x+a)(x+b)=x2+(a+b)x+ab
(3)根据(2)中结论计算:
①(x+1)(x+2)=
②(x+1)(x-2)=
③(x-1)(x+2)=
④(x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
拓展提升
变式1:若(x+m)(x-2)=x2+nx-6对x的任何值都成立,则m=_____,n=_____
变式2:若(x+m)(x-2)不含x的一次项,则m=_____
3
1
2
拓展提升
如图,有正方形卡片A,B和长方形卡片C若干张.若要拼一个长为(a+2b)、宽为(a+b)的大长方形,则需要C类卡片_______张.
拓展提升
课堂总结
(a+n)(b+m)
a(b+m)+n(b+m)
ab+am+nb+nm
=
=
分配律
分配律
多项式×
多项式
单项式×
多项式
单项式×
单项式
1
1
2
2
3
3
4
4
1.你对多项式的运算法则是怎么理解的?
2.多项式的乘法要注意哪些方面?
3.这节课你用到了哪些数学思想方法.
作业布置
作业本3.3(1)
https://www.21cnjy.com/help/help_extract.php
3.3多项式的乘法
第1课时
浙教版 七年级下
新知导入
整式定义:单项式和多项式统称为整式
整式运算
整式的加减
整式的乘除
整式的乘法
同底数幂相乘、幂的乘方、积的乘方是整式乘法的基础
单项式乘单项式
单项式乘多项式
多项式乘多项式
整式的除法
知识结构
a
m
ab+am
a (b+m)
=
新知导入
n
b
n
m
(b+m)(a+n)
=ab+bn+am+mn
单项式×多项式
多项式×多项式
拼图
数形结合
新知讲解
设X=b+m,
则原式=(a+n)X=aX+nX
=a(b+m)+n(b+m)
=ab+am+nb+nm
代数推导法
(a+n)(b+m)
即(a+n)(b+m)
=ab+am+nb+nm
新知讲解
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
概括法则
思考:式子展开后的项数与原来两个多项式的项数有什么关系?
(a+n)(b+m)
ab
+
am
+
nb
+
nm
ax+ay+az
+bx+by+bz
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
例题讲解
例1 计算:
应用法则
(1)(x+y)(a+2b)
(2)(3x-1)(x+3)
= x · a+ x · (2b)+ y · a+ y ·(2b)
= a x + 2b x + a y + 2b y
=3x2+9x-x-3
=3x2+8x-3
(3) (x-y)(-a+2b)
(4)(-3x-1)(x-3)
课堂练习
(1)
(2)
(4)
感悟:多项式与多项式相乘过程中有哪些需要注意的地方?
(2a-b)2
(x+1)(x-1)
(2a-3)(3a+1)
计算:
(1)(x+1)(x-1)
= x2-x+x-1
=x2-1
(2)(2a-3)(3a+1)
= 6a2+2a-9a-3
= 6a2-7a-3
(4) (2a-b)2
= (2a-b) (2a-b)
=4a2-2ab-2ab+b2
(3)
(6a+1)(a-4)
(3) (6a+1)(a-4)
= 6a2-24a+a-4
= 6a2-23a-4
=4a2-4ab+b2
解:
课堂练习
(1)
(4)
(2)
(3)
-
例2
2
变式:
(2a-b)2
(6a+1)(a-4)
(x+1)(x-1)
(2a-3)(3a+1)
计算:
-
(
)
计算:
先化简,再求值:
当 时,原式=16× =1
解:原式=
6a2-7a-3
6a2-23a-4
=6a2-7a-3-6a2+23a+4
=16a+1
感悟:多项式与多项式相乘过程中有哪些需要注意的地方?
课堂练习
先化简,再求值:
-5x(1-2x)-(x+1)(10x-2),其中
课堂练习
一幅宣传画的长为a(cm),宽为b(cm),把它贴在一块长方形木板上,四周刚好留出2cm的边框宽,请你算一算这块木板的面积是多少
a
b
2
解:(a+4)(b+4)
=ab+4a+4b+16
拓展提升
计算:
①(x+2)(x+3)
②(x+4)(x 2)
③(x-3)(x 4)
=x2 + 5x +6
(2)你能很快说出与(x+a)(x+b)相等的多项式吗?
(x+a)(x+b)= x2+(a+b)x +ab
=x2 +2x -8
=x2-7x +12
这三个式子是一种特殊的多项式乘以多项式,
请观察这三个式子有什么共同特点?你发现什么规律?
3
5
3
5
(1)按你发现的规律填空:
(x+3)(x+5)=x2+(___+___)x+____×___
相同字母的平方(x2);
两个常数的和
两个常数的积.
(x+a)(x+b)=x2+(a+b)x+ab
(3)根据(2)中结论计算:
①(x+1)(x+2)=
②(x+1)(x-2)=
③(x-1)(x+2)=
④(x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
拓展提升
变式1:若(x+m)(x-2)=x2+nx-6对x的任何值都成立,则m=_____,n=_____
变式2:若(x+m)(x-2)不含x的一次项,则m=_____
3
1
2
拓展提升
如图,有正方形卡片A,B和长方形卡片C若干张.若要拼一个长为(a+2b)、宽为(a+b)的大长方形,则需要C类卡片_______张.
拓展提升
课堂总结
(a+n)(b+m)
a(b+m)+n(b+m)
ab+am+nb+nm
=
=
分配律
分配律
多项式×
多项式
单项式×
多项式
单项式×
单项式
1
1
2
2
3
3
4
4
1.你对多项式的运算法则是怎么理解的?
2.多项式的乘法要注意哪些方面?
3.这节课你用到了哪些数学思想方法.
作业布置
作业本3.3(1)
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
