第一章 平行线 章末复习 课件(共27张PPT)
文档属性
| 名称 | 第一章 平行线 章末复习 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:22:52 | ||
图片预览







文档简介
(共27张PPT)
第一章 平行线
章末复习课件
浙教版 七年级下册
知识梳理
Part 1
知识梳理
1.概念:在同一平面内,不相交的两条直线叫做平行线,
平行用符号“∥”表示,
如:直线与直线互相平行,记作∥,读作a平行于b。
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合
2.画法:一落、二靠、三移、四画。
知识点1 平行线
3.平行公理(唯一性):
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论(传递性):
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
几何描述 :
∵b∥a,c∥a
∴b∥c
知识梳理
【例1】下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
A
【例2】如图,过C点作线段AB的平行线,说法正确的是( )
A.不能作 B.只能作一条
C.能作两条 D.能作无数条
B
巩固练习
同位角:在两条直线的上方,又在第三条直线的同侧,具有这种位置关系的两个角叫同位角。(同旁同侧)
如:∠1和∠5。
内错角:在在两条直线之间,又在第三条直线的两侧,具有这种位置关系的两个角叫内错角。(内部异侧)
如:∠3和∠5。
同旁内角:在在两条直线之间,又在第三条直线的同侧,具有这种位置关系的两个角叫同旁内角。(同旁内侧)
如:∠3和∠6。
知识点2 同位角、内错角与同旁内角
知识梳理
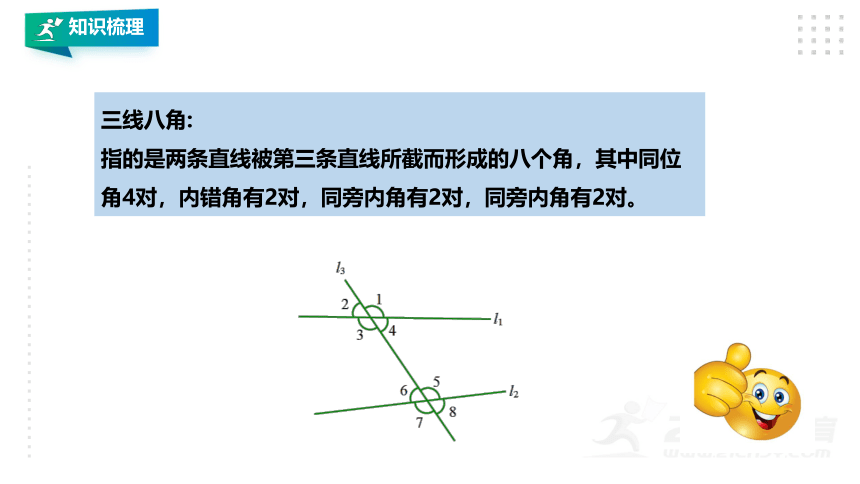
三线八角:
指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对,同旁内角有2对。
知识梳理
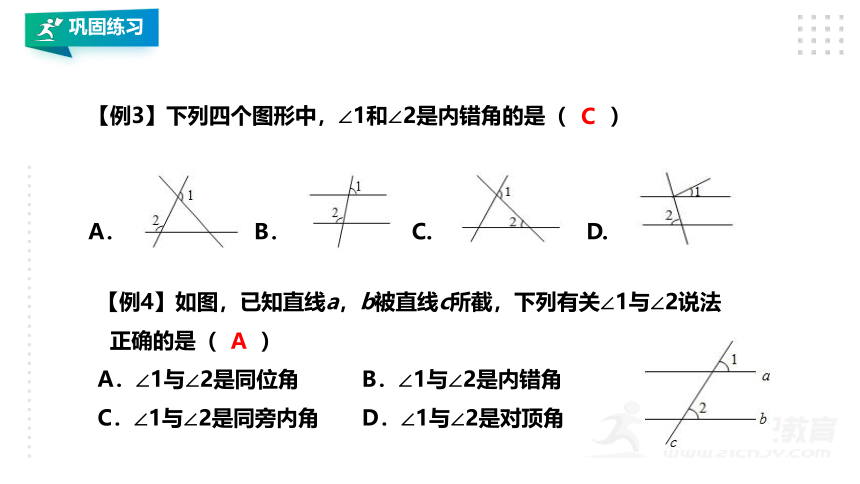
【例3】下列四个图形中,∠1和∠2是内错角的是( )
A. B. C. D.
C
【例4】如图,已知直线a,b被直线c所截,下列有关∠1与∠2说法正确的是( )
A.∠1与∠2是同位角 B.∠1与∠2是内错角
C.∠1与∠2是同旁内角 D.∠1与∠2是对顶角
A
巩固练习
判定方法 1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行
判定方法 2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行
判定方法 3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行
知识点3 平行线的判定
知识梳理
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
知识梳理
根据平行线的定义和平行公理的推论,平行线的判定方法还有:
(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.
(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).
(3)在同一平面内,垂直于同一直线的两条直线平行.
(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
知识梳理
【例5】如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠3=180°
C.∠1=∠4 D.∠1+∠4=180°
C
【例6】有下列说法:①对顶角相等;②内错角相等;③平面内过一点有且只有一条直线垂直于已知直线;④平面内过一点有且只有一条直线平行于已知直线,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
B
巩固练习
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
知识点4 平行线的性质
知识梳理
根据平行线的定义和平行公理的推论,平行线的性质还有:
(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.
(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.
知识梳理
【例7】如图,如果∠1=∠3,∠2=50°,那么∠4的度数为( )
A.50° B.100° C.120° D.130°
D
【例8】如图,已知AE交CD于点O,AB∥CD,∠A=50°,∠E=15°,则∠C的度数为( )
A.50° B.65° C.35° D.15°
C
巩固练习
知识点5 图形的平移
1.平移的概念:
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移变换 (简称平移),平移不改变物体的形状和大小。
(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
(2)新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点
(3)连接各组对应点的线段平行且相等。
2.平移的性质:
知识梳理
作平移图形的一般步骤:
1、确定平移的方向和距离。
2、确定图形的关键点。
3、过这些关键点作与平移方向平行的射线,在射线上截取与平移的距离相等的线段,得到关键点的对应点。
4、依次连接关键点,作出平移后的新图形。
知识梳理
【例9】2022年,中国将举办第二十四届冬季奥林匹克运动会,如图,通过平移吉祥物“冰墩墩”可以得到的图形是( )
A. B. C. D.
B
巩固练习
提升训练
Part 2
练习1:下列生活实例中;①交通道口的斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车的平直铁轨线.其中属于平行线的有( )
A.1个 B.2个 C.3个 D.4个
D
练习2:下列表示方法正确的是( )
A.a∥A B.AB∥cd C.A∥B D.a∥b
D
提升训练
练习3:如图,下列说法不正确的是( )
A.∠1与∠3是对顶角 B.∠2与∠6是同位角
C.∠3与∠4是内错角 D.∠3与∠5是同旁内角
B
练习4:如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 (填序号).
①②③
提升训练
练习5:如图所示,已知直线c与a,b分别交于点A、B且∠1=120°,当∠2=( )时,直线a∥b.
A.60° B.120° C.30° D.150°
B
练习6:如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.能判定AB∥CD的条件为 .
①③④
提升训练
练习7:如图,把长方形ABCD沿EF对折,若∠1=44°,则∠AEF等于( )
A.136° B.102° C.122° D.112°
D
练习8:一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FD∥AB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
B
提升训练
练习9:如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为( )
A.3 B.4 C.5 D.6
A
练习10:如图,将三角形ABC沿OM方向平移一定的距离得到三角形A′B′C′,则下列结论中不正确的是( )
A.AA′∥BB ′ B.AA'=BB '
C.∠ACB=∠A'B 'C ' D.BC=B 'C'
C
提升训练
练习11:如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.
解:DE∥BF,
理由是:∵∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,
∴∠1=∠ABF,
∵∠1=∠2,
∴∠2=∠ABF,
∴DE∥BF.
提升训练
练习12:如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9cm,DB=2cm.请求出CF的长度.
解:(1)∵在Rt△ABC中,∠C=90°,∠A=33°,
∴∠CBA=90°﹣33°=57°,
由平移得,∠E=∠CBA=57°;
(2)由平移得,AD=BE=CF,
∵AE=9cm,DB=2cm,
∴AD=BE=×(9﹣2)=3.5cm,
∴CF=3.5cm.
提升训练
https://www.21cnjy.com/help/help_extract.php
第一章 平行线
章末复习课件
浙教版 七年级下册
知识梳理
Part 1
知识梳理
1.概念:在同一平面内,不相交的两条直线叫做平行线,
平行用符号“∥”表示,
如:直线与直线互相平行,记作∥,读作a平行于b。
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合
2.画法:一落、二靠、三移、四画。
知识点1 平行线
3.平行公理(唯一性):
经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论(传递性):
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
几何描述 :
∵b∥a,c∥a
∴b∥c
知识梳理
【例1】下列说法不正确的是( )
A.过任意一点可作已知直线的一条平行线
B.同一平面内两条不相交的直线是平行线
C.在同一平面内,过直线外一点只能画一条直线与已知直线垂直
D.平行于同一直线的两直线平行
A
【例2】如图,过C点作线段AB的平行线,说法正确的是( )
A.不能作 B.只能作一条
C.能作两条 D.能作无数条
B
巩固练习
同位角:在两条直线的上方,又在第三条直线的同侧,具有这种位置关系的两个角叫同位角。(同旁同侧)
如:∠1和∠5。
内错角:在在两条直线之间,又在第三条直线的两侧,具有这种位置关系的两个角叫内错角。(内部异侧)
如:∠3和∠5。
同旁内角:在在两条直线之间,又在第三条直线的同侧,具有这种位置关系的两个角叫同旁内角。(同旁内侧)
如:∠3和∠6。
知识点2 同位角、内错角与同旁内角
知识梳理
三线八角:
指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对,同旁内角有2对。
知识梳理
【例3】下列四个图形中,∠1和∠2是内错角的是( )
A. B. C. D.
C
【例4】如图,已知直线a,b被直线c所截,下列有关∠1与∠2说法正确的是( )
A.∠1与∠2是同位角 B.∠1与∠2是内错角
C.∠1与∠2是同旁内角 D.∠1与∠2是对顶角
A
巩固练习
判定方法 1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行
判定方法 2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行
判定方法 3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行
知识点3 平行线的判定
知识梳理
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
知识梳理
根据平行线的定义和平行公理的推论,平行线的判定方法还有:
(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.
(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).
(3)在同一平面内,垂直于同一直线的两条直线平行.
(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
知识梳理
【例5】如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠3=180°
C.∠1=∠4 D.∠1+∠4=180°
C
【例6】有下列说法:①对顶角相等;②内错角相等;③平面内过一点有且只有一条直线垂直于已知直线;④平面内过一点有且只有一条直线平行于已知直线,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
B
巩固练习
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
知识点4 平行线的性质
知识梳理
根据平行线的定义和平行公理的推论,平行线的性质还有:
(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.
(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.
知识梳理
【例7】如图,如果∠1=∠3,∠2=50°,那么∠4的度数为( )
A.50° B.100° C.120° D.130°
D
【例8】如图,已知AE交CD于点O,AB∥CD,∠A=50°,∠E=15°,则∠C的度数为( )
A.50° B.65° C.35° D.15°
C
巩固练习
知识点5 图形的平移
1.平移的概念:
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移变换 (简称平移),平移不改变物体的形状和大小。
(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
(2)新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点
(3)连接各组对应点的线段平行且相等。
2.平移的性质:
知识梳理
作平移图形的一般步骤:
1、确定平移的方向和距离。
2、确定图形的关键点。
3、过这些关键点作与平移方向平行的射线,在射线上截取与平移的距离相等的线段,得到关键点的对应点。
4、依次连接关键点,作出平移后的新图形。
知识梳理
【例9】2022年,中国将举办第二十四届冬季奥林匹克运动会,如图,通过平移吉祥物“冰墩墩”可以得到的图形是( )
A. B. C. D.
B
巩固练习
提升训练
Part 2
练习1:下列生活实例中;①交通道口的斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车的平直铁轨线.其中属于平行线的有( )
A.1个 B.2个 C.3个 D.4个
D
练习2:下列表示方法正确的是( )
A.a∥A B.AB∥cd C.A∥B D.a∥b
D
提升训练
练习3:如图,下列说法不正确的是( )
A.∠1与∠3是对顶角 B.∠2与∠6是同位角
C.∠3与∠4是内错角 D.∠3与∠5是同旁内角
B
练习4:如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是 (填序号).
①②③
提升训练
练习5:如图所示,已知直线c与a,b分别交于点A、B且∠1=120°,当∠2=( )时,直线a∥b.
A.60° B.120° C.30° D.150°
B
练习6:如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.能判定AB∥CD的条件为 .
①③④
提升训练
练习7:如图,把长方形ABCD沿EF对折,若∠1=44°,则∠AEF等于( )
A.136° B.102° C.122° D.112°
D
练习8:一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FD∥AB,∠B=30°,则∠ADB的度数是( )
A.95° B.105° C.115° D.125°
B
提升训练
练习9:如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为( )
A.3 B.4 C.5 D.6
A
练习10:如图,将三角形ABC沿OM方向平移一定的距离得到三角形A′B′C′,则下列结论中不正确的是( )
A.AA′∥BB ′ B.AA'=BB '
C.∠ACB=∠A'B 'C ' D.BC=B 'C'
C
提升训练
练习11:如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠1=∠2,试说明DE∥FB.
解:DE∥BF,
理由是:∵∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,
∴∠1=∠ABF,
∵∠1=∠2,
∴∠2=∠ABF,
∴DE∥BF.
提升训练
练习12:如图,在Rt△ABC中,∠C=90°,∠A=33°,将△ABC沿AB方向向右平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9cm,DB=2cm.请求出CF的长度.
解:(1)∵在Rt△ABC中,∠C=90°,∠A=33°,
∴∠CBA=90°﹣33°=57°,
由平移得,∠E=∠CBA=57°;
(2)由平移得,AD=BE=CF,
∵AE=9cm,DB=2cm,
∴AD=BE=×(9﹣2)=3.5cm,
∴CF=3.5cm.
提升训练
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
