2021-2022学年浙教版七年级数学下册第1章平行线单元综合测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册第1章平行线单元综合测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 329.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-13 11:36:55 | ||
图片预览

文档简介
2021-2022学年浙教版七年级数学下册《第1章平行线》单元综合测试题(附答案)
一.选择题(共8小题,满分40分)
1.下列说法:
①和为180°且有一条公共边的两个角是邻补角;
②过一点有且只有一条直线与已知直线垂直;
③同位角相等;
④经过直线外一点,有且只有一条直线与这条直线平行;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.如图,直线a,b,c被射线l和m所截,则下列关系正确的是( )
A.∠1与∠2是对顶角 B.∠1与∠3是同旁内角
C.∠3与∠4是同位角 D.∠2与∠3是内错角
3.如图,点E在AB的延长线上,下列条件中能够判断AD∥BC的是( )
A.∠1=∠3 B.∠C=∠CBE
C.∠C+∠ABC=180° D.∠2=∠4
4.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA=( )
A.20° B.40° C.50° D.60°
5.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )
A.30° B.60° C.30°或60° D.60°或120°
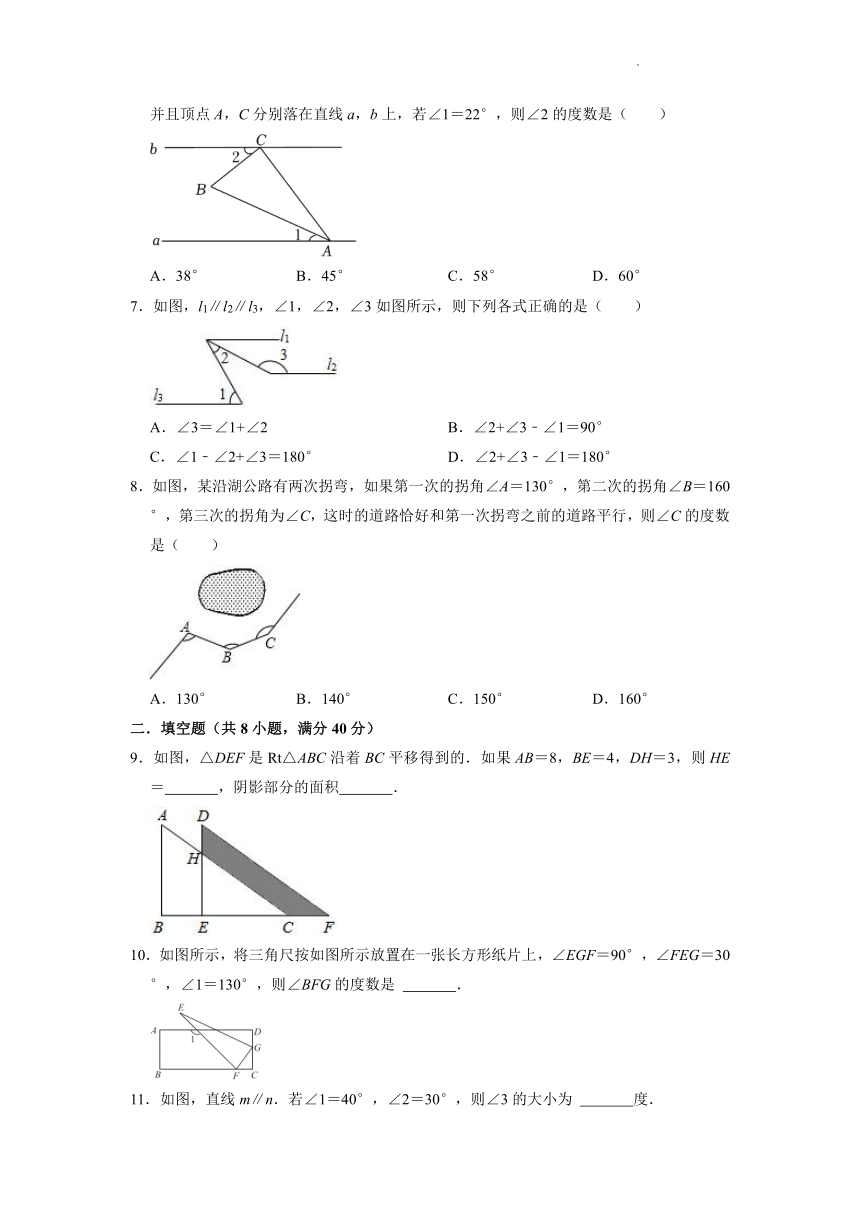
6.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
7.如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是( )
A.∠3=∠1+∠2 B.∠2+∠3﹣∠1=90°
C.∠1﹣∠2+∠3=180° D.∠2+∠3﹣∠1=180°
8.如图,某沿湖公路有两次拐弯,如果第一次的拐角∠A=130°,第二次的拐角∠B=160°,第三次的拐角为∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数是( )
A.130° B.140° C.150° D.160°
二.填空题(共8小题,满分40分)
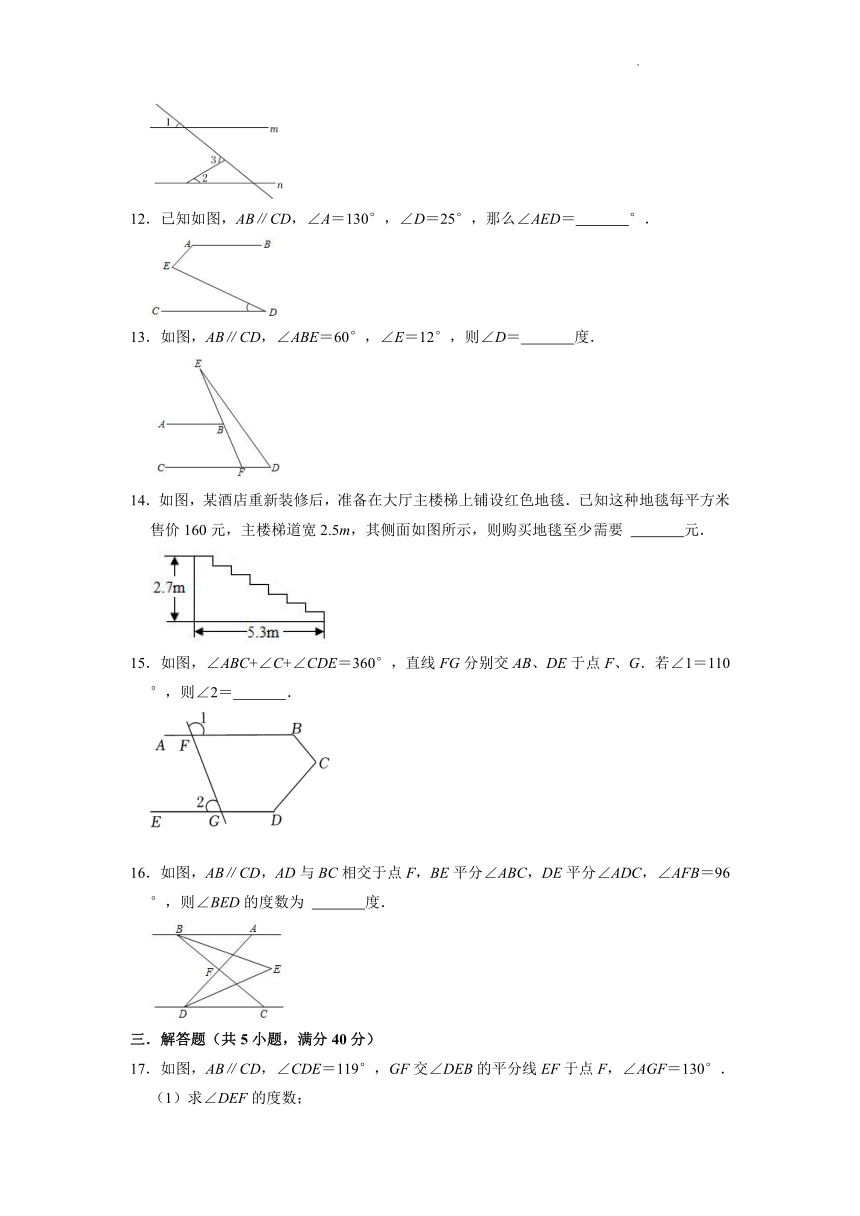
9.如图,△DEF是Rt△ABC沿着BC平移得到的.如果AB=8,BE=4,DH=3,则HE= ,阴影部分的面积 .
10.如图所示,将三角尺按如图所示放置在一张长方形纸片上,∠EGF=90°,∠FEG=30°,∠1=130°,则∠BFG的度数是 .
11.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为 度.
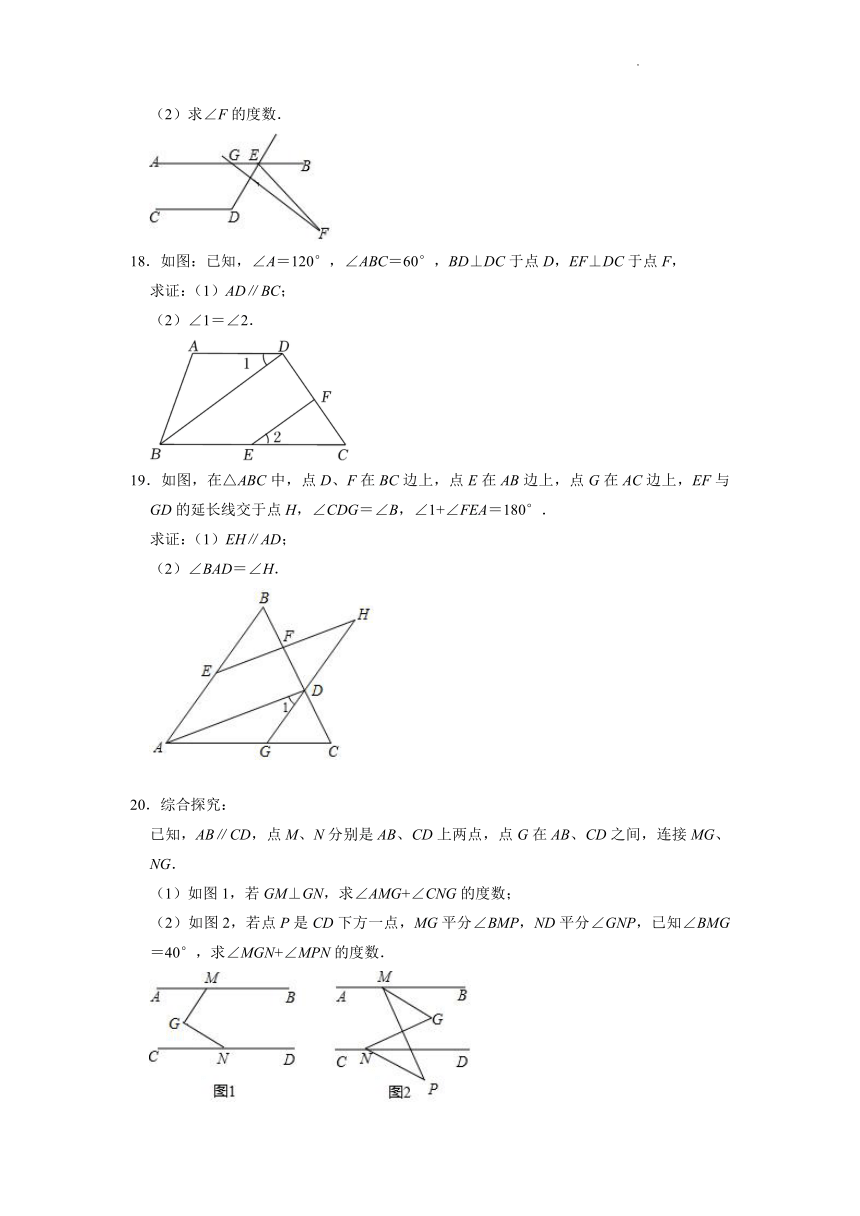
12.已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED= °.
13.如图,AB∥CD,∠ABE=60°,∠E=12°,则∠D= 度.
14.如图,某酒店重新装修后,准备在大厅主楼梯上铺设红色地毯.已知这种地毯每平方米售价160元,主楼梯道宽2.5m,其侧面如图所示,则购买地毯至少需要 元.
15.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=110°,则∠2= .
16.如图,AB∥CD,AD与BC相交于点F,BE平分∠ABC,DE平分∠ADC,∠AFB=96°,则∠BED的度数为 度.
三.解答题(共5小题,满分40分)
17.如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°.
(1)求∠DEF的度数;
(2)求∠F的度数.
18.如图:已知,∠A=120°,∠ABC=60°,BD⊥DC于点D,EF⊥DC于点F,
求证:(1)AD∥BC;
(2)∠1=∠2.
19.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
20.综合探究:
已知,AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=40°,求∠MGN+∠MPN的度数.
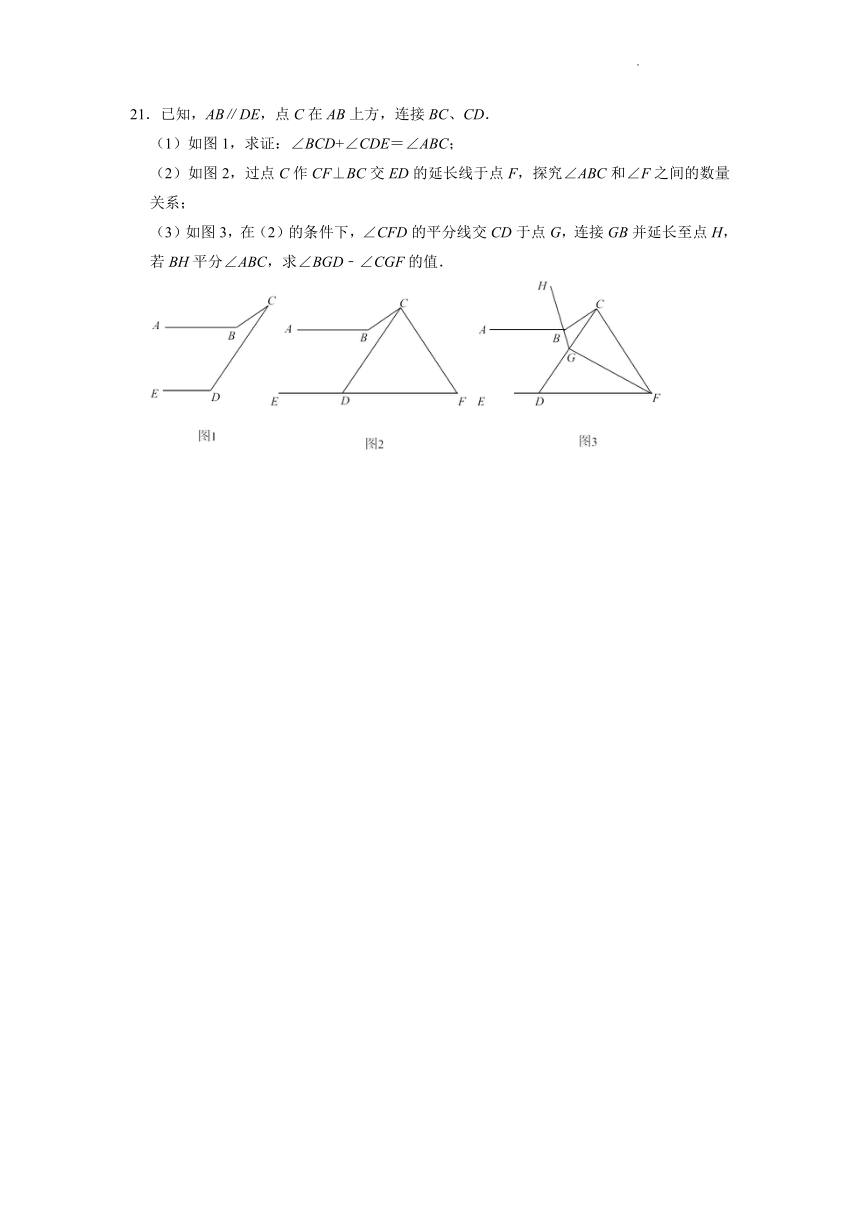
21.已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
参考答案
一.选择题(共8小题,满分40分)
1.解:①两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角,原说法错误,不符合题意;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;原说法错误,不符合题意;
③两直线平行,同位角相等;原说法错误,不符合题意;
④经过直线外一点,有且只有一条直线与这条直线平行;原说法正确,符合题意;
其中正确的有1个,
故选:B.
2.解:A、∠1与∠2不是对顶角,原说法错误,故此选项不符合题意;
B、∠1与∠3不是同旁内角,原说法错误,故此选项不符合题意;
C、∠3与∠4是同位角,原说法错误,故此选项不符合题意;
D、∠2与∠3不是内错角,原说法错误,故此选项不符合题意;
故选:C.
3.解:由∠2=∠4,可得AD∥CB;
由∠1=∠3或∠C=∠CBE或∠C+∠ABC=180°,可得AB∥DC;
故选:D.
4.解:由图可得,∠AEF=50°,
又∵DC∥EF,
∴∠BAC=50°,
∵∠B=30°,
∴∠BDA=50°﹣30°=20°,
故选:A.
5.解:如图1,
∵a∥b,
∴∠1=∠α,
∵c∥d,
∴∠β=∠1=∠α=60°;
如图(2),
∵a∥b,
∴∠α+∠2=180°,
∵c∥d,
∴∠2=∠β,
∴∠β+∠α=180°,
∵∠α=60°,
∴∠β=120°.
综上,∠β=60°或120°.
故选:D.
6.解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故选:A.
7.解:∵l1∥l2∥l3,
∴∠1=∠2+∠4,∠4+∠3=180°,
∴∠1﹣∠2+∠3=180°,
故选:C.
8.解:过点B作BE∥AD,
∵AD∥CF,
∴BE∥AD∥CF,
∴∠ABE=∠A=130°,∠EBC+∠C=180°,
∵∠ABC=160°,∠ABE+∠EBC=∠ABC,
∴∠EBC=30°,
∴∠C=150°.
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵Rt△ABC沿BC方向平移得到Rt△DEF,
∴AB=DE=8,S△ABC=S△DEF,
∴阴影部分面积=梯形ABEH的面积,
∵DH=3,
∴EH=8﹣3=5,
∴阴影部分面积=×(5+8)×4=26.
故答案为5,26.
10.解:∵AD∥BC,∠1=130°,
∴∠BFE=180°﹣∠1=50°,
又∵∠EGF=90°,∠FEG=30°,
∴∠EFG=60°,
∴∠BFG=50°+60°=110°,
故答案为:110°.
11.解:如图,
∵m∥n.∠1=40°,
∴∠4=∠1=40°,
∵∠3是图中三角形的外角,∠2=30°,
∴∠3=∠2+∠4=70°.
故答案为:70.
12.解:如图:过E作EF∥AB,则AB∥EF∥CD,
∵∠A=130°,
∴∠1=180°﹣130°=50°,
∵∠D=25°,
∴∠2=∠D=25°,
∴∠AED=50°+25°=75°,
故答案为:75.
13.解:过点E作EH∥AB,如图,
∵EH∥AB,
∴∠HEB+∠ABE=180°.
∵∠ABE=60°,
∴∠HEB=120°.
∴∠HED=∠HEB+∠FED=120°+12°=132°.
∵EH∥AB,AB∥CD,
∴HE∥CD.
∴∠HED+∠D=180°.
∴∠D=180°﹣132°=48°.
故答案为:48.
14.解:由题意得:
2.7+5.3=8(m),
8×2.5×160=3200(元),
∴购买地毯至少需要3200元,
故答案为:3200.
15.解:如图,过点C作CH∥AB,
则∠ABC+∠BCH=180°,
∵∠ABC+∠C+∠CDE=360°,即∠ABC+∠BCH+∠DCH+∠CDE=360°,
∴∠DCH+∠CDE=180°,
∴CH∥DE,
∴AB∥DE,
∴∠DGF=∠1=110°,
∴∠2=180°﹣110°=70°,
故答案为:70°.
16.解:如图,过点E作EP∥AB,
∵AB∥CD,
∴AB∥CD∥EP,
∴∠ABE=∠BEP,∠CDE=∠DEP,∠ABC=∠BCD,
∵∠ABC+∠BAD+∠AFB=180°,
∴∠ABC+∠BAD=180°﹣∠AFB=84°,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC,∠CDE=∠ADC,
∴∠ABE+∠CDE=(∠ABC+∠BAD)=42°,
∴∠BED=∠BEP+∠DEP=∠ABE+∠CDE)=42°,
故答案为:42.
三.解答题(共5小题,满分40分)
17.解:(1)∵AB∥CD,∠CDE=119°,
∴∠CDE=∠BED=119°,
∵EF平分∠BED,
∴∠DEF=∠BED=59.5°;
答:∠DEF的度数为59.5°.
(2)∵∠AGF=130°,
∴∠FGB=50°,
由(1)知,∠DEF=59.5°,
∵EF平分∠BED,
∴∠DEF=∠BEF=59.5°,
又∵∠BEF=∠FGB+∠F,
∴∠F=9.5°.
答:∠F的度数为9.5°.
18.证明:(1)∵∠A=120°,∠ABC=60°,
∴∠A+∠ABC=180°.
∴AD∥BC;
(2)∵AD∥BC,
∴∠1=∠DBC.
∵BD⊥DC,EF⊥DC,
∴∠BDF=90°,∠EFC=90°.
∴∠BDF=∠EFC=90°.
∴BD∥EF.
∴∠2=∠DBC.
∴∠1=∠2.
19.证明:(1)∵∠CDG=∠B,
∴DG∥AB,
∴∠1=∠BAD,
∵∠1+∠FEA=180°,
∴∠BAD+∠FEA=180°,
∴EH∥AD;
(2)由(1)得:∠1=∠BAD,EH∥AD,
∴∠1=∠H,
∴∠BAD=∠H.
20.解:(1)如图1,过点G作GH∥AB,
∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵GM⊥GN,
∴∠MGN=∠MGH+∠HGN=∠AMG+∠CNG=90°;
答:∠AMG+∠CNG的度数为90°;
(2)如图2,过过点G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=40°,
∴∠MGK=∠BMG=40°,
∵MG平分∠BMP,
∴∠GMP=∠BMG=40°,
∴∠BMP=80°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=40°+α,∠MPN=80°﹣α,
∴∠MGN+∠MPN=40°+α+80°﹣α=120°.
21.(1)证明:过点C作CM∥AB,如图1,
∴∠ABC=∠BCM,
∵AB∥ED,
∴∠CDE=∠DCM,
∵∠BCM=∠BCD+∠DCM,
∴∠ABC=∠BCD+∠CDE;
(2)解:∠ABC﹣∠F=90°,理由:
过点C作CN∥AB,如图2,
∴∠ABC=∠BCN,
∵AB∥ED,
∴CN∥EF,
∴∠F=∠FCN,
∵∠BCN﹣∠BCF+∠FCN,
∴∠ABC=∠BCF+∠F,
∵CF⊥BC,
∴∠BCF=90°,
∴∠ABC=90°+∠F,
即∠ABC﹣∠F=90°;
(3)延长HG交EF于点Q,过点G作GP∥EF,如图3,
∴∠BGD=∠CGQ,
∵AB∥DE,
∴∠ABH=∠EQG,
∵GP∥EF,
∴∠EQG=∠PGQ,∠EFG=∠PGF,
∴∠PGQ=∠ABH,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF=∠FGQ,
∵∠FGQ=∠PGQ﹣∠PGF,
∴∠FGQ=∠ABH﹣∠EFG,
∵BH平分∠ABC,FG平分∠CFD,
∴∠ABH=∠ABC,∠EFG=∠CFD,
∴∠FGQ=∠ABC﹣∠CFD=(∠ABC﹣∠CFD),
由(2)可得:∠ABC﹣∠CFD=90°,
∴∠FGQ=×90°=45°,
即∠BGD﹣∠CGF=45°.
一.选择题(共8小题,满分40分)
1.下列说法:
①和为180°且有一条公共边的两个角是邻补角;
②过一点有且只有一条直线与已知直线垂直;
③同位角相等;
④经过直线外一点,有且只有一条直线与这条直线平行;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
2.如图,直线a,b,c被射线l和m所截,则下列关系正确的是( )
A.∠1与∠2是对顶角 B.∠1与∠3是同旁内角
C.∠3与∠4是同位角 D.∠2与∠3是内错角
3.如图,点E在AB的延长线上,下列条件中能够判断AD∥BC的是( )
A.∠1=∠3 B.∠C=∠CBE
C.∠C+∠ABC=180° D.∠2=∠4
4.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA=( )
A.20° B.40° C.50° D.60°
5.已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )
A.30° B.60° C.30°或60° D.60°或120°
6.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
7.如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是( )
A.∠3=∠1+∠2 B.∠2+∠3﹣∠1=90°
C.∠1﹣∠2+∠3=180° D.∠2+∠3﹣∠1=180°
8.如图,某沿湖公路有两次拐弯,如果第一次的拐角∠A=130°,第二次的拐角∠B=160°,第三次的拐角为∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的度数是( )
A.130° B.140° C.150° D.160°
二.填空题(共8小题,满分40分)
9.如图,△DEF是Rt△ABC沿着BC平移得到的.如果AB=8,BE=4,DH=3,则HE= ,阴影部分的面积 .
10.如图所示,将三角尺按如图所示放置在一张长方形纸片上,∠EGF=90°,∠FEG=30°,∠1=130°,则∠BFG的度数是 .
11.如图,直线m∥n.若∠1=40°,∠2=30°,则∠3的大小为 度.
12.已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED= °.
13.如图,AB∥CD,∠ABE=60°,∠E=12°,则∠D= 度.
14.如图,某酒店重新装修后,准备在大厅主楼梯上铺设红色地毯.已知这种地毯每平方米售价160元,主楼梯道宽2.5m,其侧面如图所示,则购买地毯至少需要 元.
15.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=110°,则∠2= .
16.如图,AB∥CD,AD与BC相交于点F,BE平分∠ABC,DE平分∠ADC,∠AFB=96°,则∠BED的度数为 度.
三.解答题(共5小题,满分40分)
17.如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°.
(1)求∠DEF的度数;
(2)求∠F的度数.
18.如图:已知,∠A=120°,∠ABC=60°,BD⊥DC于点D,EF⊥DC于点F,
求证:(1)AD∥BC;
(2)∠1=∠2.
19.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
20.综合探究:
已知,AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=40°,求∠MGN+∠MPN的度数.
21.已知,AB∥DE,点C在AB上方,连接BC、CD.
(1)如图1,求证:∠BCD+∠CDE=∠ABC;
(2)如图2,过点C作CF⊥BC交ED的延长线于点F,探究∠ABC和∠F之间的数量关系;
(3)如图3,在(2)的条件下,∠CFD的平分线交CD于点G,连接GB并延长至点H,若BH平分∠ABC,求∠BGD﹣∠CGF的值.
参考答案
一.选择题(共8小题,满分40分)
1.解:①两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角,原说法错误,不符合题意;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;原说法错误,不符合题意;
③两直线平行,同位角相等;原说法错误,不符合题意;
④经过直线外一点,有且只有一条直线与这条直线平行;原说法正确,符合题意;
其中正确的有1个,
故选:B.
2.解:A、∠1与∠2不是对顶角,原说法错误,故此选项不符合题意;
B、∠1与∠3不是同旁内角,原说法错误,故此选项不符合题意;
C、∠3与∠4是同位角,原说法错误,故此选项不符合题意;
D、∠2与∠3不是内错角,原说法错误,故此选项不符合题意;
故选:C.
3.解:由∠2=∠4,可得AD∥CB;
由∠1=∠3或∠C=∠CBE或∠C+∠ABC=180°,可得AB∥DC;
故选:D.
4.解:由图可得,∠AEF=50°,
又∵DC∥EF,
∴∠BAC=50°,
∵∠B=30°,
∴∠BDA=50°﹣30°=20°,
故选:A.
5.解:如图1,
∵a∥b,
∴∠1=∠α,
∵c∥d,
∴∠β=∠1=∠α=60°;
如图(2),
∵a∥b,
∴∠α+∠2=180°,
∵c∥d,
∴∠2=∠β,
∴∠β+∠α=180°,
∵∠α=60°,
∴∠β=120°.
综上,∠β=60°或120°.
故选:D.
6.解:如图,过点B作BD∥a,
∴∠ABD=∠1=22°,
∵a∥b,
∴BD∥b,
∴∠2=∠DBC=∠ABC﹣∠ABD=60°﹣22°=38°.
故选:A.
7.解:∵l1∥l2∥l3,
∴∠1=∠2+∠4,∠4+∠3=180°,
∴∠1﹣∠2+∠3=180°,
故选:C.
8.解:过点B作BE∥AD,
∵AD∥CF,
∴BE∥AD∥CF,
∴∠ABE=∠A=130°,∠EBC+∠C=180°,
∵∠ABC=160°,∠ABE+∠EBC=∠ABC,
∴∠EBC=30°,
∴∠C=150°.
故选:C.
二.填空题(共8小题,满分40分)
9.解:∵Rt△ABC沿BC方向平移得到Rt△DEF,
∴AB=DE=8,S△ABC=S△DEF,
∴阴影部分面积=梯形ABEH的面积,
∵DH=3,
∴EH=8﹣3=5,
∴阴影部分面积=×(5+8)×4=26.
故答案为5,26.
10.解:∵AD∥BC,∠1=130°,
∴∠BFE=180°﹣∠1=50°,
又∵∠EGF=90°,∠FEG=30°,
∴∠EFG=60°,
∴∠BFG=50°+60°=110°,
故答案为:110°.
11.解:如图,
∵m∥n.∠1=40°,
∴∠4=∠1=40°,
∵∠3是图中三角形的外角,∠2=30°,
∴∠3=∠2+∠4=70°.
故答案为:70.
12.解:如图:过E作EF∥AB,则AB∥EF∥CD,
∵∠A=130°,
∴∠1=180°﹣130°=50°,
∵∠D=25°,
∴∠2=∠D=25°,
∴∠AED=50°+25°=75°,
故答案为:75.
13.解:过点E作EH∥AB,如图,
∵EH∥AB,
∴∠HEB+∠ABE=180°.
∵∠ABE=60°,
∴∠HEB=120°.
∴∠HED=∠HEB+∠FED=120°+12°=132°.
∵EH∥AB,AB∥CD,
∴HE∥CD.
∴∠HED+∠D=180°.
∴∠D=180°﹣132°=48°.
故答案为:48.
14.解:由题意得:
2.7+5.3=8(m),
8×2.5×160=3200(元),
∴购买地毯至少需要3200元,
故答案为:3200.
15.解:如图,过点C作CH∥AB,
则∠ABC+∠BCH=180°,
∵∠ABC+∠C+∠CDE=360°,即∠ABC+∠BCH+∠DCH+∠CDE=360°,
∴∠DCH+∠CDE=180°,
∴CH∥DE,
∴AB∥DE,
∴∠DGF=∠1=110°,
∴∠2=180°﹣110°=70°,
故答案为:70°.
16.解:如图,过点E作EP∥AB,
∵AB∥CD,
∴AB∥CD∥EP,
∴∠ABE=∠BEP,∠CDE=∠DEP,∠ABC=∠BCD,
∵∠ABC+∠BAD+∠AFB=180°,
∴∠ABC+∠BAD=180°﹣∠AFB=84°,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC,∠CDE=∠ADC,
∴∠ABE+∠CDE=(∠ABC+∠BAD)=42°,
∴∠BED=∠BEP+∠DEP=∠ABE+∠CDE)=42°,
故答案为:42.
三.解答题(共5小题,满分40分)
17.解:(1)∵AB∥CD,∠CDE=119°,
∴∠CDE=∠BED=119°,
∵EF平分∠BED,
∴∠DEF=∠BED=59.5°;
答:∠DEF的度数为59.5°.
(2)∵∠AGF=130°,
∴∠FGB=50°,
由(1)知,∠DEF=59.5°,
∵EF平分∠BED,
∴∠DEF=∠BEF=59.5°,
又∵∠BEF=∠FGB+∠F,
∴∠F=9.5°.
答:∠F的度数为9.5°.
18.证明:(1)∵∠A=120°,∠ABC=60°,
∴∠A+∠ABC=180°.
∴AD∥BC;
(2)∵AD∥BC,
∴∠1=∠DBC.
∵BD⊥DC,EF⊥DC,
∴∠BDF=90°,∠EFC=90°.
∴∠BDF=∠EFC=90°.
∴BD∥EF.
∴∠2=∠DBC.
∴∠1=∠2.
19.证明:(1)∵∠CDG=∠B,
∴DG∥AB,
∴∠1=∠BAD,
∵∠1+∠FEA=180°,
∴∠BAD+∠FEA=180°,
∴EH∥AD;
(2)由(1)得:∠1=∠BAD,EH∥AD,
∴∠1=∠H,
∴∠BAD=∠H.
20.解:(1)如图1,过点G作GH∥AB,
∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵GM⊥GN,
∴∠MGN=∠MGH+∠HGN=∠AMG+∠CNG=90°;
答:∠AMG+∠CNG的度数为90°;
(2)如图2,过过点G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=40°,
∴∠MGK=∠BMG=40°,
∵MG平分∠BMP,
∴∠GMP=∠BMG=40°,
∴∠BMP=80°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=40°+α,∠MPN=80°﹣α,
∴∠MGN+∠MPN=40°+α+80°﹣α=120°.
21.(1)证明:过点C作CM∥AB,如图1,
∴∠ABC=∠BCM,
∵AB∥ED,
∴∠CDE=∠DCM,
∵∠BCM=∠BCD+∠DCM,
∴∠ABC=∠BCD+∠CDE;
(2)解:∠ABC﹣∠F=90°,理由:
过点C作CN∥AB,如图2,
∴∠ABC=∠BCN,
∵AB∥ED,
∴CN∥EF,
∴∠F=∠FCN,
∵∠BCN﹣∠BCF+∠FCN,
∴∠ABC=∠BCF+∠F,
∵CF⊥BC,
∴∠BCF=90°,
∴∠ABC=90°+∠F,
即∠ABC﹣∠F=90°;
(3)延长HG交EF于点Q,过点G作GP∥EF,如图3,
∴∠BGD=∠CGQ,
∵AB∥DE,
∴∠ABH=∠EQG,
∵GP∥EF,
∴∠EQG=∠PGQ,∠EFG=∠PGF,
∴∠PGQ=∠ABH,
∴∠BGD﹣∠CGF=∠CGQ﹣∠CGF=∠FGQ,
∵∠FGQ=∠PGQ﹣∠PGF,
∴∠FGQ=∠ABH﹣∠EFG,
∵BH平分∠ABC,FG平分∠CFD,
∴∠ABH=∠ABC,∠EFG=∠CFD,
∴∠FGQ=∠ABC﹣∠CFD=(∠ABC﹣∠CFD),
由(2)可得:∠ABC﹣∠CFD=90°,
∴∠FGQ=×90°=45°,
即∠BGD﹣∠CGF=45°.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
